今天分享的題目來源于 LeetCode 上的劍指 Offer 系列面試題07. 重建二叉樹,近半年在微軟面試環(huán)節(jié)出現(xiàn)過 2 次,屬于中高難度的算法題!
一、題目描述
輸入某二叉樹的前序遍歷和中序遍歷的結(jié)果,請重建該二叉樹。假設(shè)輸入的前序遍歷和中序遍歷的結(jié)果中都不含重復(fù)的數(shù)字。
例如,給出
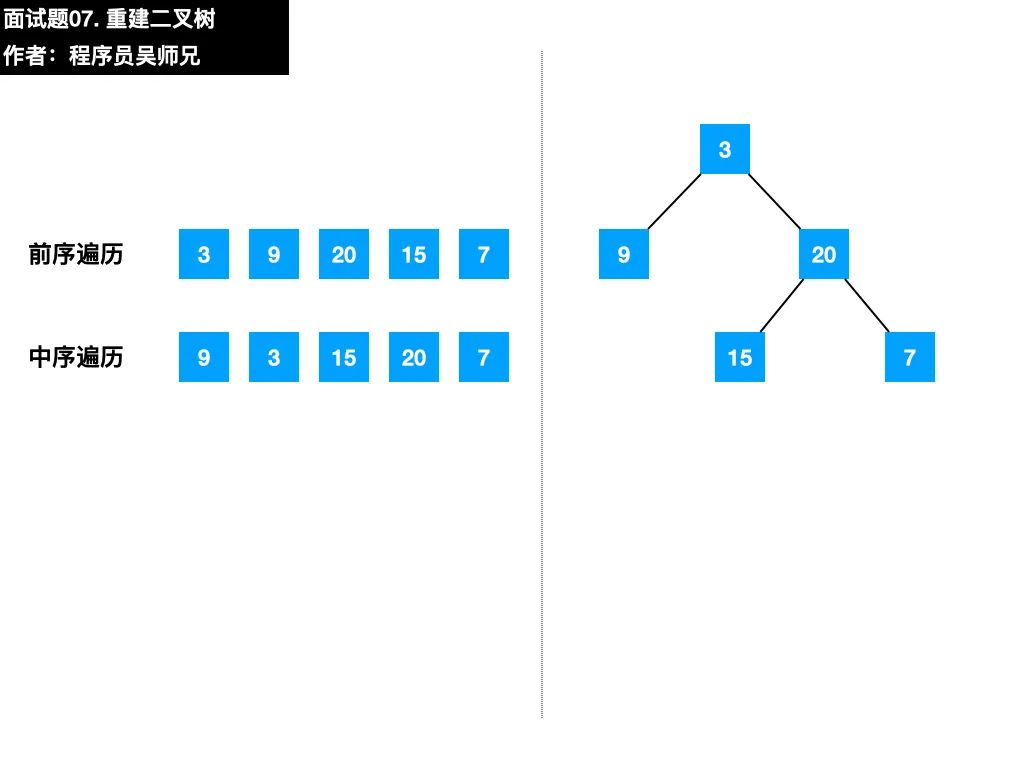
前序遍歷preorder=[3,9,20,15,7] 中序遍歷inorder=[9,3,15,20,7]
返回如下的二叉樹:
3 / 920 / 157
限制:
0 <= 節(jié)點個數(shù) <= 5000
二、題目解析
首先,我們先來復(fù)習(xí)一下前序遍歷、中序遍歷。(在下方的視頻中分布講解)
前序遍歷
二叉樹的前序遍歷順序是:根節(jié)點、左子樹、右子樹,每個子樹的遍歷順序同樣滿足前序遍歷順序。
中序遍歷
二叉樹的中序遍歷順序是:左子樹、根節(jié)點、右子樹,每個子樹的遍歷順序同樣滿足中序遍歷順序。
復(fù)習(xí)過后,我們可以得出以下結(jié)論:
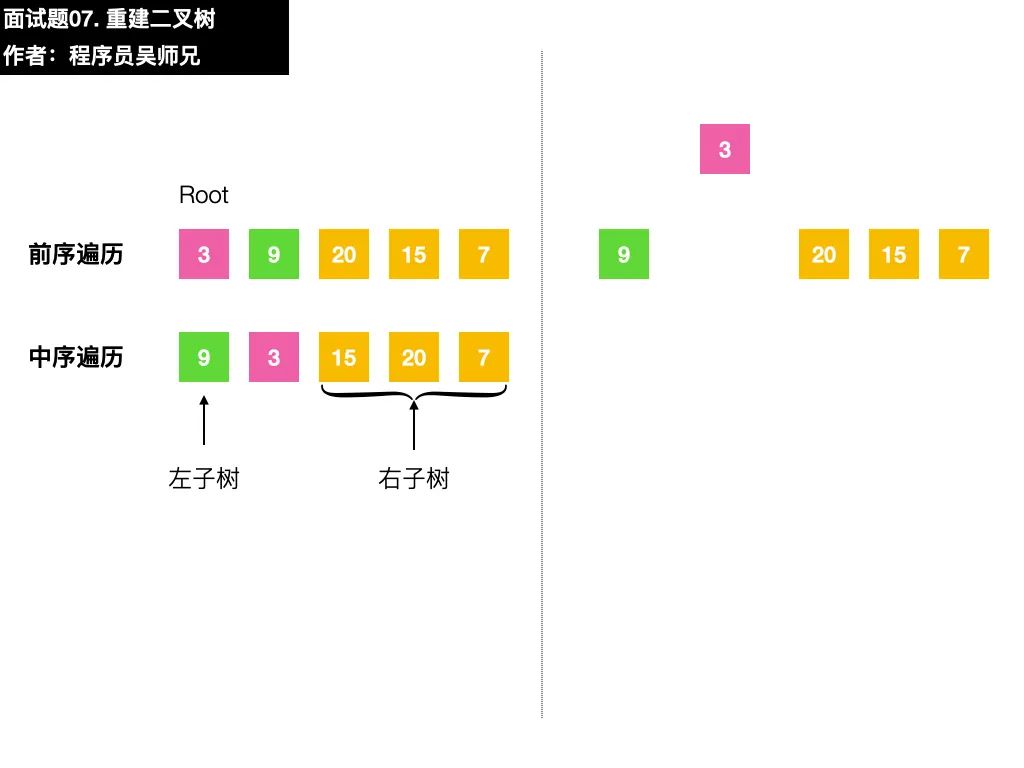
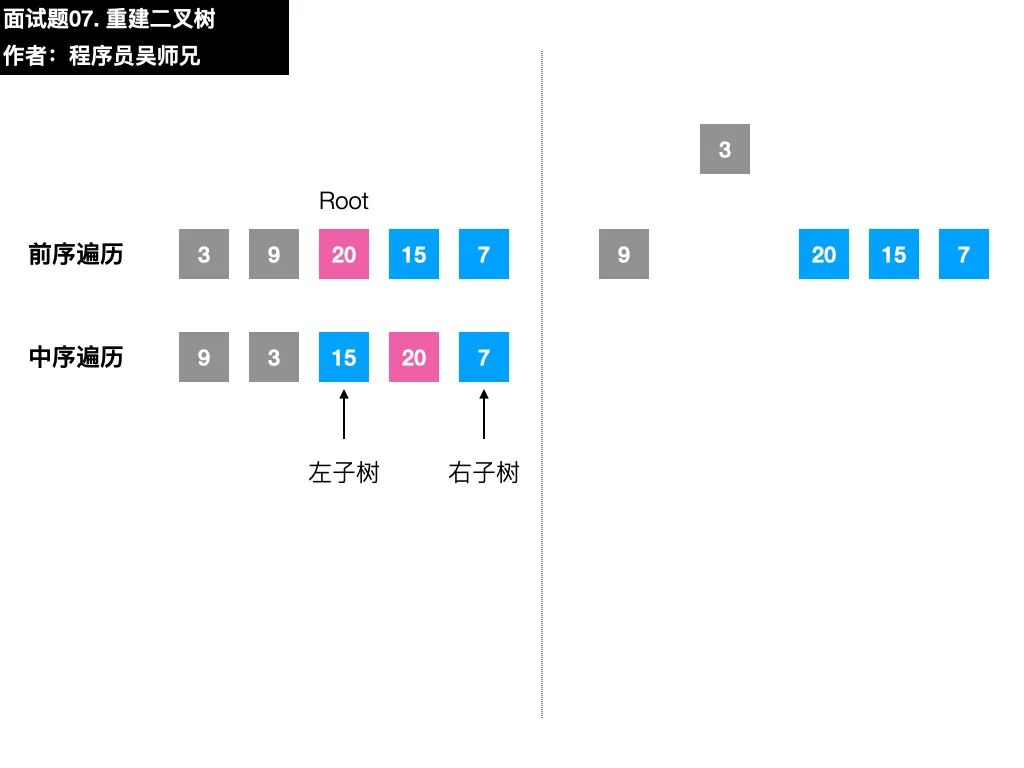
在二叉樹的前序遍歷序列中,第一個數(shù)字總是樹的根結(jié)點的值;
在二叉樹的中序遍歷序列中,根結(jié)點的值在序列的中間,左子樹的結(jié)點的值位于根結(jié)點的值的左邊,而右子樹的結(jié)點的值位于根結(jié)點的值的右邊
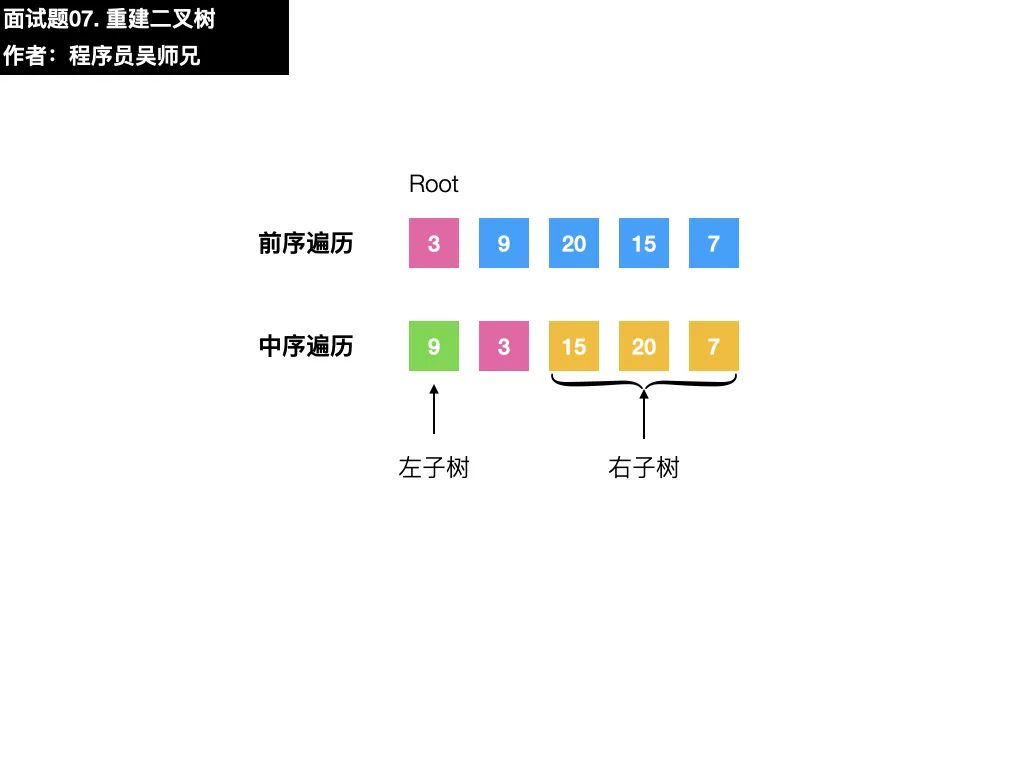
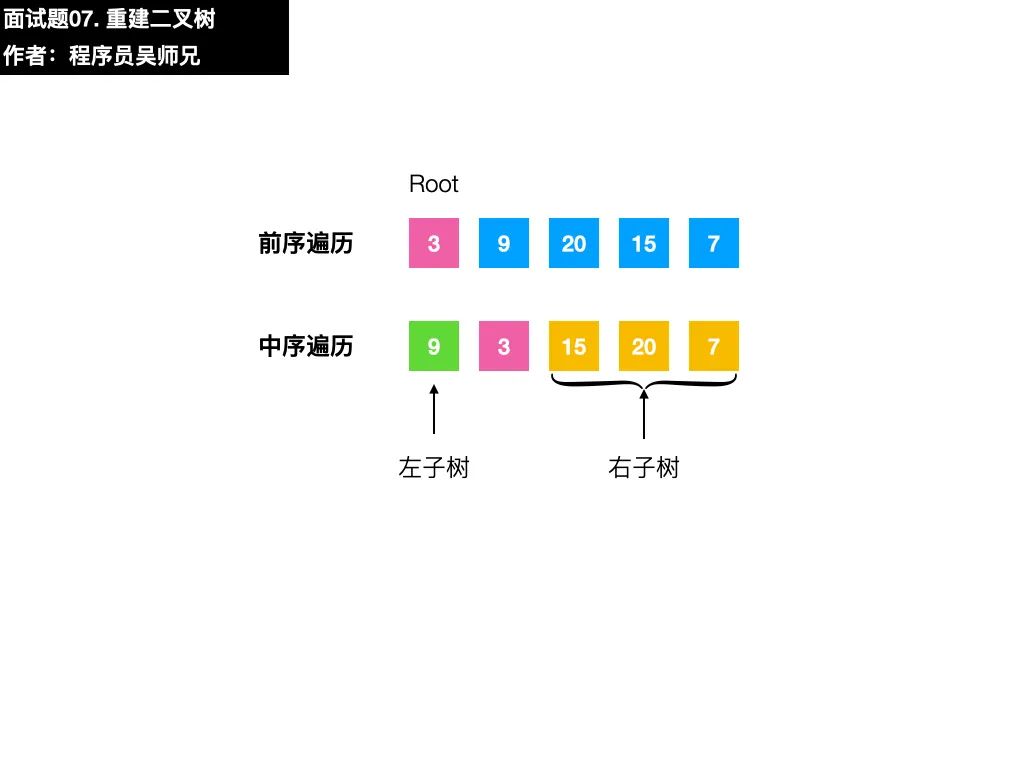
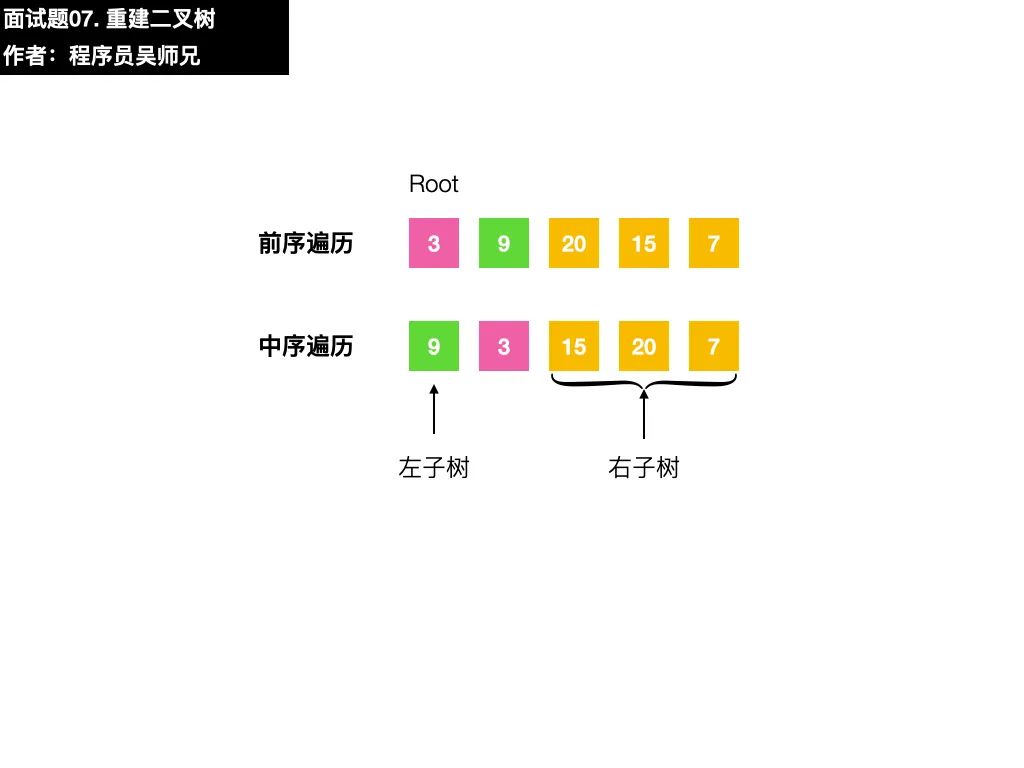
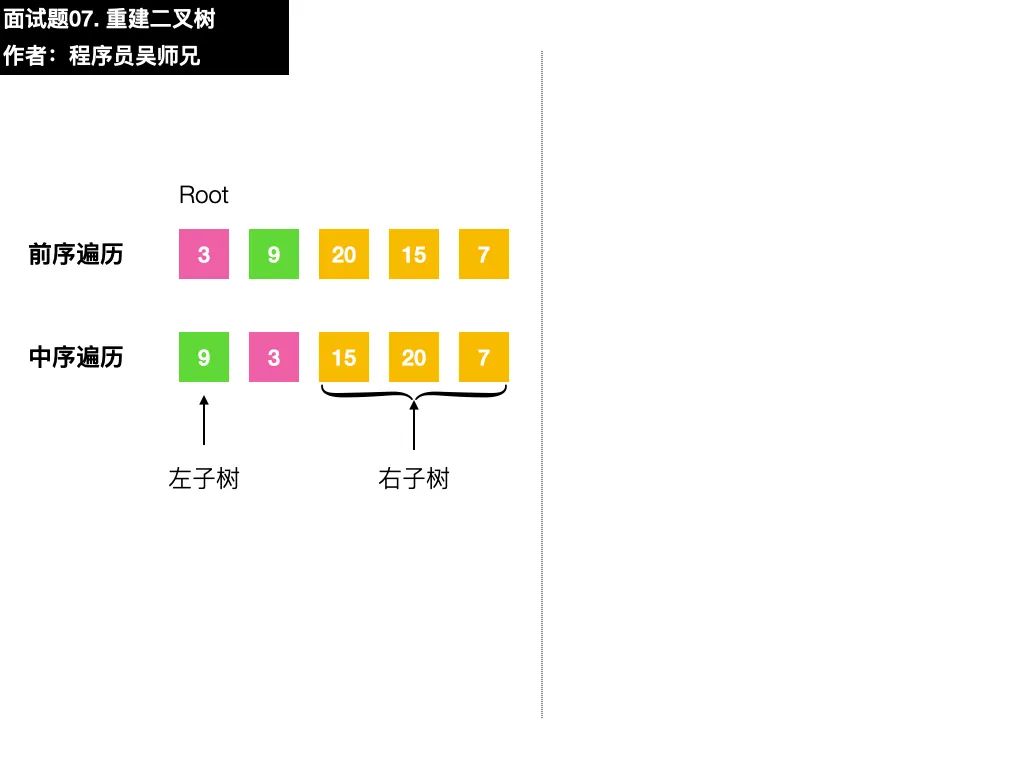
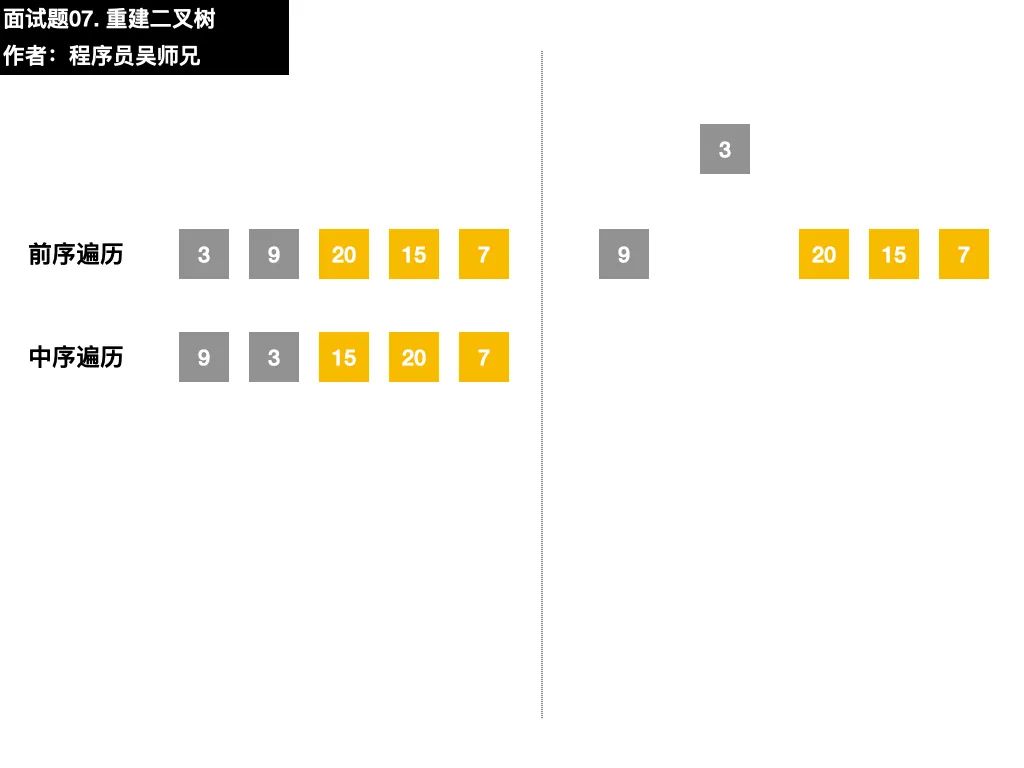
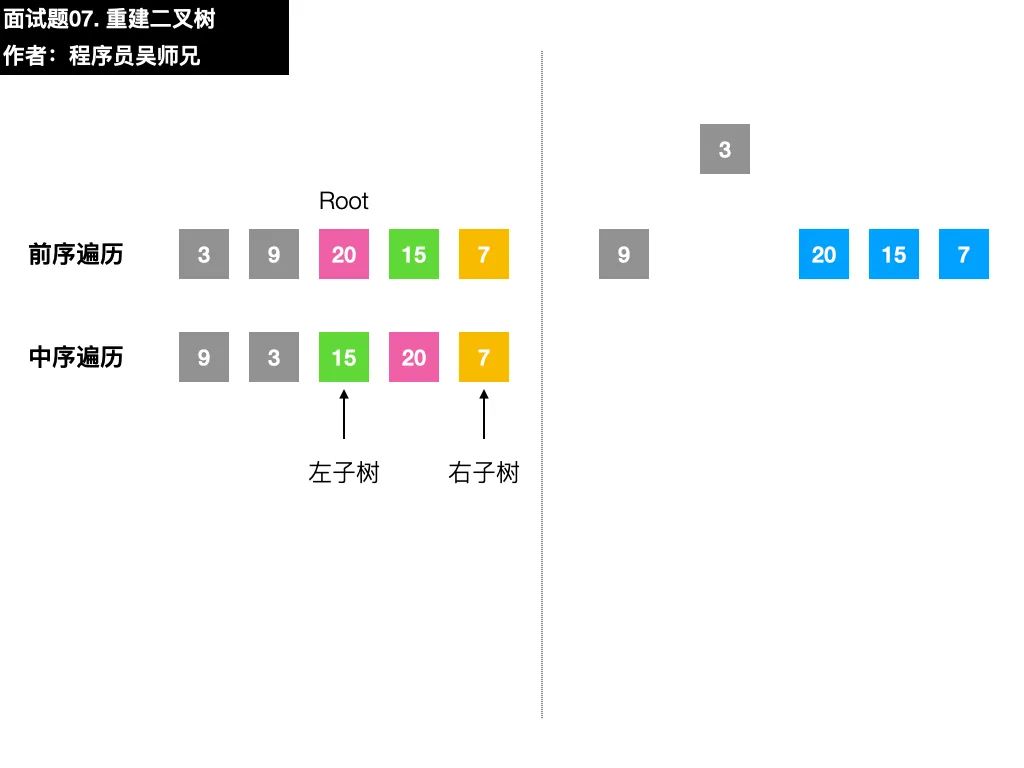
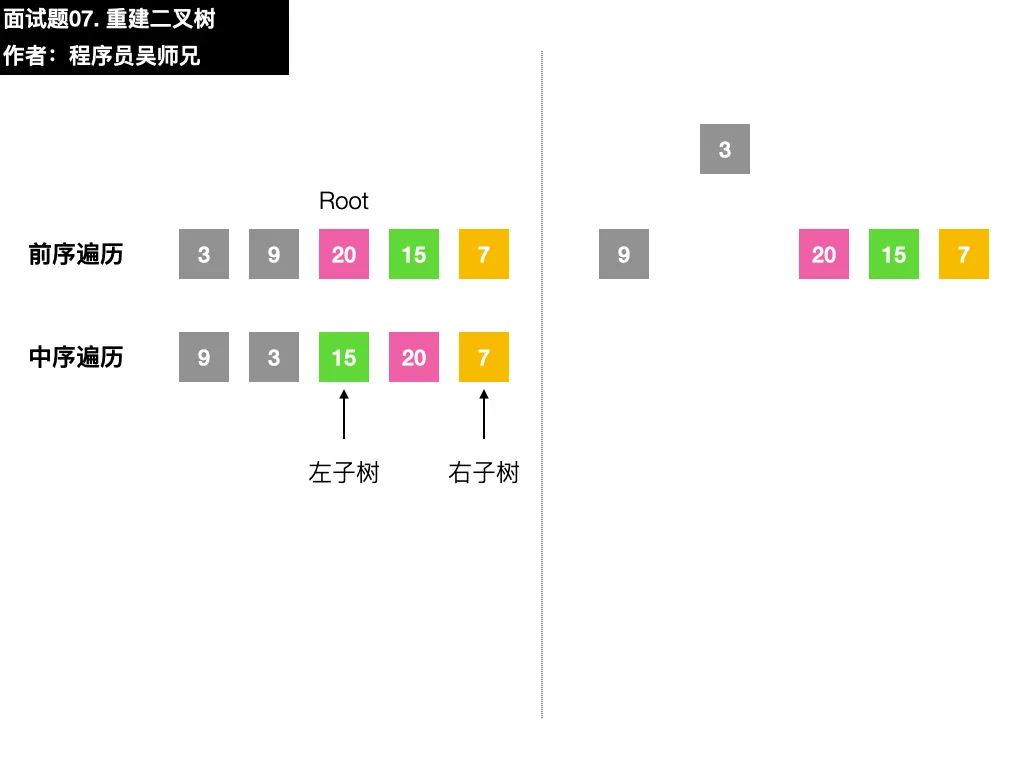
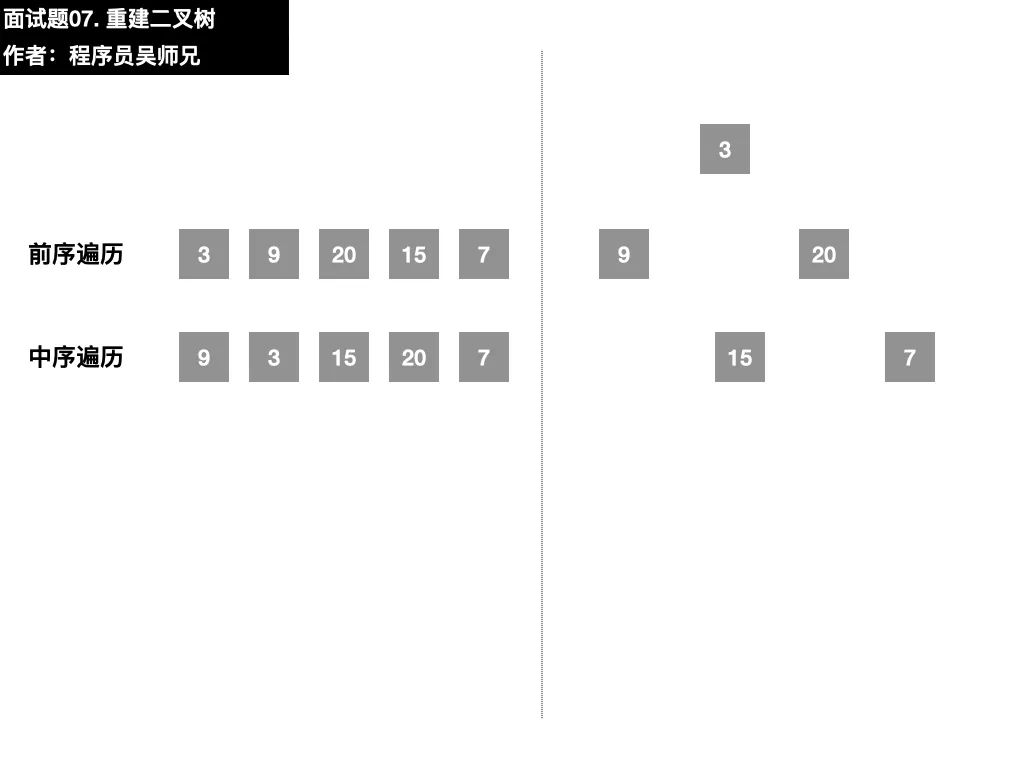
以本題的序列為例,前序遍歷序列的第一個數(shù)字 3 就是根結(jié)點的值,在中序遍歷序列,找到根結(jié)點值的位置。根據(jù)中序遍歷特點,在根結(jié)點的值 3前面的數(shù)字都是左子樹結(jié)點的值,在根結(jié)點的值 3后面的數(shù)字都是右子樹結(jié)點的值。
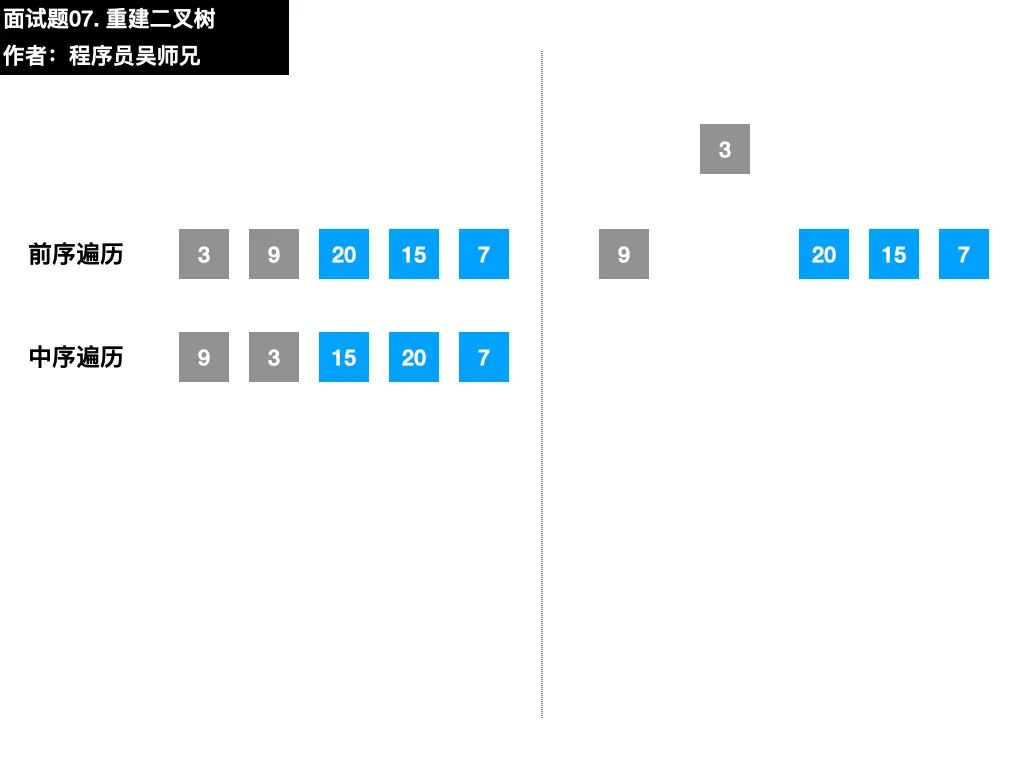
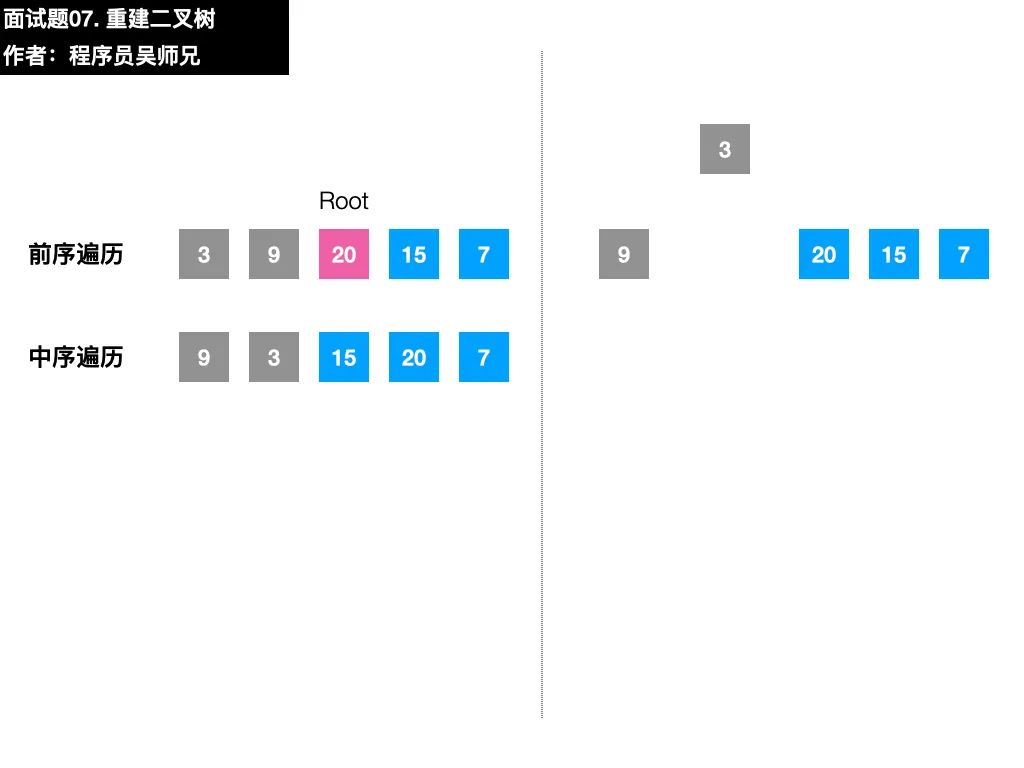
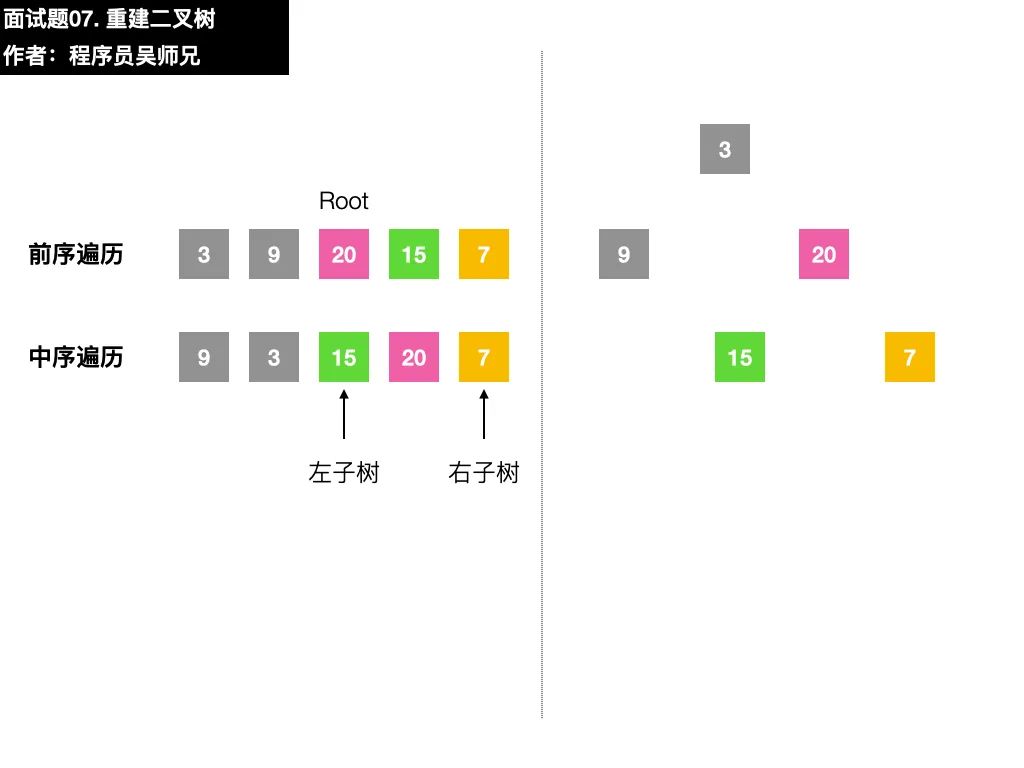
二叉樹很重要的一個性質(zhì)是遞歸,在找到了左子樹、右子樹的前序遍歷序列和中序遍歷序列后,我們可以按照同樣的方法去確定子左子樹和子右子樹的構(gòu)建。
具體的代碼編寫思路如下(來源于 Krahets's Blog):
遞推參數(shù):前序遍歷中根節(jié)點的索引pre_root_idx、中序遍歷左邊界in_left_idx、中序遍歷右邊界in_right_idx。
終止條件:當(dāng)in_left_idx > in_right_idx,子樹中序遍歷為空,說明已經(jīng)越過葉子節(jié)點,此時返回 null 。
遞推工作:
建立根節(jié)點 root :值為前序遍歷中索引為pre_root_idx的節(jié)點值。
搜索根節(jié)點 root 在中序遍歷的索引 i :為了提升搜索效率,本題解使用哈希表map預(yù)存儲中序遍歷的值與索引的映射關(guān)系,每次搜索的時間復(fù)雜度為 O(1)。
構(gòu)建根節(jié)點root的左子樹和右子樹:通過調(diào)用 recursive()方法開啟下一層遞歸。
左子樹:根節(jié)點索引為 pre_root_idx + 1 ,中序遍歷的左右邊界分別為 in_left_idx 和 i - 1。
右子樹:根節(jié)點索引為 i - in_left_idx + pre_root_idx + 1(即:根節(jié)點索引 + 左子樹長度 + 1),中序遍歷的左右邊界分別為 i + 1 和 in_right_idx。
返回值:返回root,含義是當(dāng)前遞歸層級建立的根節(jié)點root為上一遞歸層級的根節(jié)點的左或右子節(jié)點。
三、動畫描述
四、圖片描述





五、參考代碼
classSolution{ //在中序序列中查找與前序序列首結(jié)點相同元素的時候,如果使用while循環(huán)去一個個找效率很慢 //這里我們借助數(shù)據(jù)結(jié)構(gòu)HashMap來輔助查找,在開始遞歸之前把所有的中序序列的元素和它們所在的下標(biāo)存到一個map中,這樣查找的時間復(fù)雜度是O(logn) HashMap
這段代碼的一個難點就是root.left與root.right,我這里抽離出來詳細(xì)解釋一下。
1、root.left

2、root.right
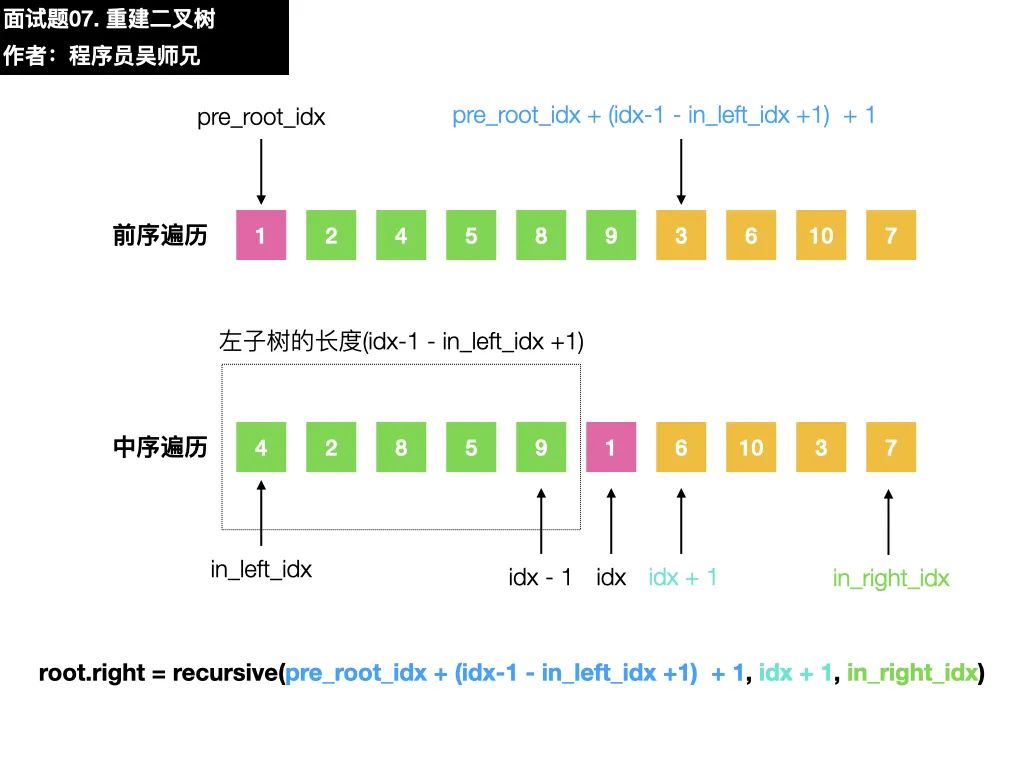
六、復(fù)雜度分析
時間復(fù)雜度
時間復(fù)雜度為 O(N)。
空間復(fù)雜度
空間復(fù)雜度為 O(N)。
七、相關(guān)標(biāo)簽
樹
遞歸
哈希表
八、參考來源
1、https://leetcode-cn.com/problems/zhong-jian-er-cha-shu-lcof/solution/mian-shi-ti-07-zhong-jian-er-cha-shu-di-gui-fa-qin/ 題解區(qū)
2、https://krahets.gitee.io/views/sword-for-offer/2020-02-24-sword-for-offer-07.html
-
數(shù)字
+關(guān)注
關(guān)注
1文章
1698瀏覽量
51948 -
二叉樹
+關(guān)注
關(guān)注
0文章
74瀏覽量
12650
原文標(biāo)題:面試字節(jié)跳動時,我竟然遇到了原題……
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
每周推薦!硬件設(shè)計指南+無刷電機(jī)原理圖大全+工程師面試題庫匯總
硬件工程師或研發(fā)類筆試面試題庫匯總
最全的硬件工程師筆試試題集
【硬件方向】名企面試筆試真題:大疆創(chuàng)新校園招聘筆試題
硬件工程師面試/筆試經(jīng)典 100 題

硬件工程師面試必看試題(經(jīng)典)
請問有沒有辦法修改live系統(tǒng)上的設(shè)備樹?
【面試題】人工智能工程師高頻面試題匯總:概率論與統(tǒng)計篇(題目+答案)
飛凌嵌入式ElfBoard ELF 1板卡-初識設(shè)備樹之設(shè)備樹組成和結(jié)構(gòu)
【面試題】人工智能工程師高頻面試題匯總:機(jī)器學(xué)習(xí)深化篇(題目+答案)
【面試題】人工智能工程師高頻面試題匯總:Transformer篇(題目+答案)
人工智能工程師高頻面試題匯總——機(jī)器學(xué)習(xí)篇

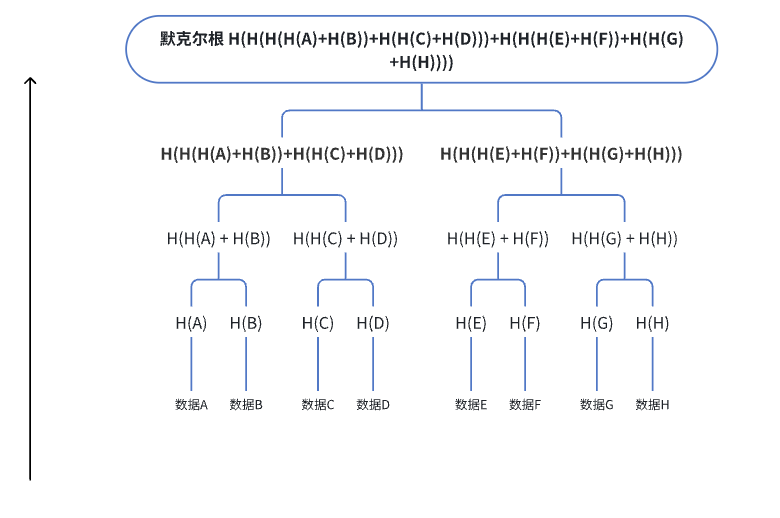
什么是默克爾樹(Merkle Tree)?如何計算默克爾根?



















評論