二進制:二進制數據是用0和1兩個數碼來表示的數。它的基數為2,進位規則是“逢二進一”,借位規則是“借一當二”。計算機中的二進制則是一個非常微小的開關,用“開”來表示1,“關”來表示0。
二進制的計算由計算機內的門電路進行,門電路可以有一個或多個輸入端,但只有一個輸出端。
原碼(true form)是一種計算機中對數字的二進制定點表示方法。原碼表示法在數值前面增加了一位符號位(即最高位為符號位):正數該位為0,負數該位為1(0有兩種表示:+0和-0),其余位表示數值的大小。
簡單直觀;例如,我們用8位二進制表示一個數,+11的原碼為00001011,-11的原碼就是10001011
反碼:規定 正數的反碼與原碼相同。負數:負數的反碼,符號位為“1”,數值部分按位取反。
補碼:規定 正數:正數的補碼和原碼相同。負數:負數的補碼則是符號位為“1”。并且,這個“1”既是符號位,也是數值位。數值部分按位取反后再在末位(最低位)加1。也就是“反碼+1”。
1、門電路
1.1、定義
門電路:“門”是這樣的一種電路:它規定各個輸入信號之間滿足某種邏輯關系時,才有信號輸出,通常有下列三種門電路:與門、或門、非門(反相器)。從邏輯關系看,門電路的輸入端或輸出端只有兩種狀態,無信號以“0”表示,有信號以“1”表示。也可以這樣規定:低電平為“0”,高電平為“1”。門電路一般配合二級管制做。
1.2、與門
一種基本的門電路,有多個輸入端,一個輸出端。當所有的輸入同時為高電平(邏輯1)時,輸出才為高電平,否則輸出為低電平(邏輯0)。
與門的真值表:
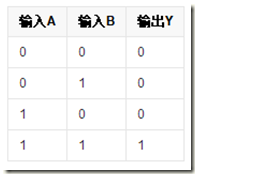
與門的二級管實現:
以二極管實現為例,與門的實現原理為:
如圖:為二極管與門電路,Vcc = 5v,R1 = 3KΩ, 假設3v及以上代表高電平,0.7及以下代表低電平,
下面根據圖中情況具體分析一下,
1. Ua=Ub=0v時,D1,D2正向偏置,兩個二極管均會導通,此時Uo為電位為0.7v.,輸出為低電平
2.當Ua,Ub一高一低時,不妨假設Ua = 3v,Ub = 0v,這時我們不妨先從D2開始分析,
D2會導通,導通后D2壓降將會被限制在0.7v,那么D1由于右邊是0.7v左邊是3v所以會反向偏置而截止,因此最后Uo為0.7v低電平輸出,這里也可以從D1開始分析,如果D1導通,那么Uo應當為3.7v,
此時D2將導通,那么D2導通,壓降又會變回0.7,最終狀態Uo仍然是0.7v.輸出低電平,此時D1馬上截止。
3. Va=Vb=3v,這個情況很好理解, D1,D2都會正偏,Uy被限定在3.7V.
總結(借用個定義):通常二極管導通之后,如果其陰極電位是不變的,那么就把它的陽極電位固定在比陰極高0.7V的電位上;如果其陽極電位是不變的,那么就把它的陰極電位固定在比陽極低0.7V的電位上,人們把導通后二極管的這種作用叫做鉗位。(特別說明:壓差大的二極管先導通,先鉗位,先導通的二極管具有電路控制權)
1.3、或門
一種基本的門電路:或門有多個輸入端,一個輸出端,只要輸入中有一個為高電平時(邏輯“1”),輸出就為高電平(邏輯“1”);只有當所有的輸入全為低電平(邏輯“0”)時,輸出才為低電平(邏輯“0”)
或門的真值表:
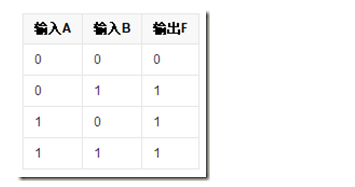
或門的二級管實現:
如圖,這里取Vss=0v,不取-10v
1、當Ua=Ub=0v時,D1,D2都截至,那么y點為0v.
2、當Ua=3v,Ub=0v時,此時D1導通,Uy=3-0.7=2.3v,D2則截至
同理Ua=0v,Ub=3v時,D2導通,D1截至,Uy=2.3v.
3、當Ua=Ub=3v時,此時D1,D2都導通,Uy=3-0.7=2.3v.
1.4、非門
一種基本的門電路:非門有一個輸入和一個輸出端。當其輸入端為高電平(邏輯1)時輸出端為低電平(邏輯0),當其輸入端為低電平時輸出端為高電平。也就是說,輸入端和輸出端的電平狀態總是反相的。
非門的真值表:
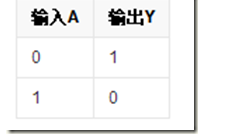
三級管非門的實現:
晶體管“非”門電路不同于放大電路,管子的工作狀態或從截止轉為飽和,或從飽和轉為截止。“非”門電路只有一個輸入端A,
當A為“1”(設其電位為3V)時,晶體管飽和,其集電極,即輸出端Y為“0”(其電位在零伏附近);
當A為“0”時,晶體管截止,輸出端Y為“1”(其電位近似等于)。所以“非”門電路也稱為反相器。加負電源是為了使晶體管可靠截止。
圖中,是“非”門的門電阻,其作用是通過它向輸出端提供電壓。T飽和,上產生很大的壓降,使集電極電位幾乎與發射極的電位相等;截止時,通過加到集電極上,使集電極電壓等于。是輸入電阻,通過它給T加正向偏置電流,即輸入信號。是反偏電阻,通過它給T加反向偏置電流。這兩個電阻配合得當,才可以使輸入“1”時T飽和導通,輸入“0”時T可靠截止。
1.5、其他門電路
其他門電路如:與非門、或非門、異或門等都是以上三個基本門電路組合而來。
異或門:若兩個輸入的電平相異,則輸出為高電平1;若兩個輸入的電平相同,則輸出為低電平0。亦即,如果兩個輸入不同,則異或門輸出高電平1。
2、加減乘除計算
2.1、加法運算
加法器:對于1位的二進制加法,相關的有五個的量:1,被加數A,2,被加數B,3,前一位的進位CIN,4,此位二數相加的和S,5,此位二數相加產生的進位COUT。前三個量為輸入量,后兩個量為輸出量,五個量均為1位。
計算機的加法器都是以上面的逐位進位加法器優化而來,不再深入探索,有興趣的可自行查找資料。
加法器原理就是用門電路實現二進制的相加運算。
2.2、減法運算
在計算機中,加法和減法其實是一種運算,原因在于計算機表示負數的方法。
計算機中的數據存儲時都會轉化成相應的二進制補碼,補碼有三個特性:
1、一個負整數(或原碼)與其補數(或補碼)相加,和為模。
2、對一個整數的補碼再求補碼,等于該整數自身。
3、補碼的正零與負零表示方法相同。
模的定義:“模”是指一個計量系統的計數范圍。如時鐘等。計算機也可以看成一個計量機器,它也有一個計量范圍,即都存在一個“模”。例如:
時鐘的計量范圍是0~11,模=12。表示n位的計算機計量范圍是0~2^(n)-1,模=2^(n)。
“模”實質上是計量器產生“溢出”的量,它的值在計量器上表示不出來,計量器上只能表示出模的余數。任何有模的計量器,均可化減法為加法運算。
例如:假設當前時針指向10點,而準確時間是6點,調整時間可有以下兩種撥法:一種是倒撥4小時,即:10-4=6;另一種是順撥8小時:10+8=12+6=6
舉例:
1、如計算機要計算8-3
2、存儲8為:0000 1000 (正數的補碼與原碼相同)
3、存儲-3為:1111 1101 (負數的補碼為符號為定為1,其他位求反碼后加1)
4、8-3 可直接用加法器做加法運算8 + (-3) 二進制可得:0000 0101 轉化為十進制為:5
2.3、乘法運算
我們計算兩個數相乘時一般如下計算:

其實加法器也是模擬這樣的過程,只不過是改為了二進制數而已。計算機通過加法器和適當的移位操作完成了乘法運算。
例子:
1011 X 1001 用十進制表示為 11X9 結果當然為99
以上文章中有很多乘法器的優化,我只講我覺得好理解的一個
一、乘數寄存器四位保存1011。
二、被乘數寄存器四位保存1001。
三、乘積寄存器八位保存乘積,初始0000 0000,乘積寄存器只前四位參與運算,后四位只為記錄。
1、第一次運算取乘數最后一位 得1,乘積寄存器前四位加 被乘數 得 1001 0000
2、乘數寄存器右移一位得:0101 乘積寄存器右移一位得 0100 1000
3、第二次運算重復步驟1、2 得,乘數:0010 乘積:0110 1100
4、如此,乘數有幾位就重復次幾運算,當乘數最后一位為0 時不做加操作,只進行移位。
5、第三次運算得,乘數:0001 乘積: 0011 0110
6、第四次運算得,乘數:0000,四次后整個運算完成,乘積:0110 0011 轉化為十進制為:99
如上步驟中我們可以看出,計算機計算乘法跟我們計算乘法時的步驟一樣,我們用乘數的個十百千們分別與被乘數相乘,然后錯位相加得積,計算積也是把乘數的第一二三四位分別與被乘數相乘(相乘時乘數為1則積為被乘數,乘數為0時則四位全為0所以此時只進行移位操作) 然后用移位操作來模擬錯位相加。
2.4、除法運算
文章里也有很多除法器優化方案,我只以容易理解的說,其原理都是一般。
原理:除法可以變化為減法來算,一個數除以另一個數,可以理解為一個數循環減去另一個數減了幾遍商便是幾,這種方式在十進制里可能實在麻煩,但是在二進制里卻簡單了不少。
如果兩個一位數相除8/3 可理解為8-3-3 = 2,得商為2 余數為2,但在二進制里兩個一位數相除只有兩種可能,一種是我大于你,商得1余數是兩個數相減,另一種是我小于你商是0,余數是我本身;
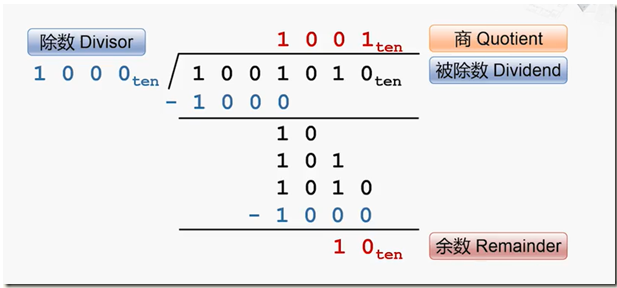
如上計算方式我們十進制時也是常用的,只是我們配合九九乘法口決計算,而二進制里只需要從被除數高位開始逐位與除數相減,減的到此為得1 ,決不會有可以減兩次的可能(即商不可能得2),減不到此位得0;
1、被除數十一位寄存,其實有效數字只占七位、除數四位寄存、商八位寄存,被除數參與運算的只有前四位(因為除數為四位即前四位)
2、被除數:0000 1001 010 除數:1000 商:0000 0000
3、參于運算的值我用紅色標識: (1)被除數左移進入運算位后位補0: 0001 0010 100 除數:1000 減不到商得0 余為0001 商左移《1》為0000 0000
4、(2)被除數左移一位 變為:0010 0101 000 除數:1000 減不到此為得0 余為0010 商左移《2》為0000 0000
5、(3)被除數再左移變為:0100 1010 000 商左移《3》為0000 0000,(4)再左移得:1001 0100 000 此時可以減得 商左移《4》為0000 0001 余數為:0001,被除數被減后變為:0001 0100 000
6、(5)被除數左移變為0010 1000 000 《5》商左移為0000 0010 (6)再左移:0101 0000 000 《6》商左移為0000 0100 (7)再左移:1010 0000 000 此時可以減得 《7》商左移為0000 1001 余數為:0010 被除數被減后變為:0010 0000 000
7、被除數有幾位就移動幾位,商也跟著移動幾位,如上圖標號標識,七次移位后得商為:0000 1001 余數為:0010 后七位舍去,只要參與計算的前四位。轉化為十進制為74/8 = 9 余 2
總結:除法器可以用減法替代除法,因為這樣移位相減,在某一位上最多只能減一次被除數便會小于除數,所以商得1,同理十進制被除數和除數如此移位相減的話在某一位上最多只能減九次,即商最大只能為9。
-
二進制
+關注
關注
2文章
795瀏覽量
41643 -
計算機
+關注
關注
19文章
7488瀏覽量
87854 -
門電路
+關注
關注
7文章
199瀏覽量
40160
發布評論請先 登錄
相關推薦
用AT89S52單片機制作萬年歷外加簡單計算器,主要是加減乘除
labview如何實現加減乘除的混合運算
霧盈FPGA筆記之(三十二)六位四則運算計算器(8)算法實現加減乘除
用Case結構設計一個簡易計算器,僅需要滿足加減乘除即可,但要求加減乘除四個運算符用下拉菜單表示。
用數碼管顯示的簡易計算器(可加減乘除)利用矩陣鍵盤實現,原理圖和程序誰懂啊?大神求教。
伺服電機的選型計算方法相關資料分享
聊聊計算機加法的電路原理和proteus仿真
怎樣去設計一個簡易計算器
使用51單片機設計的可連續運算的加減乘除數碼管顯示計算器程序
大話計算機的PPT演示文稿資料免費下載
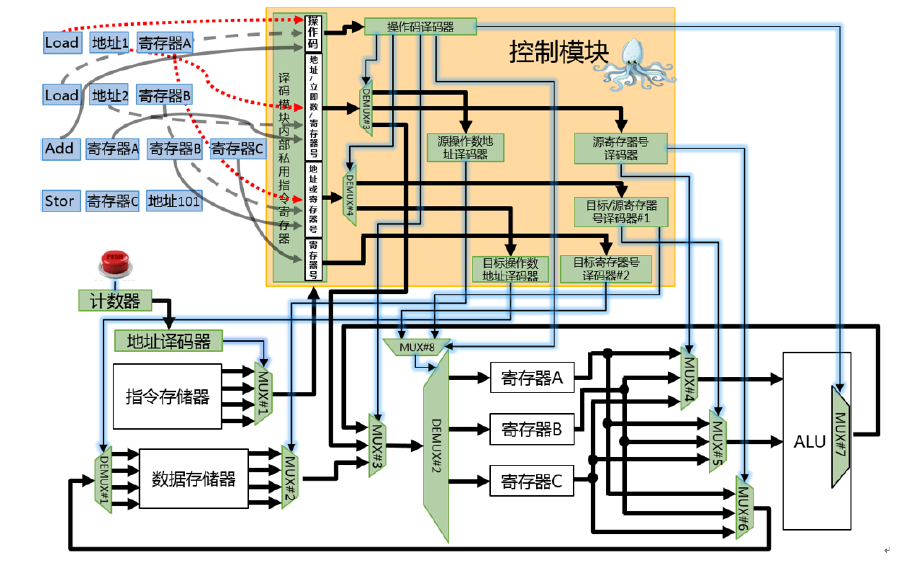




 計算機的門電路和加減乘除計算方法
計算機的門電路和加減乘除計算方法











評論