作者|仿真居工 仿真秀專欄作者

在進行有限元仿真計算時，常常會遇到計算不收斂的問題，而且導(dǎo)致求解不收斂的原因也是多種多樣的，處理起來也是相當?shù)穆闊Ｌ貏e是在利用隱式算法的求解非線性問題時，對靜態(tài)平衡方程進行迭代求解時極易出現(xiàn)計算的不收斂問題，而顯式算法基于動力學(xué)方程，不需要進行平衡迭代，當時間步長足夠小時，一般不存在收斂性問題。無論在哪種算法下出現(xiàn)計算不收斂情況，首先要學(xué)會根據(jù)軟件報錯信息排查不收斂的原因，然后對癥下藥，排除問題。

一：不收斂問題的排查方法

●若剛開始進入模型計算階段就出現(xiàn)不收斂問題，可能原因有：有限元模型網(wǎng)格質(zhì)量欠佳、邊界條件約束不足（出現(xiàn)剛體位移）、接觸設(shè)置不當、重復(fù)導(dǎo)入部件（導(dǎo)致欠約束）、初始載荷過大、初始應(yīng)力導(dǎo)致的材料塑性、由于單位制未統(tǒng)一間接導(dǎo)致剛度過小或載荷過大等原因，根據(jù)提示信息，找出報錯位置進行修改。

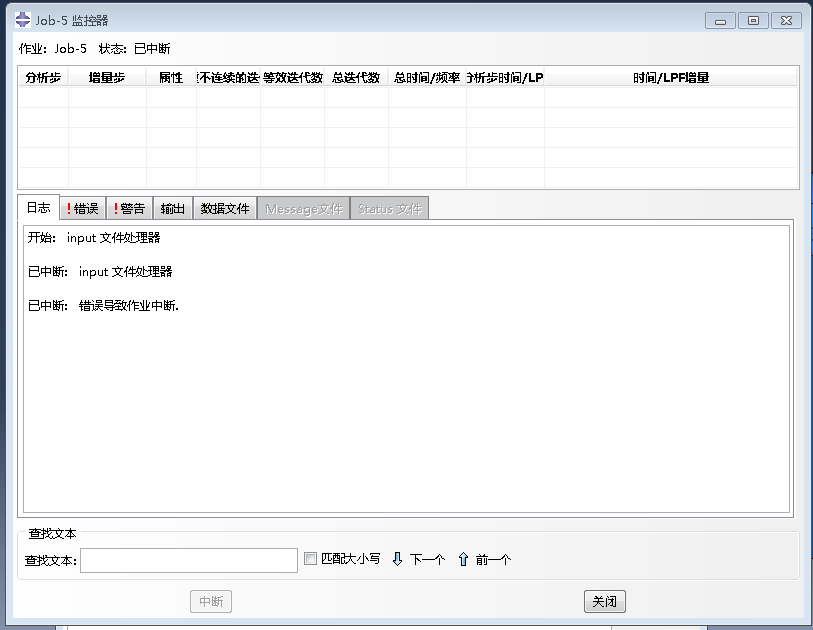
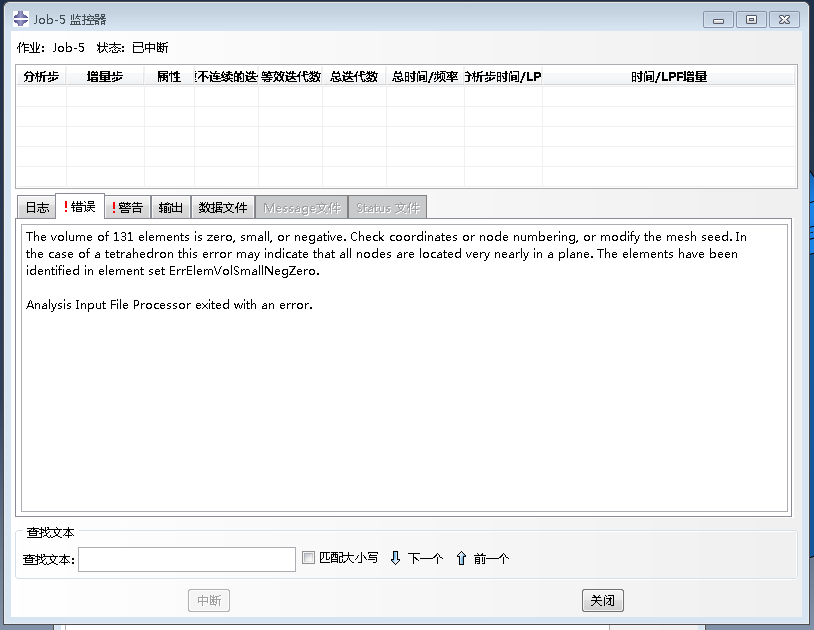
●若在模型計算階段的中后期才出現(xiàn)不收斂的情況，需要根據(jù)已有的計算結(jié)果和模型情況進行判斷。主要排查方向有：材料軟化、失效、屈曲、接觸非線性、溫度或其他場量的驟變等方面。

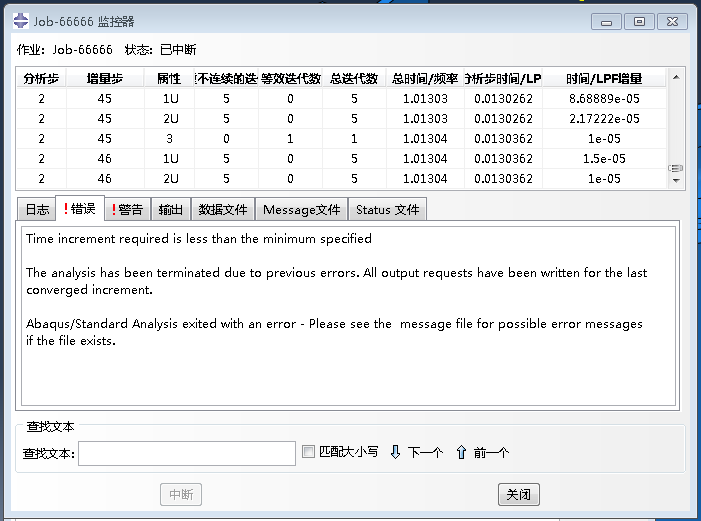
其中最為常見的是隨著加載的進行出現(xiàn)畸變單元而導(dǎo)致終止（例如上圖），一般來講此類情況不歸屬于不收斂問題，而是由于網(wǎng)格畸變導(dǎo)致無法計算單元剛度矩陣，從而無法組裝整體剛度矩陣。這種情況的解決辦法通常需要重新劃分網(wǎng)格，以獲得更高質(zhì)量的網(wǎng)格文件，或者可調(diào)整網(wǎng)格類型，亦或采用其他大變形計算方法（ ALE、CEL、SPH 等）進行控制。

●在彈塑性分析過程中出現(xiàn)不收斂的情況時，應(yīng)首先去掉材料塑性參數(shù)，進行最簡單的線彈性分析。如果計算收斂，則說明材料的塑性參數(shù)有問題，否則說明分析模型中存在其他方面的問題，仔細閱讀報錯信息。

二：集中常用的解決不收斂問題的方法

1、幾何非線性選項解決不收斂問題

在有限元分析中，非線性問題分為三大類：材料非線性、幾何非線性和接觸非線性。當模型結(jié)構(gòu)發(fā)生小變形時，幾何方程也就是應(yīng)變與位移的關(guān)系是線性的，此時不用考慮物體形狀及位置的變化來列平衡方程，很多情況下小變形分析方法滿足精度要求是沒有問題的。但是，當結(jié)構(gòu)發(fā)生大變形問題時，需要考慮變形對平衡的影響，以此滿足精度要求。大變形問題就是幾何非線性問題，因為此時幾何方程中包括位移的二次項。結(jié)構(gòu)發(fā)生幾何非線性可以概括為兩個方面：

●結(jié)構(gòu)發(fā)生大位移小應(yīng)變。當結(jié)構(gòu)發(fā)生大位移小應(yīng)變時我們就可以認為結(jié)構(gòu)屬于幾何非線性結(jié)構(gòu)，此時應(yīng)該在變形后的位形上建立平衡條件，也就是說應(yīng)該考慮變形對平衡的影響，同時幾何方程中應(yīng)包括位移的二次項。如此一來，平衡方程和幾何方程都是非線性方程。

●結(jié)構(gòu)發(fā)生大位移大應(yīng)變，此時屬于幾何和材料雙重非線性。針對橡膠產(chǎn)品的仿真，均屬于此類非線性，此時要引入相應(yīng)的應(yīng)力應(yīng)變關(guān)系，即賦予橡膠網(wǎng)格超彈性屬性。

總的來說，當模型結(jié)構(gòu)經(jīng)受大變形，那么其幾何形狀的變化可能會引起結(jié)構(gòu)的非線性響應(yīng)。位移的大小會影響結(jié)構(gòu)響應(yīng)，若未考慮幾何非線性則難以收斂。分析大變形或大應(yīng)變問題時，在分析步的設(shè)置中打開幾何非線性選項，程序會在分析時考慮大變形或大應(yīng)變對結(jié)果的影響。

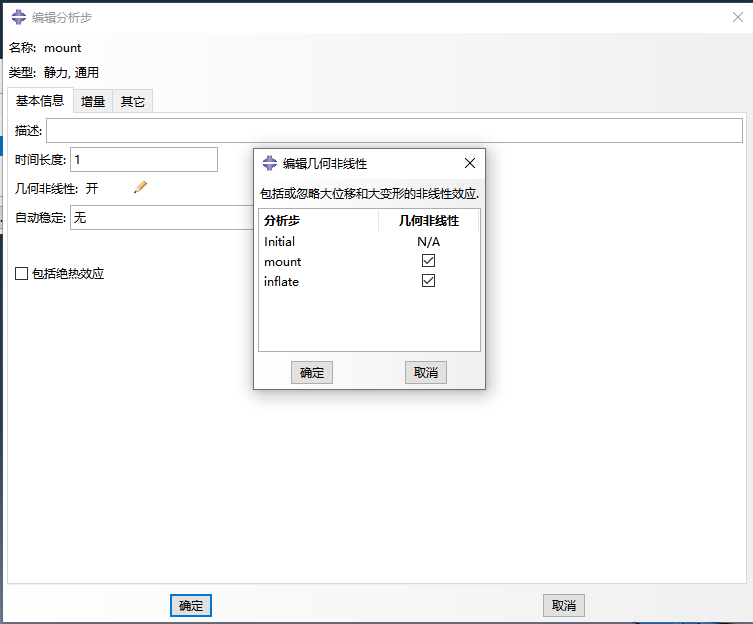
2、合理設(shè)置自動穩(wěn)定解決不收斂問題

除了幾何非線性開關(guān)，在分析步中還可以選擇自動穩(wěn)定功能來解決計算不收斂的問題。自動穩(wěn)定的本質(zhì)是引入粘性規(guī)劃系數(shù)提高收斂性能，使得剛度矩陣中具有接近零或是負的特征值的時候，也能夠計算獲得虛擬解。但是粘性系數(shù)太小、太大都不行：太小不能解決收斂性問題，太大會使得到的解不正確。雖然ABAQUS軟件默認是不考慮自動穩(wěn)定，但是提供了三種方案并內(nèi)置了默認參數(shù)，分析時可根據(jù)具體問題選擇恰當?shù)淖詣臃€(wěn)定條件，解決計算不收斂問題。

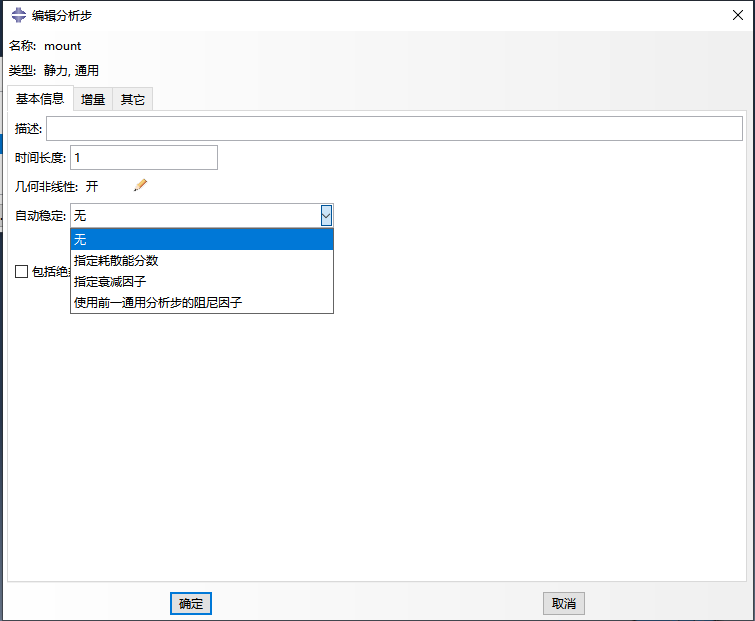
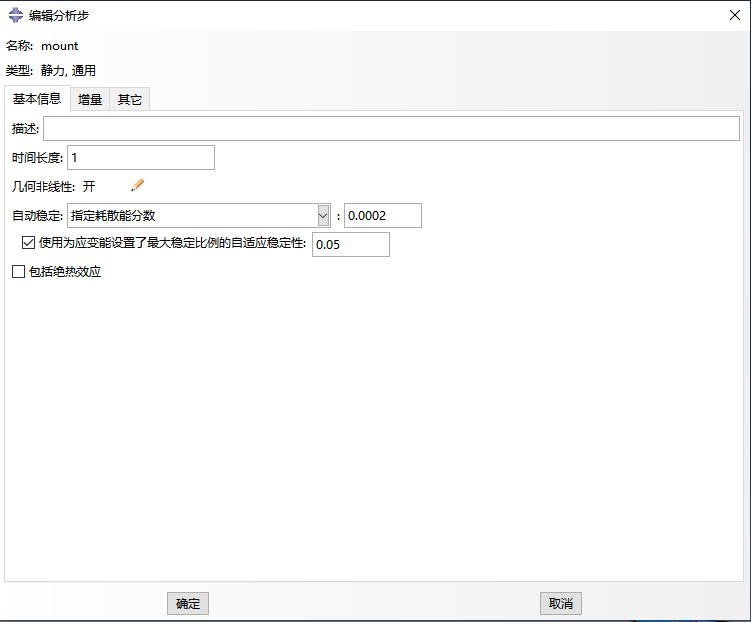
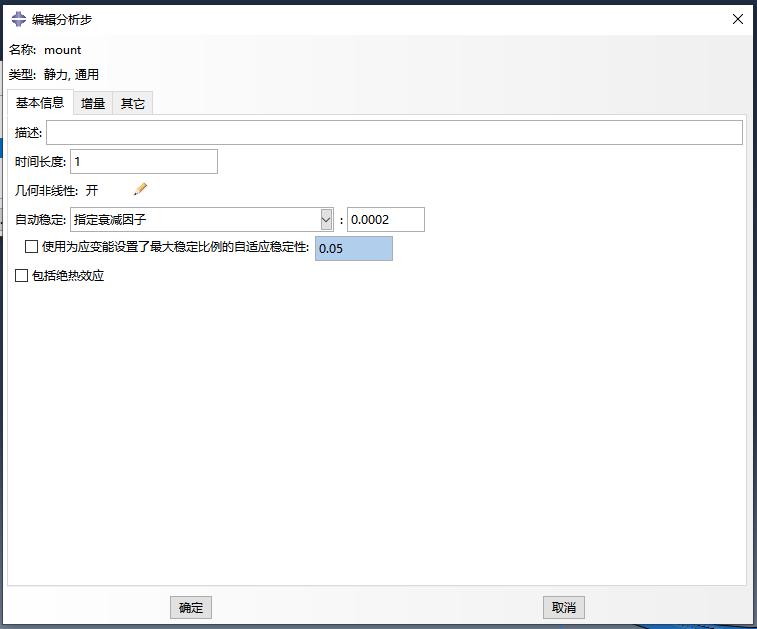
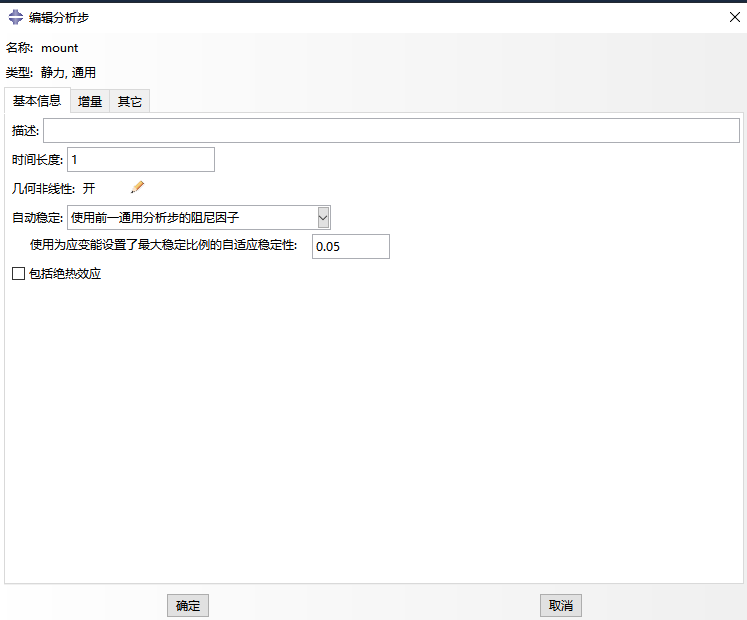
3、劃分網(wǎng)格和選擇單元類型考慮不收斂問題

有限元方法的計算基礎(chǔ)就是網(wǎng)格模型的質(zhì)量。絕大多數(shù)不收斂問題均是由于網(wǎng)格質(zhì)量欠佳導(dǎo)致的，所以在前期劃分網(wǎng)格和選擇單元類型時，要注意以下幾個問題：

●在變形前和變形后，單元的形狀都要保持規(guī)則，不要發(fā)生嚴重扭曲；

●大變形區(qū)域的網(wǎng)格密度要適當，過粗或過細的網(wǎng)格都可能導(dǎo)致收斂問題；

●在彈塑性分析中盡量不要使用二次六面體單元，以免出現(xiàn)體積自鎖現(xiàn)象。建議使用非協(xié)調(diào)單元、一次減縮積分單元和修正的二次四面體單元進行分析。

4、 優(yōu)化接觸屬性解決不收斂問題的思路

在接觸分析中出現(xiàn)不收斂的情況，首先要核對接觸屬性的設(shè)置，確保各接觸面設(shè)置無誤。細化接觸面網(wǎng)格，減小初始增量步，建立確定的接觸關(guān)系。模型中不重要的接觸修改為綁定約束，可以消除剛體位移的同時大大減少了計算時間。

5、調(diào)整通用求解控制屬性解決不收斂問題的思路

對于簡單的非線性問題，一般不需要調(diào)整求解控制參數(shù)，采用軟件默認設(shè)置就能使求解收斂。但對于高度非線性問題難以收斂的情況，可調(diào)整求解控制參數(shù)來滿足收斂條件。例如， Abaqus 默認允許一個增量步內(nèi)最多進行12次迭代，若不能達到穩(wěn)定則判定計算不收斂，此時，可通過迭代次數(shù)，實現(xiàn)該增量步的計算的收斂。

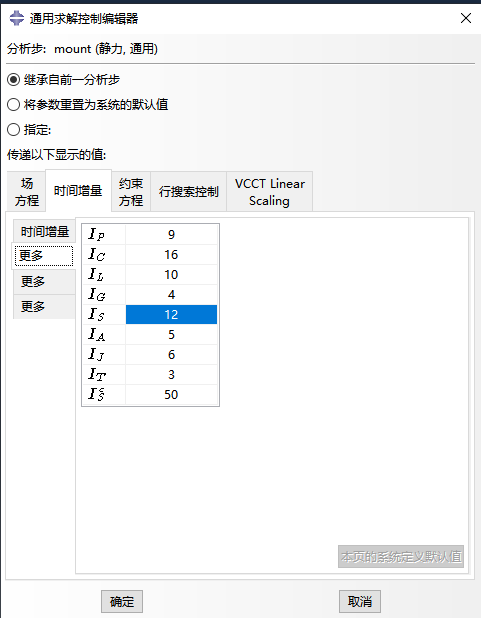
對于可以完成inp文件處理但在初始步出現(xiàn)計算不收斂的情況，檢查其在達到迭代次數(shù)限制以后的時間增量，如果不是很小時，可以通過調(diào)整初始增量步和最小增量步嘗試再次求解。但要注意太小的時間增量意義不大，應(yīng)該從模型當中是否有錯誤去考慮問題。