文 /大眾汽車公司和萊頓大學的 Andrea Skolik
3 月初,Google 與滑鐵盧大學和大眾汽車公司共同發布了 TensorFlow Quantum(TFQ)。TensorFlow Quantum 是一個量子機器學習 (QML) 軟件框架,允許研究員聯合使用 Cirq 和 TensorFlow 的功能。Cirq 和 TFQ 都用于模擬噪聲中等規模量子 (NISQ) 的設備。這些設備當前仍處于實驗階段,因此未經糾錯,還會受到噪聲輸出的影響。
本文介紹的訓練策略可以解決量子神經網絡 (QNN) 中的消失梯度問題,并更好地利用 NISQ 設備提供的資源。
量子神經網絡
訓練 QNN 與訓練經典神經網絡沒有太大不同,區別僅在于優化量子電路的參數而不是優化網絡權重。量子電路的外形如下所示:
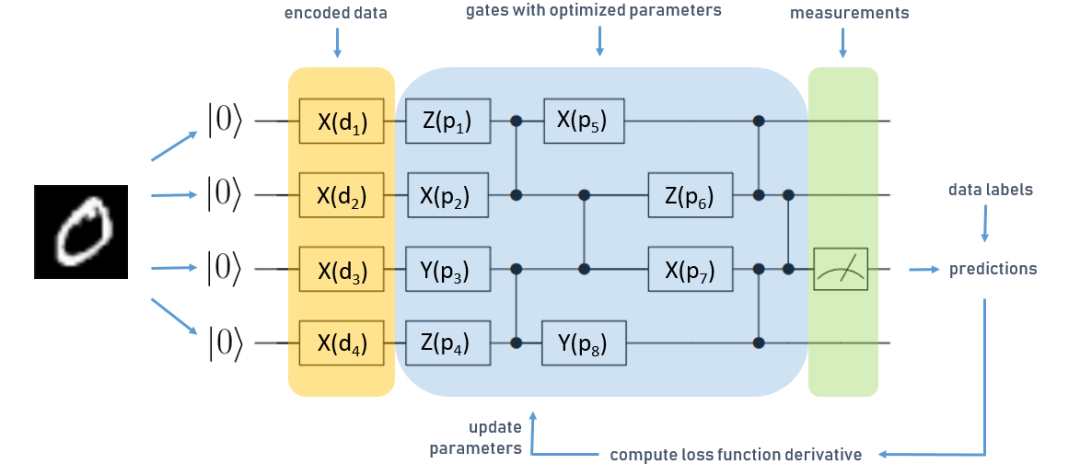
用于四個量子位分類任務的簡化 QNN
電路從左到右讀取,每條水平線對應量子計算機寄存器中的一個量子位,每個量子位都初始化為零狀態。方框表示對按順序執行的量子位的參數化運算(或“門”)。在這種情況下,我們有三種不同類型的運算,X、Y 和 Z。垂直線表示兩個量子邏輯門,可用于在 QNN 中產生糾纏 - 一種使量子計算機勝過經典計算機的資源。我們在每個量子位上將一層表示為一個運算,然后將一系列的門連接成對的量子位,產生糾纏。
上圖為用于學習 MNIST 數字分類的簡化 QNN。
首先,將數據集編碼為量子態。使用數據編碼層來完成這一操作,上圖中標記為橙色。在這種情況下,我們將輸入數據轉換為向量,并將向量值用作數據編碼層運算的參數 d 。基于此輸入執行電路中藍色標記的部分,這一部分代表 QNN 的可訓練門,用 p表示。
量子電路的最后一個運算是測量。計算期間,量子設備對經典位串的疊加執行運算。當我們在電路上執行讀出時,疊加狀態坍縮為一個經典位串,這就是最后的計算輸出。所謂的量子態坍縮是概率性的,要獲得確定性結果,我們需要對多個測量結果取平均值。
上圖中,綠色標記的部分是第三個量子位上的測量,這些測量結果用于預測 MNIST 樣本的標簽。將其與真實數據標簽對比,并像經典神經網絡一樣計算損失函數的梯度。由于參數優化是經典計算機使用 Adam 等優化器處理,因此這些類型的 QNN 稱為“混合量子經典算法”。
消失的梯度,又稱貧瘠高原
事實證明,QNN 與經典神經網絡一樣,也存在消失梯度的問題。由于 QNN 中梯度消失的原因與經典神經網絡有著本質的不同,因此采用了一個新術語:貧瘠高原 (Barren Plateaus)。本文不探討這一重要現象的所有細節,建議感興趣的讀者閱讀首次介紹 QNN 訓練景觀 (Training Landscapes) 中貧瘠高原的文章。
簡而言之,當量子電路被隨機初始化,就會出現貧瘠高原 - 在上述電路中,這意味著隨機選擇運算及其參數。這是訓練參數化量子電路的一個重點問題,并且會隨著量子位數量和電路中層數的增加而越發嚴重,如下圖所示。
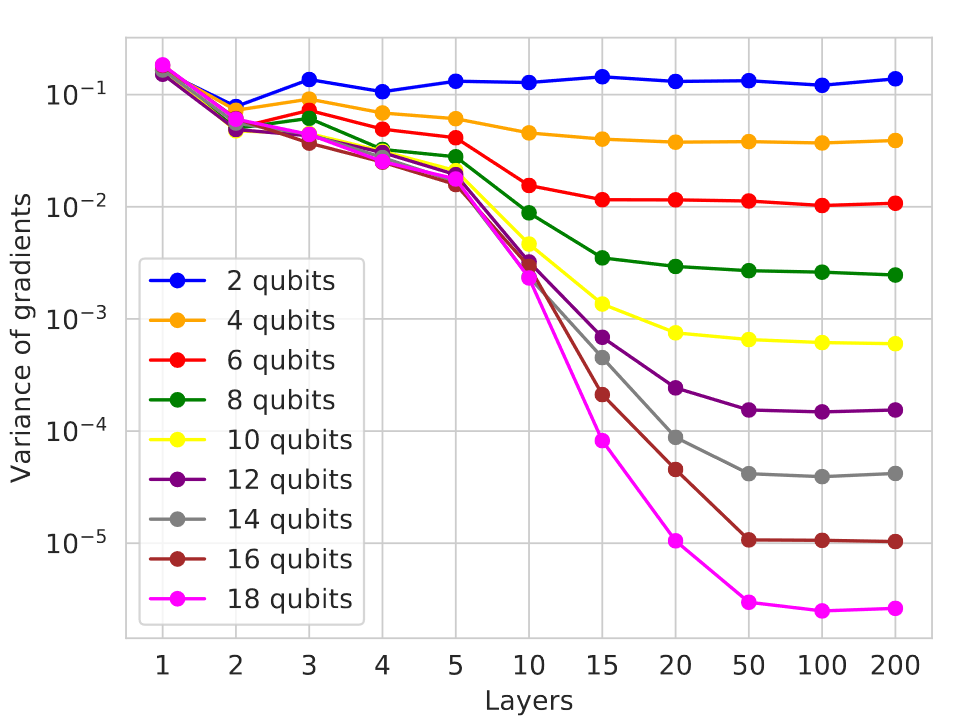
梯度方差根據隨機電路中量子位和層數的變化而衰減
對于下面介紹的算法,關鍵在于電路中添加的層越多,梯度的方差就越小。另一方面,類似于經典神經網絡,QNN 的表示能力也隨著深度的增加而增加。這里的問題是,隨著電路尺寸的增加,優化景觀在很多位置都會趨于平坦,以至于難以找到局部最小值。
注意,對于 QNN,輸出通過多次測量的平均值進行估算。想要估算的量越小,獲得準確結果所需的測量就越多。如果這些量與測量不確定性或硬件噪聲造成的影響相比要小得多,這些量就無法可靠確定,電路優化基本上會變成隨機游走。
為了成功訓練 QNN,必須避免參數的隨機初始化,同時也要阻止 QNN 在訓練過程中由于梯度變小而隨機化,例如在接近局部最小值的時候。為此,我們可以限制 QNN 的架構(例如,通過選擇某些門配置,這需要根據當前任務調整架構),或控制參數的更新,使其不會變得隨機。
分層學習
在我們與 Volkswagen Data:Lab(Andrea Skolik、Patrick van der Smagt、Martin Leib)和 Google AI Quantum(Jarrod R. McClean、Masoud Mohseni)網絡聯合發表的論文 Layerwise learning for quantum neural networks 中,我們介紹了一種避免初始化在高原上并避免網絡在訓練過程中在高原上結束的方法。接下來是一個關于 MNIST 數字二進制分類學習任務的分層學習 (Layerwise Learning) 示例。首先,我們需要定義待堆疊的層的結構。當前的學習任務未經任何假設,因此各層選擇的布局與上圖相同:一層由每個初始化為零的量子位上的隨機門和兩個量子邏輯門組成,兩個量子邏輯門連接量子位以實現糾纏。
我們指定了若干個起始層,在本例中只有一個,將在訓練過程中始終保持活躍狀態,并指定訓練每組層的周期數。另外兩個超參數是每個步驟中添加的新層數,以及一次被最大訓練的層數。在這里選擇一種配置,其中每個步驟中添加兩個層,并凍結除起始層之外的所有先前層的參數,以在每個步驟中僅訓練三個層。將每組層訓練 10 個周期,然后重復此過程十次,直到電路總共由 21 層組成。這里的事實依據是淺層電路會比深層電路產生更大梯度,由此避免了高原上的初始化。
這提供了一個優化過程的良好起點,可以繼續訓練更大的連續層集。對另一個超參數,我們定義了算法第二階段一起訓練的層的百分比。在此將電路分成兩半,交替訓練兩個部分,其中不活動部分的參數始終凍結。一個所有分區都訓練過一次的訓練序列稱為掃描,對這個電路執行掃描,直到損失收斂。當完整參數集始終完成訓練時,我們將這種情況稱為“完全深度學習”(Complete Depth Learning),一個欠佳的更新步驟會影響整個電路并將其引入隨機配置,導致無從逃脫的貧瘠高原。
接下來將我們的訓練策略與訓練 QNN 的標準技術 CDL 進行比較。為了得到公平的結果,我們使用與先前 LL 策略生成的電路架構完全相同的電路架構,但現在在每一步中同時更新所有參數。為了給 CDL 提供訓練的機會,參數將優化為零,而不是隨機優化。由于無法使用真正的量子計算機,因此我們模擬 QNN 的概率輸出,并選擇一個相對較低的值來估計 QNN 每次預測的測量次數——此例中為 10。假設真正的量子計算機上的采樣率為 10kHZ,我們可以估算出訓練運行的實驗性掛鐘時間,如下所示:
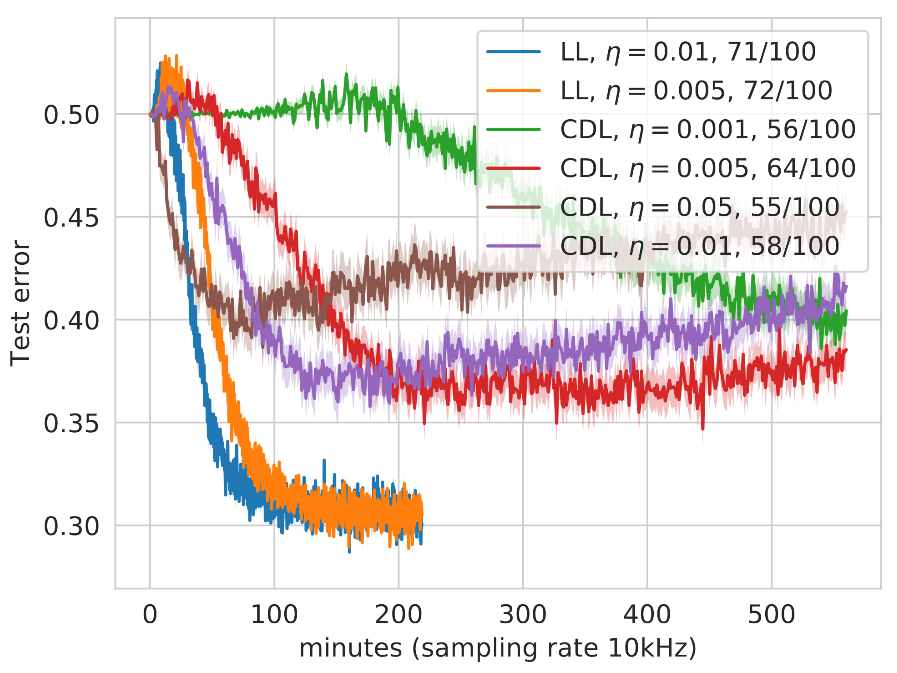
不同學習率 η 的分層深度學習和完全深度學習的比較。每種配置訓練了 100 個電路,并對最終測試誤差低于 0.5(圖例中成功運行的次數)的電路取平均值
通過少量的測量,可以研究 LL 和 CDL 方法不同梯度幅度的影響:如果梯度值較大,則與較小值相比,10 次測量可以提供更多信息。執行參數更新的信息越少,損失的方差就越大,執行錯誤更新的風險也就越大,這將使更新的參數隨機化,并導致 QNN 進入高原。這一方差可以通過更小的學習率降低,因此上圖比較了學習率不同的 LL 和 CDL 策略。
值得注意的是,CDL 運行的測試誤差會隨運行時間的增加而增加,最初看起來像是過擬合。然而,這張圖中的每條曲線都是多次運行的平均值,實際情況是,越來越多的 CDL 運行在訓練過程中隨機化,無法恢復。如圖例所示,與 CDL 相比,LL 運行中有更大一部分在測試集上實現了小于 0.5 的分類誤差,所用時間也更少。
綜上所述,分層學習提高了在更少訓練時間內成功訓練 QNN 的概率,總體上具有更好的泛化誤差,這在 NISQ 設備上尤其實用。
原文標題:介紹量子神經網絡訓練策略,解決消失梯度問題
文章出處:【微信公眾號:TensorFlow】歡迎添加關注!文章轉載請注明出處。
-
量子
+關注
關注
0文章
478瀏覽量
25509 -
量子神經網絡
+關注
關注
0文章
2瀏覽量
1438
原文標題:介紹量子神經網絡訓練策略,解決消失梯度問題
文章出處:【微信號:tensorflowers,微信公眾號:Tensorflowers】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 解決量子神經網絡消失梯度問題 更好利用 NISQ 設備資源
解決量子神經網絡消失梯度問題 更好利用 NISQ 設備資源










評論