1 BN的優點

這里簡單的介紹一下BN，在之前的文章中已經詳細的介紹了BN算法和過程。

BN于2015年由 Google 提出，Google在ICML論文中描述的非常清晰，即在每次SGD時，通過mini-batch來對相應的activation做規范化操作，使得結果（輸出信號各個維度）的均值為0，方差為1。最后的“scale and shift”操作則是為了訓練所需而“刻意”加入的BN能夠有可能還原最初的輸入，從而保證數據中有用信息的留存。

【BN的好處】

BN使得網絡中每層輸入數據的分布相對穩定，加速模型學習速度；

BN使得模型對網絡中的參數不那么敏感，簡化調參過程，使得網絡學習更加穩定；

BN允許網絡使用飽和性激活函數（例如sigmoid，tanh等），緩解梯度消失問題；

BN具有一定的正則化效果。

2 BN的缺點

2.1 受限于Batch size

BN 沿著 batch 維度進行歸一化，其受限于 Batch Size，當 Batch Size 很小時，BN 會得到不準確的統計估計，會導致模型誤差明顯增加

【一般每塊 GPU 上 Batch Size =32 最合適。】

但對于目標檢測，語義分割，視頻場景等，輸入圖像尺寸比較大，而限于GPU顯卡的顯存限制，導致無法設置較大的 Batch Size，如 經典的Faster-RCNN、Mask R-CNN 網絡中，由于圖像的分辨率較大，Batch Size 只能是 1 或 2.

2.2 訓練集與測試集的分布

BN處理訓練集的時候，采用的均值和方差是整個訓練集的計算出來的均值和方差（這一部分沒有看懂的話，可能需要去看一下BN算法的詳解）

所以測試和訓練的數據分布如果存在差異，那么就會導致訓練和測試之間存在不一致現象（Inconsistency）。

3 Group Normalzation

Group Normalization(GN)是由2018年3月份何愷明團隊提出，GN優化了BN在比較小的mini-batch情況下表現不太好的劣勢。

Group Normalization(GN) 則是提出的一種 BN 的替代方法，其是首先將 Channels 劃分為多個 groups，再計算每個 group 內的均值和方法，以進行歸一化。GB的計算與Batch Size無關，因此對于高精度圖片小BatchSize的情況也是非常穩定的，

下圖是比較BN和GN在Batch Size越來越小的變化中，模型錯誤率變化的對比圖：

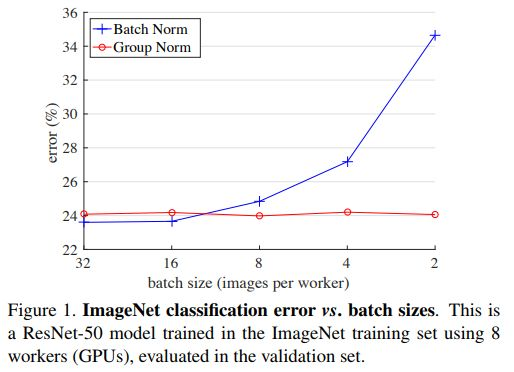
因此在實驗的時候，可以在嘗試使用GN來代替BN哦~

其實不難發現，GN和LN是存在一定的關系的。

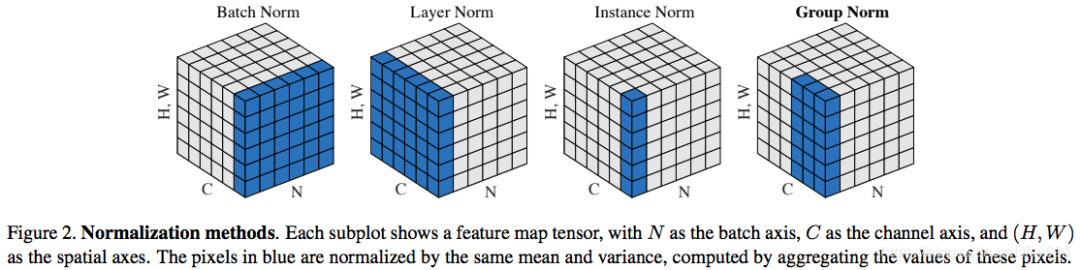
上圖中有四種Normalization的方法。就先從最簡單的Instance Normalization開始分析：

IN：僅僅對每一個圖片的每一個通道最歸一化。也就是說，對【H，W】維度做歸一化。假設一個特征圖有10個通道，那么就會得到10個均值和10個方差；要是一個batch有5個樣本，每個樣本有10個通道，那么IN總共會計算出50個均值方差；

LN：對一個特征圖的所有通道做歸一化。5個10通道的特征圖，LN會給出5個均值方差；

GN：這個是介于LN和IN之間的一種方法。假設Group分成2個，那么10個通道就會被分成5和5兩組。然后5個10通道特征圖會計算出10個均值方差。

BN:這個就是對Batch維度進行計算。所以假設5個100通道的特征圖的話，就會計算出100個均值方差。5個batch中每一個通道就會計算出來一個均值方差。

在GN的論文中，給出了GN推薦的group Number：

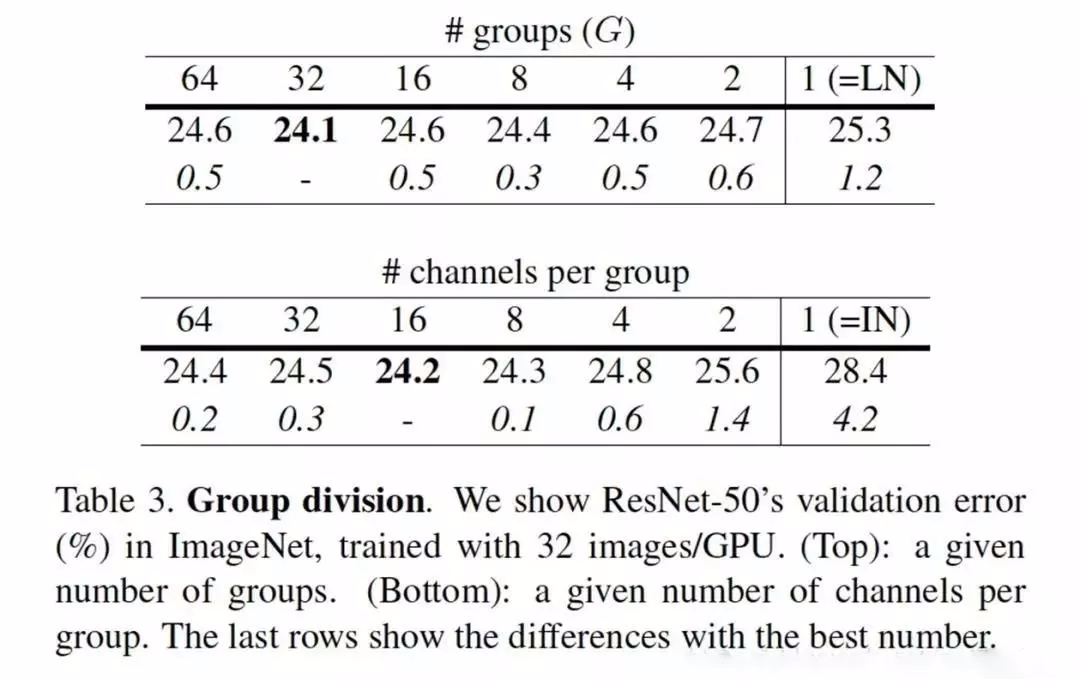
第一個表格展示GN的group Number不斷減小，退化成LN的過程。其實，分組32個group效果最好；

第二個表格展示GN的每一組的channel數目不斷減小，退化成IN的過程。每一組16個channel的效果最好，我個人在項目中也會有優先嘗試16個通道為一組的這種參數設置。

4 PyTorch實現GN

importnumpyasnp importtorch importtorch.nnasnn classGroupNorm(nn.Module): def__init__(self,num_features,num_groups=32,eps=1e-5): super(GroupNorm,self).__init__() self.weight=nn.Parameter(torch.ones(1,num_features,1,1)) self.bias=nn.Parameter(torch.zeros(1,num_features,1,1)) self.num_groups=num_groups self.eps=eps defforward(self,x): N,C,H,W=x.size() G=self.num_groups assertC%G==0 x=x.view(N,G,-1) mean=x.mean(-1,keepdim=True) var=x.var(-1,keepdim=True) x=(x-mean)/(var+self.eps).sqrt() x=x.view(N,C,H,W)

當然，你要是想問PyTorch是否已經集成了GN？那必然的。下面的代碼比較了PyTorch集成的GN和我們手算的GN的結果。

importtorch importtorch.nnasnn x=torch.randn([2,10,3,3])+1 #Torch集成的方法 m=torch.nn.GroupNorm(num_channels=10,num_groups=2) #先計算前面五個通道的均值 firstDimenMean=torch.Tensor.mean(x[0,0:5]) #先計算前面五個通道的方差 firstDimenVar=torch.Tensor.var(x[0,0:5],False) #減去均值乘方差 y2=((x[0][0][0][1]-firstDimenMean)/(torch.pow(firstDimenVar+m.eps,0.5)))*m.weight[0]+m.bias[0] print(y2) y1=m(x) print(m.weight) print(m.bias) print(y1[0,0,0,1])

輸出結果：

tensor(0.4595,grad_fn=) Parametercontaining: tensor([1.,1.,1.,1.,1.,1.,1.,1.,1.,1.],requires_grad=True) Parametercontaining: tensor([0.,0.,0.,0.,0.,0.,0.,0.,0.,0.],requires_grad=True) tensor(0.4595,grad_fn=)