文章由我們熟悉的一維連續(xù)時間信號的卷積逐漸過渡到圖像卷積。文章是循序漸進的,希望想要了解的朋友們可以耐心讀一讀。本人理解有限,如有錯誤還請指出。
(1)先看連續(xù)時間信號的卷積:
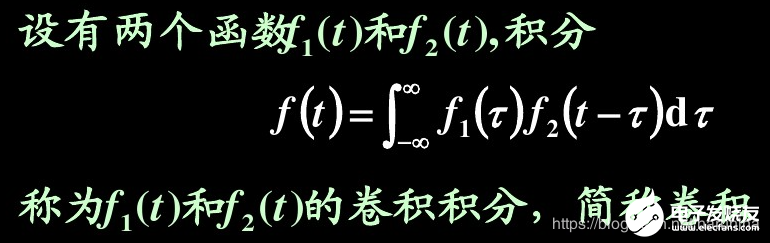
可以看到對與連續(xù)時間信號而言,卷積是一種特殊的積分運算,它的過程就是一個函數(shù)固定不動,另一個函數(shù)先以y軸為對稱軸反轉(zhuǎn),然后不斷執(zhí)行相乘,積分,滑動。
(2.)當我們把連續(xù)時間信號離散化后,卷積的定義便成為了:
其中x(n)和h(n)是參與運算的離散時間信號。在這個定義中,卷積的過程尤為清晰:
在坐標軸上讓x(n)保持不動,先把h(n)反轉(zhuǎn),然后不斷執(zhí)行二者重合部分相乘求和然后讓h(n)滑動的過程。離散時間信號可以看作是一串序列,它是一維的,如果我們把它擴充為二維序列,那不就是圖像了嗎?圖像的本質(zhì)就是灰度值的二維序列。
(3.)下面我們來看什么是圖像的卷積:
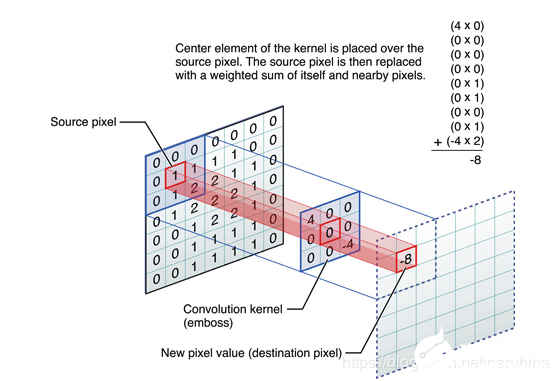
在這幅圖中,source pixel 是我們的圖像,它本質(zhì)是灰度的二維序列,圖中的convolution kernel是什么呢?這個我們稱它為卷積核,這個卷積核就相當于是一維離散信號卷積中的一個參與卷積的信號,圖像本身就相當于是一維離散信號卷積中的另一個離散序列信號,圖像卷積的過程與一維的情況十分類似:圖像卷積就是卷積核在圖像上按行滑動遍歷像素時不斷的相乘求和的過程。舉個例子:如圖中所示,目前卷積核滑動到了圖像左上角,我們把圖像上的9個值與卷積核的9個數(shù)值按照對應位置相乘再相加得到一個和,這個和就是我們得到的卷積值。然后把卷積核向右移動一個像素,再執(zhí)行對應位置相乘再相加的過程得到第二個卷積值,當把所有像素遍歷完成之后我們得到的結(jié)果就構(gòu)成了一幅圖像。這就是卷積得到的圖像。
(4)在圖像處理中,我們不會為了卷積而去卷積,為什么呢?按照卷積的定義,它是與卷積核相乘求和的結(jié)果,如果圖像本身像素的數(shù)據(jù)類型是8位無符號數(shù),那么它的灰度范圍就是0(黑色)到255(白色),這樣以來相乘后的值很容易大于255,那么怎么辦呢?一般就是截斷為255。從我這幾行的描述可以看到,單單卷積確實沒什么用,因為圖像卷積的用武之處不在于此。
(5)圖像卷積常常用于圖像濾波(平滑化),圖像梯度,開運算,閉運算,黑帽運算,頂帽運算等形態(tài)處理,以及基于梯度運算的邊緣提取中。
比如均值濾波的卷積核是這樣的:
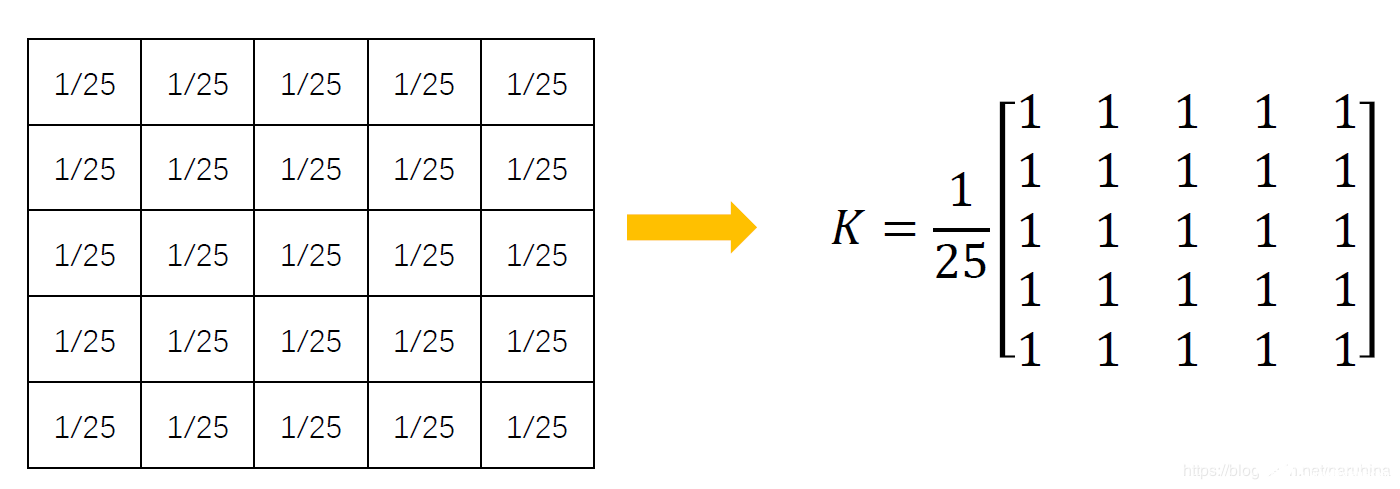
它也是按照卷積運算的過程相乘求和再滑動,只不過它的核里每個值都是1,在求和之后還除以核的大小來取平均。
比如高斯濾波是這樣的:
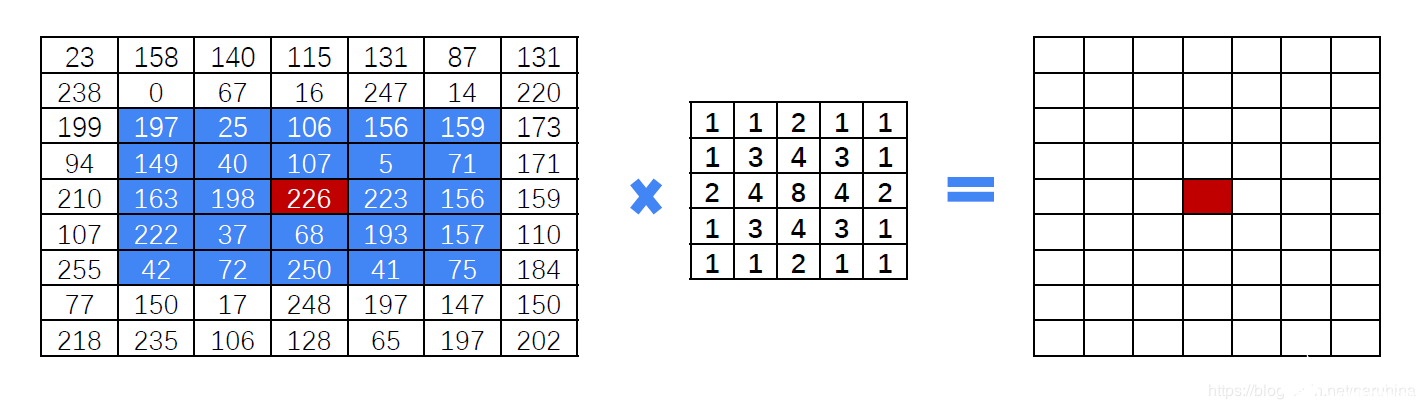
高斯濾波的時候它的核是離中心越近值越大,也就是不同位置的權(quán)重不同。在相乘求和之后會除以核內(nèi)數(shù)值的求和值以保證灰度值不會超出范圍
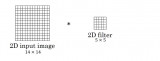
看到這里大家應該會有疑惑,不是正在說卷積嗎,怎么就開始扯濾波了?情況是這樣的:什么是濾波?它的本質(zhì)就是卷積,是按照一定的特殊規(guī)則去卷積,此時使用的卷積核不是隨意的,而是有既定的規(guī)矩的,比如卷積核應取3x3,5x5這樣的具有中心的核,而且核內(nèi)數(shù)值的分布也是有規(guī)定的,視不同的濾波方式而定。
講了這么多我還沒有說什么是卷積核,卷積核就是一種求和的規(guī)則,是一種映射的規(guī)則。原圖像像素點的值與對應位置上的卷積核的值相乘然后按權(quán)重相加處理,這個過程用數(shù)學去表示不就是src(原圖像) x kernel(映射規(guī)則)=result(卷積的結(jié)果) 嗎?所以卷積核就是一種運算的規(guī)則,由卷積核規(guī)則的不同衍生出了不同的濾波方式,不同的梯度運算方式等。
講到這里我還想再說一說濾波,為什么卷積一下就濾波了呢?我舉個例子:就比如上文寫到的均值濾波,它的映射規(guī)則(就是卷積核)不就是全部都是1除以核大小嗎?也就是說原圖像與這樣的卷積核卷積的結(jié)果就是原圖像的像素值乘以卷積核對應位置的值相加,很巧合的是核內(nèi)的值都是1/25(這是對于5x5大小的核來說的),那這樣看很顯然,卷積的結(jié)果就是把原圖像像素值相加取平均值。這樣一來像素與像素之間的差異性就變小了,圖像中分明的線條和邊界就是像素值迥然的差異所導致的,差異性減小導致邊界就模糊了,圖像自然就變得平滑了。說到這里還是沒說濾波這個概念,我們在數(shù)字信號處理中接觸的諸如高通濾波就是為了濾除高頻信號(分布在π附近的信號),在圖像濾波中也是如此。我剛才說濾波后像素與像素之間的差異性減小了,這不就意味著濾除了高頻成分嗎?高頻信號的定義就是變化很快的信號,在圖像中,如果兩個像素差異很大就意味著移動一個像素的距離帶來的變化就是巨大的,而當這巨大的變化連接起來就是圖像中的圖形的邊界或線條,這樣就是為什么線條被稱之為高頻信號。
我想看到這里大家應該就理解了為什么卷積一下就能濾波了吧,卷積的一種應用形式就是濾波,當然不同的卷積核有不同的卷積效果,所以卷積還有諸如梯度運算等其他的應用形式,差別就在于卷積核的不同
總結(jié)起來就是:圖像卷積靠卷積核完成,卷積核規(guī)定了運算的規(guī)則,濾波是卷積運算所帶來的效果。不同的卷積核所得到的卷積效果不同,故衍生出了不同種類的濾波,形態(tài)運算,梯度運算等等概念。由此可見:卷積是圖像處理的基礎(chǔ),許許多多處理方式都是離不開卷積的
-
濾波
+關(guān)注
關(guān)注
10文章
667瀏覽量
56670 -
圖像處理
+關(guān)注
關(guān)注
27文章
1293瀏覽量
56781 -
高斯濾波
+關(guān)注
關(guān)注
0文章
18瀏覽量
8072 -
卷積
+關(guān)注
關(guān)注
0文章
95瀏覽量
18526
發(fā)布評論請先 登錄
相關(guān)推薦
FFT與DFT計算時間的比較及圓周卷積代替線性卷積的有效性實
關(guān)于對信號的反卷積問題
CNN之卷積層
卷積神經(jīng)網(wǎng)絡一維卷積的處理過程
簡談卷積—幽默笑話談卷積
實驗一 連續(xù)時間系統(tǒng)卷積的數(shù)值計算
一種輕量級時間卷積網(wǎng)絡設(shè)計方案





 淺談一維連續(xù)時間信號的卷積逐漸過渡到圖像卷積
淺談一維連續(xù)時間信號的卷積逐漸過渡到圖像卷積

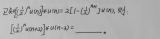










評論