摘要： 深度學習背后的主要原因是人工智能應該從人腦中汲取靈感。本文就用一個小例子無死角的介紹一下深度學習！

人腦模擬

深度學習背后的主要原因是人工智能應該從人腦中汲取靈感。此觀點引出了“神經網絡”這一術語。人腦中包含數十億個神經元，它們之間有數萬個連接。很多情況下，深度學習算法和人腦相似，因為人腦和深度學習模型都擁有大量的編譯單元（神經元），這些編譯單元（神經元）在獨立的情況下都不太智能，但是當他們相互作用時就會變得智能。

我認為人們需要了解到深度學習正在使得很多幕后的事物變得更好。深度學習已經應用于谷歌搜索和圖像搜索，你可以通過它搜索像“擁抱”這樣的詞語以獲得相應的圖像。－杰弗里·辛頓

神經元

神經網絡的基本構建模塊是人工神經元，它模仿了人類大腦的神經元。這些神經元是簡單、強大的計算單元，擁有加權輸入信號并且使用激活函數產生輸出信號。這些神經元分布在神經網絡的幾個層中。

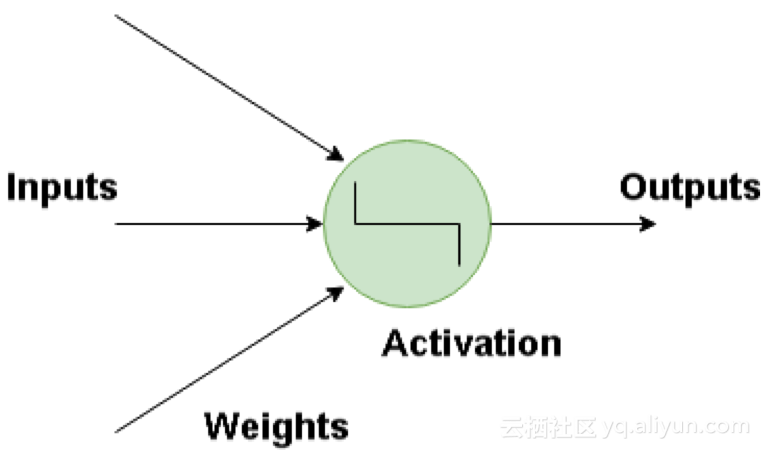
inputs 輸入 outputs 輸出 weights 權值 activation 激活

人工神經網絡的工作原理是什么？

深度學習由人工神經網絡構成，該網絡模擬了人腦中類似的網絡。當數據穿過這個人工網絡時，每一層都會處理這個數據的一方面，過濾掉異常值，辨認出熟悉的實體，并產生最終輸出。

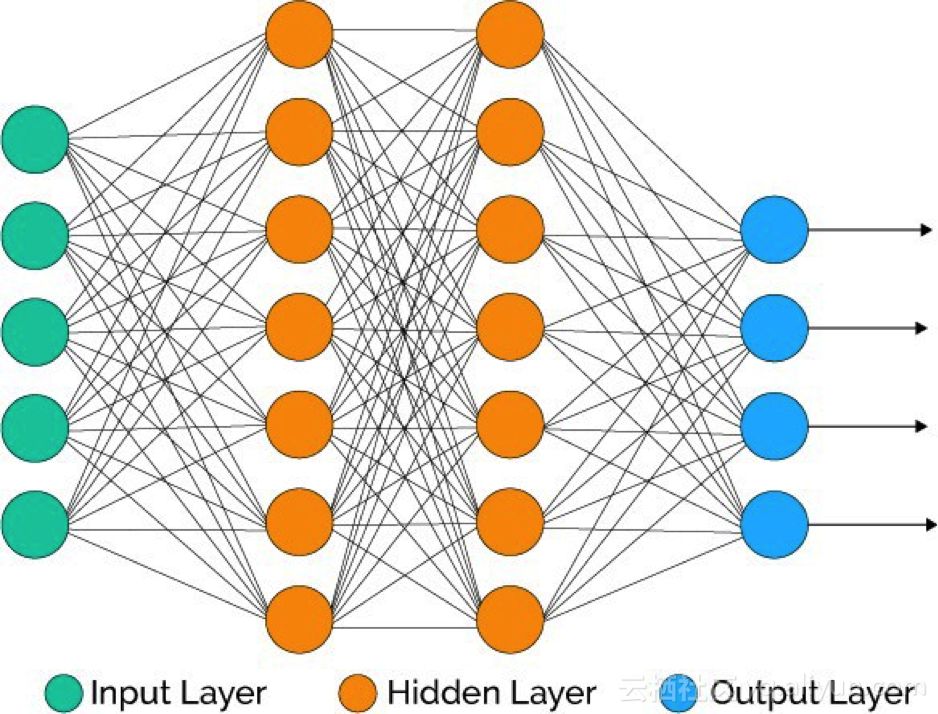
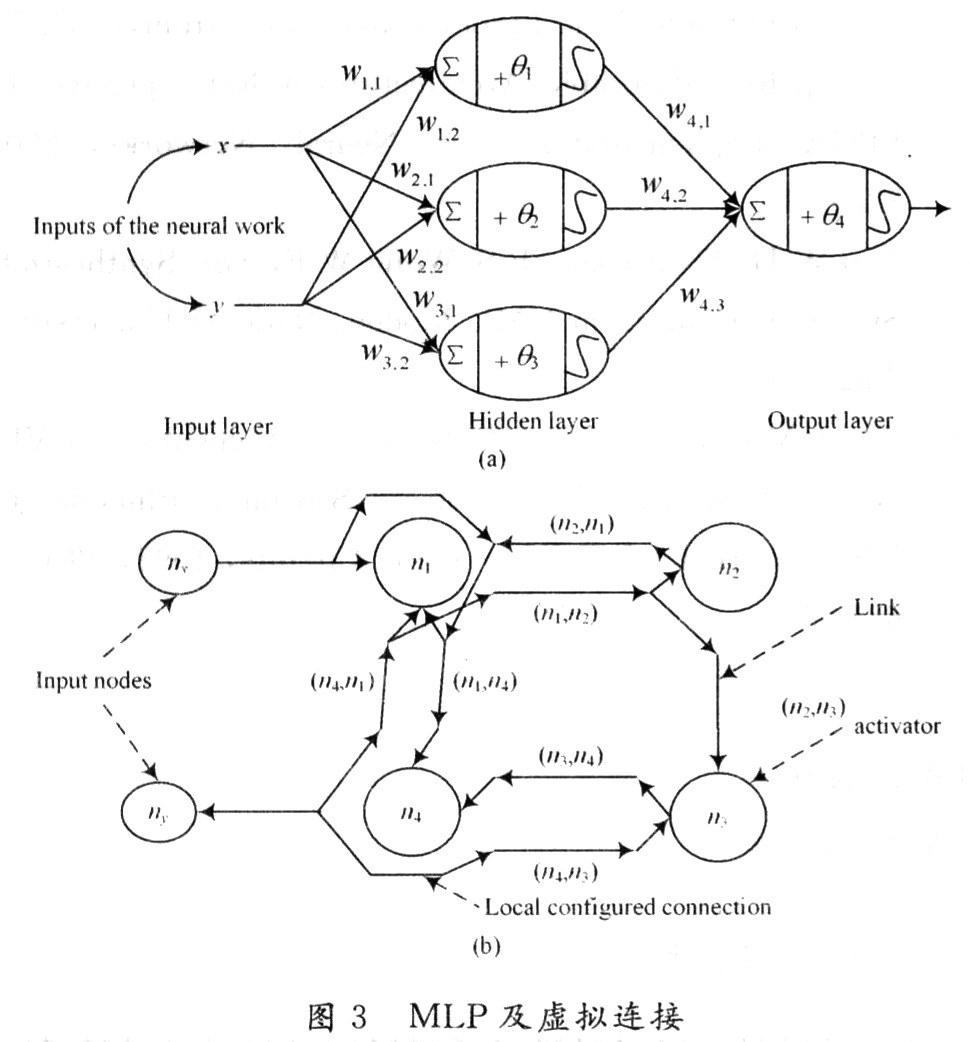
輸入層：該層由神經元組成，這些神經元只接收輸入信息并將它傳遞到其他層。輸入層的圖層數應等于數據集里的屬性或要素的數量。輸出層：輸出層具有預測性，其主要取決于你所構建的模型類型。隱含層：隱含層處于輸入層和輸出層之間，以模型類型為基礎。隱含層包含大量的神經元。處于隱含層的神經元會先轉化輸入信息，再將它們傳遞出去。隨著網絡受訓練，權重得到更新，從而使其更具前瞻性。

神經元的權重

權重是指兩個神經元之間的連接的強度或幅度。你如果熟悉線性回歸的話，可以將輸入的權重類比為我們在回歸方程中用的系數。權重通常被初始化為小的隨機數值，比如數值0-1。

前饋深度網絡

前饋監督神經網絡曾是第一個也是最成功的學習算法。該網絡也可被稱為深度網絡、多層感知機（MLP）或簡單神經網絡，并且闡明了具有單一隱含層的原始架構。每個神經元通過某個權重和另一個神經元相關聯。

該網絡處理向前處理輸入信息，激活神經元，最終產生輸出值。在此網絡中，這稱為前向傳遞。

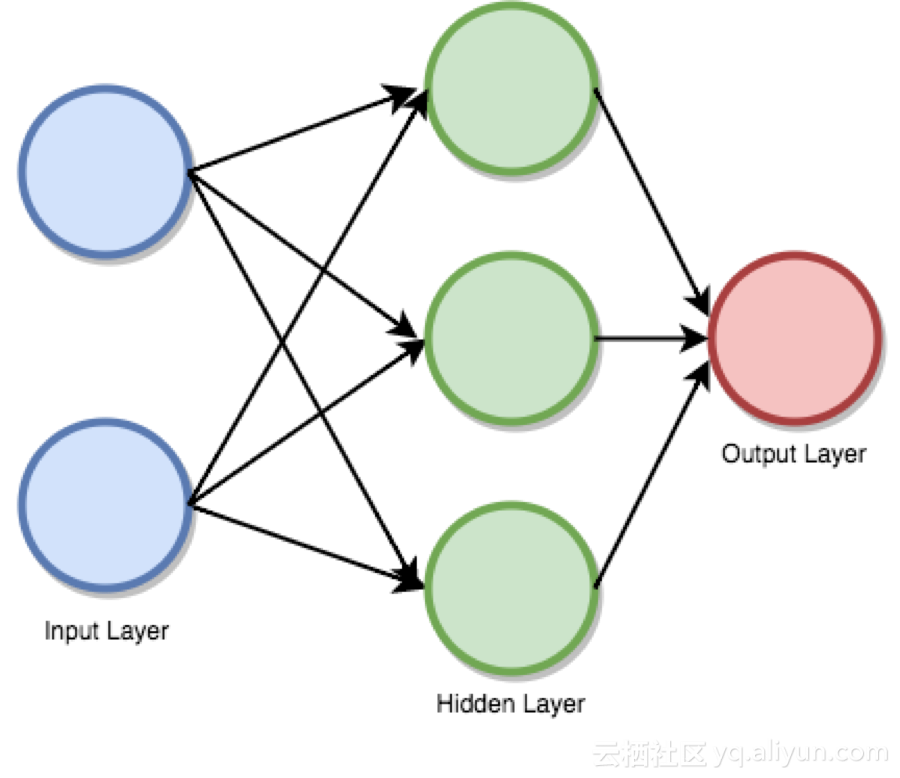
input layer 輸入層 hidden layer 輸出層 output layer 輸出層

激活函數

激活函數就是求和加權的輸入到神經元的輸出的映射。之所以稱之為激活函數或傳遞函數是因為它控制著激活神經元的初始值和輸出信號的強度。

用數學表示為：

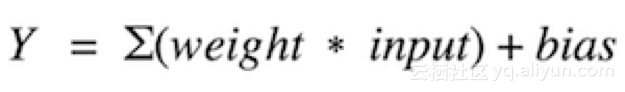
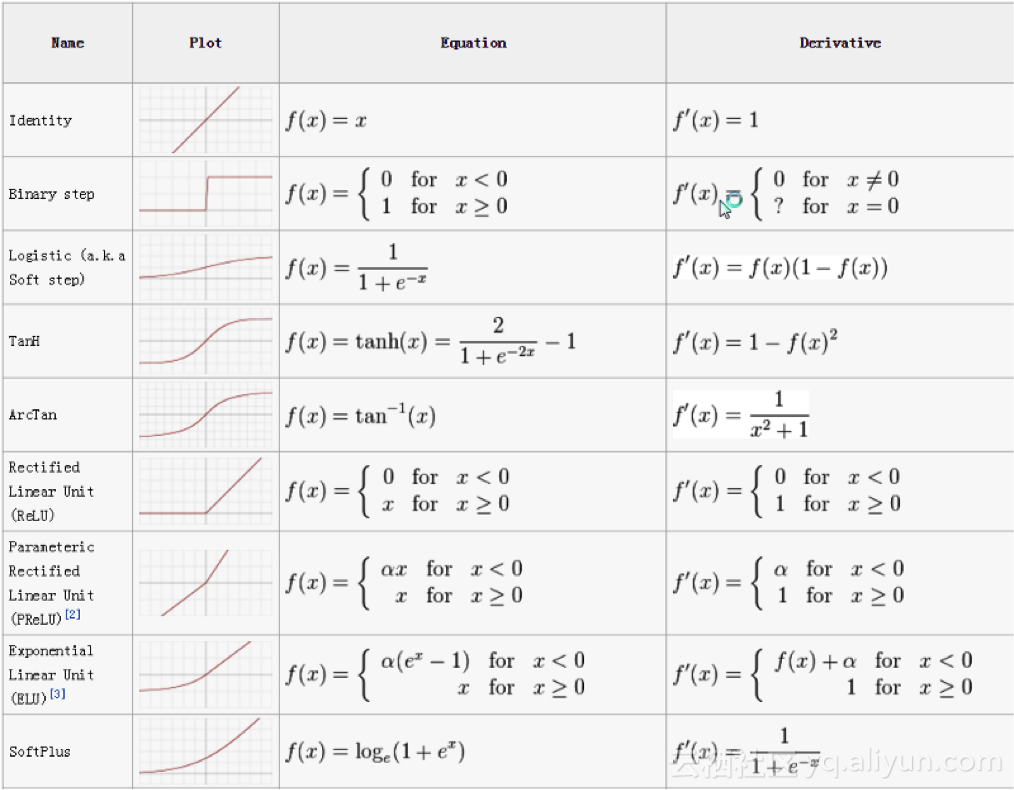
我們有許多激活函數，其中使用最多的是整流線性單元函數、雙曲正切函數和solfPlus函數。

激活函數的速查表如下：

反向傳播

在網絡中，我們將預測值與預期輸出值相比較，并使用函數計算其誤差。然后，這個誤差會傳回這個網絡，每次傳回一個層，權重也會根絕其導致的誤差值進行更新。這個聰明的數學法是反向傳播算法。這個步驟會在訓練數據的所有樣本中反復進行，整個訓練數據集的網絡更新一輪稱為一個時期。一個網絡可受訓練數十、數百或數千個時期。

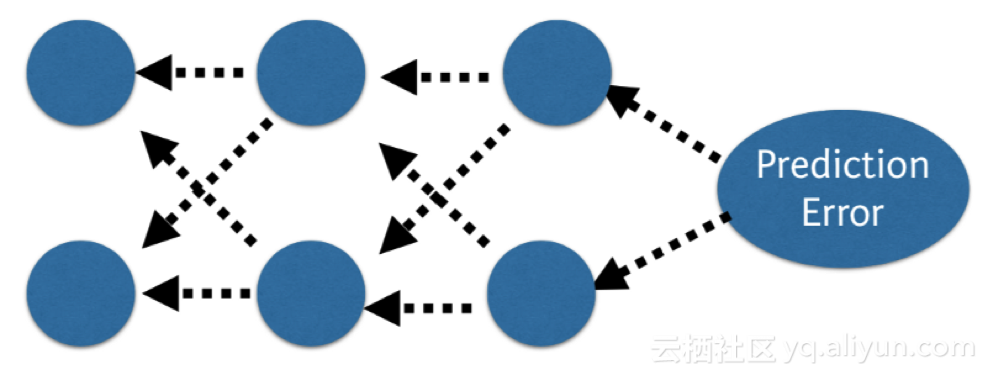
prediction error 預測誤差

代價函數和梯度下降

代價函數度量了神經網絡對給定的訓練輸入和預期輸出“有多好”。該函數可能取決于權重、偏差等屬性。

代價函數是單值的，并不是一個向量，因為它從整體上評估神經網絡的性能。在運用梯度下降最優算法時，權重在每個時期后都會得到增量式地更新。

兼容代價函數

用數學表述為差值平方和：

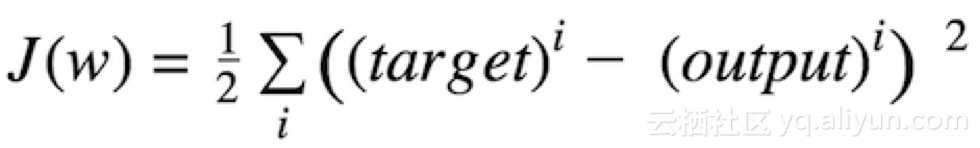
target 目標值 output 輸出值

權重更新的大小和方向是由在代價梯度的反向上采取步驟計算出的。

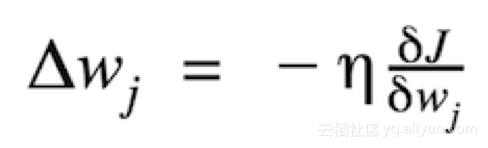
其中η 是學習率

其中Δw是包含每個權重系數w的權重更新的向量，其計算方式如下：

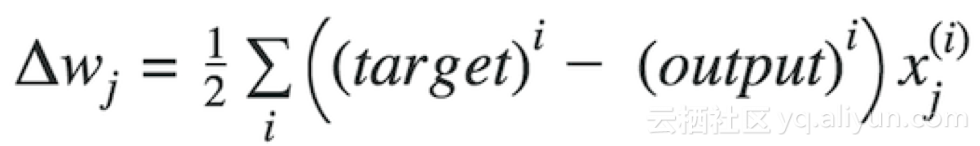
target 目標值 output 輸出值

圖表中會考慮到單系數的代價函數

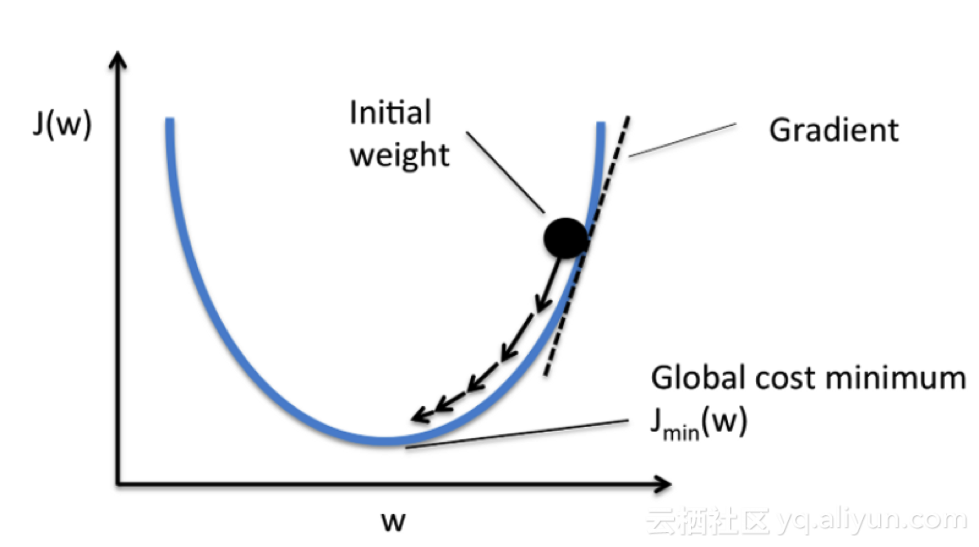
initial weight 初始權重 gradient 梯度 global cost minimum 代價極小值

在導數達到最小誤差值之前，我們會一直計算梯度下降，并且每個步驟都會取決于斜率（梯度）的陡度。

多層感知器（前向傳播）

這類網絡由多層神經元組成，通常這些神經元以前饋方式（向前傳播）相互連接。一層中的每個神經元可以直接連接后續層的神經元。在許多應用中，這些網絡的單元會采用S型函數或整流線性單元（整流線性激活）函數作為激活函數。

現在想想看要找出處理次數這個問題，給定的賬戶和家庭成員作為輸入

要解決這個問題，首先，我們需要先創建一個前向傳播神經網絡。我們的輸入層將是家庭成員和賬戶的數量，隱含層數為1， 輸出層將是處理次數。

將圖中輸入層到輸出層的給定權重作為輸入：家庭成員數為2、賬戶數為3。

現在將通過以下步驟使用前向傳播來計算隱含層（i，j）和輸出層（k）的值。

步驟：
1， 乘法－添加方法。
2， 點積（輸入＊權重）。
3，一次一個數據點的前向傳播。
4， 輸出是該數據點的預測。

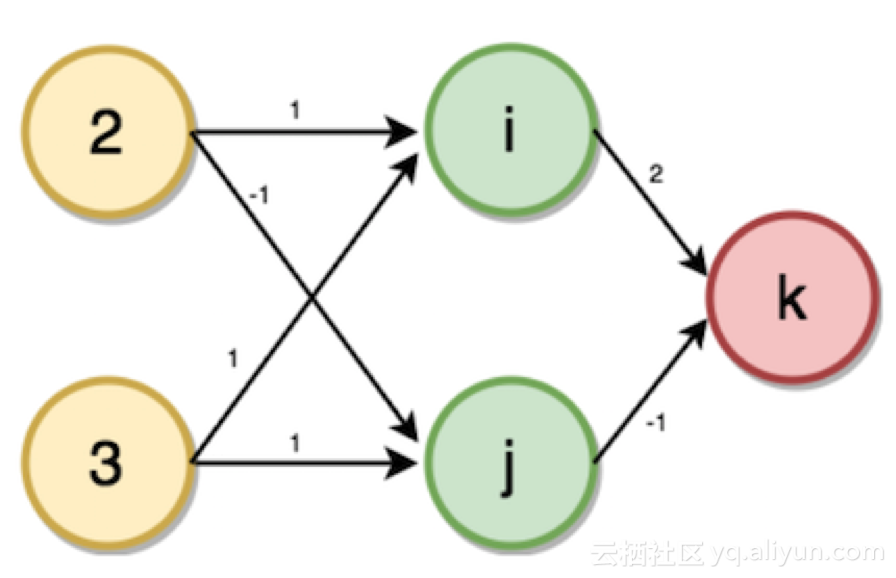
i的值將從相連接的神經元所對應的輸入值和權重中計算出來。

i = (2 * 1) + (3 * 1) → i = 5

同樣地，j = (2 * -1) + (3 * 1) → j = 1

K = (5 * 2) + (1 * -1) → k = 9

Python中的多層感知器問題的解決

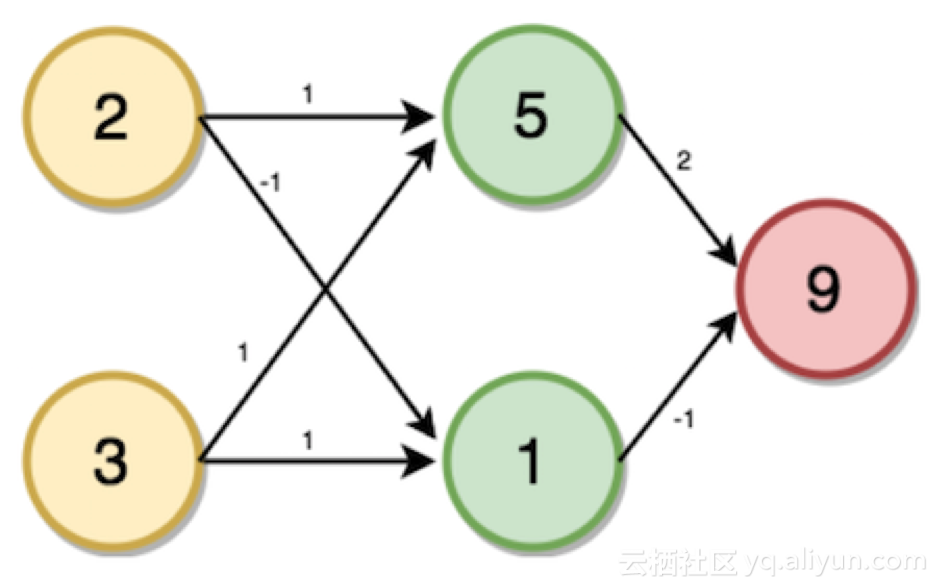
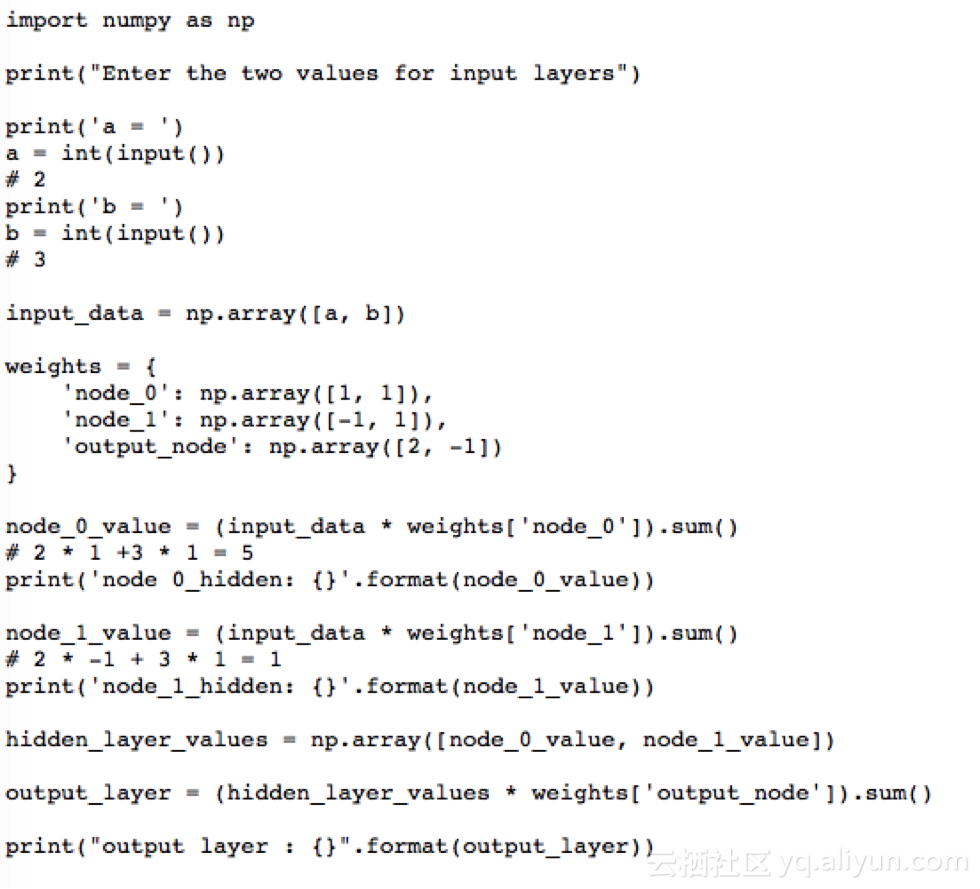
激活函數的使用

為了使神經網絡達到其最大預測能力，我們需要在隱含層應用一個激活函數，以捕捉非線性。我們通過將值代入方程式的方式來在輸入層和輸出層應用激活函數。

這里我們使用整流線性激活（ReLU）:

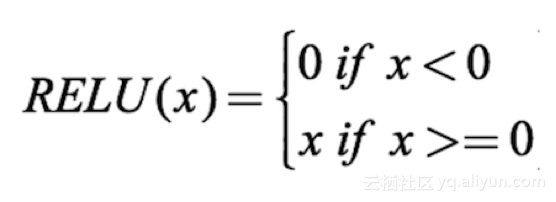
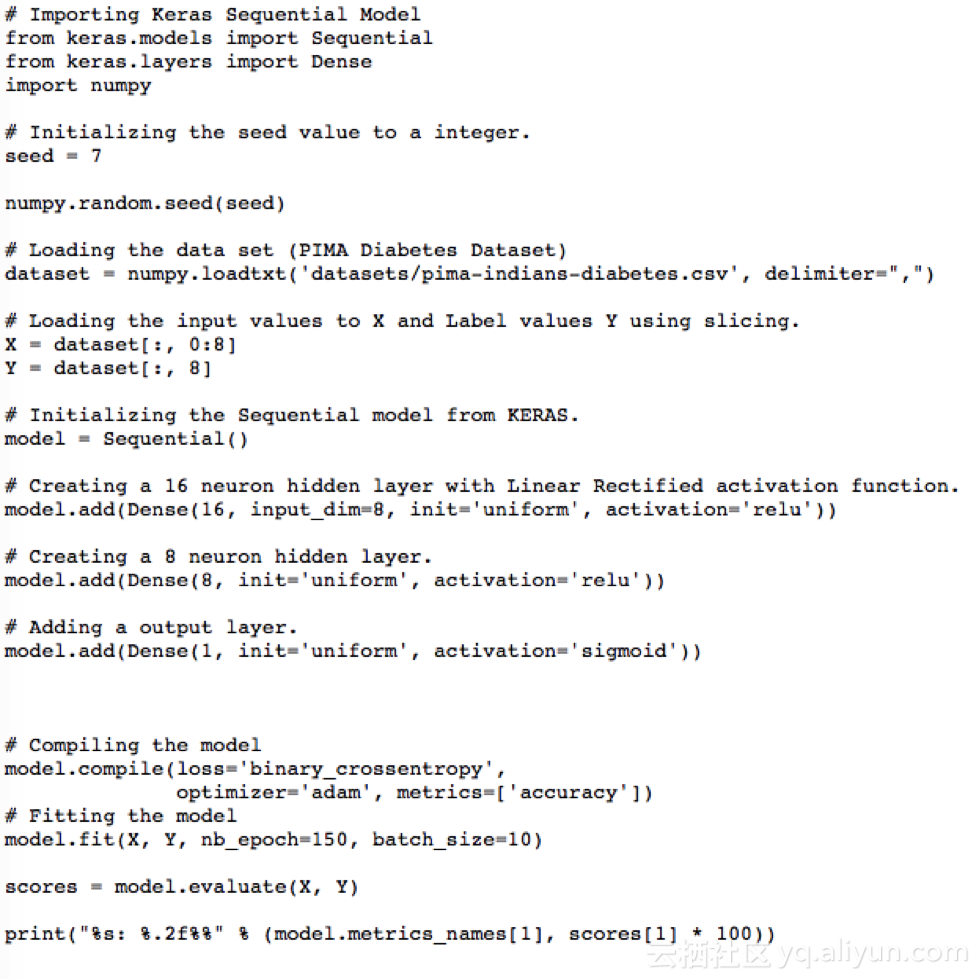
用Keras開發第一個神經網絡

關于Keras：

Keras是一個高級神經網絡的應用程序編程接口，由Python編寫，能夠搭建在TensorFlow,CNTK,或Theano上。

使用PIP在設備上安裝Keras,并且運行下列指令。

在keras執行深度學習程序的步驟
1，加載數據；
2，創建模型；
3，編譯模型；
4，擬合模型；
5，評估模型；

開發Keras模型

全連接層用Dense表示。我們可以指定層中神經元的數量作為第一參數，指定初始化方法為第二參數，即初始化參數，并且用激活參數確定激活函數。既然模型已經創建，我們就可以編譯它。我們在底層庫（也稱為后端）用高效數字庫編譯模型，底層庫可以用Theano或TensorFlow。目前為止，我們已經完成了創建模型和編譯模型，為進行有效計算做好了準備。現在可以在PIMA數據上運行模型了。我們可以在模型上調用擬合函數f（），以在數據上訓練或擬合模型。

我們先從KERAS中的程序開始，

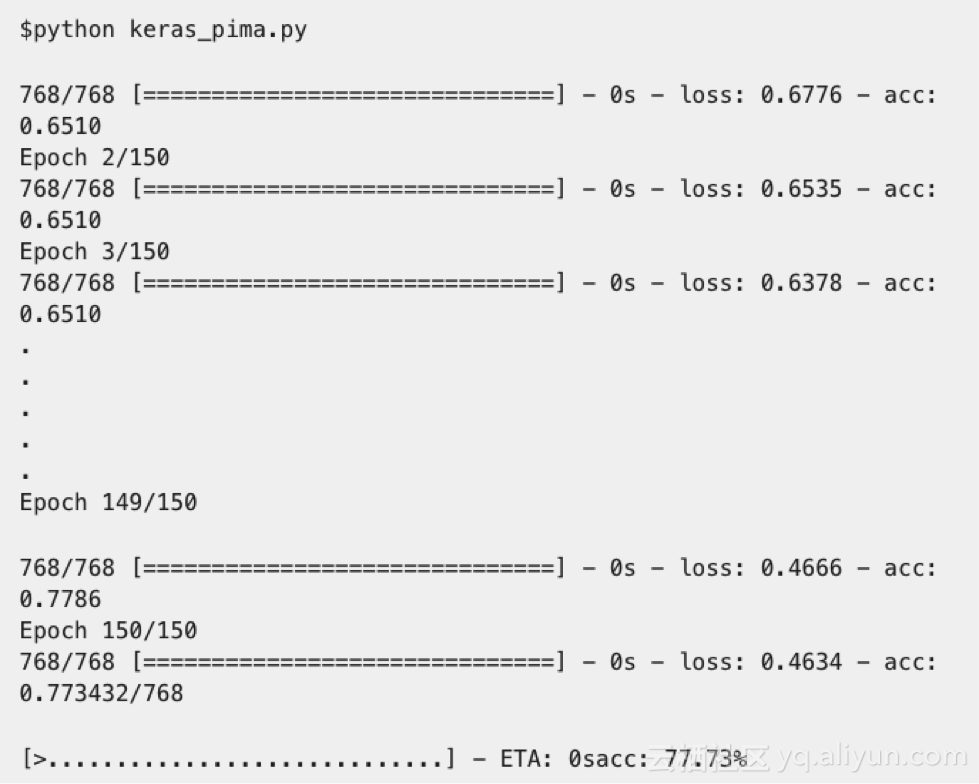
神經網絡一直訓練到150個時期，并返回精確值。

本文由北郵@愛可可-愛生活老師推薦，阿里云云棲社區組織翻譯。

作者：Vihar Kurama

譯者：荷葉。