本文通過案例介紹了正態分布和貝塔分布的概念。
正態分布
正態分布,是一種非常常見的連續概率分布,其也叫做常態分布(normal distribution),或者根據其前期的研究貢獻者之一高斯的名字來稱呼,高斯分布(Gaussian distribution)。正態分布是自然科學與行為科學中的定量現象的一個方便模型。
各種各樣的心理學測試結果和物理現象的觀測值,比如光子計數等都被發現近似地服從正態分布。甚至生活中很多現象的表征結果也符合正態分布的分布規律。盡管這些現象的根本原因經常是未知的,甚至被采樣的樣本的原始群體分布并不服從正態分布,但這個變量的采樣分布均值仍會近似服從正態分布。
正態分布的概率密度函數呈左右對稱的鐘形,其具體表達式為:
![]()
因為正態分布是如此的常見而這個式子是如此的奇怪,我們打算重溫高斯當年的推導過程,但部分細節不會那么嚴謹的證明,只是帶領大家看看高斯當年的思路是如何的。
首先,高斯事先假定了如下條件,才得到了正態分布的連續密度函數。
即: 誤差分布導出的極大似然估計 = 算術平均值
這里我們把全部過程用直白的語言復述一遍。


貝塔分布
貝塔分布,beta分布,簡單來說,就是一個事件出現的概率的概率密度分布。
舉個例子,籃球比賽的三分命中率是衡量籃球后衛運動員很重要的一個指標。通過過去的歷史經驗,我們知道運動員的三分命中率很難超過40%。假如老張是一個優秀老練的籃球后衛,其過去歷史的三分命中率是35%,總投數為10000次,命中次為3500次。請問他在新賽季剛開始的時候,得到了一次三分投球機會,請問他這次投中的概率服從什么分布呢?
我們必須清楚,這個概率一定不是確定的,而是服從某種分布。這個概率密度分布函數應該在0.35處最大,沿兩邊逐漸遞減。
這個概率就服從beta分布。確切的說,是服從
還有個運動員小張,而小張很年輕也很優秀,他的歷史三分命中率也是35%,但是總投數為1000次,命中次數為350次。請問他在新賽季首投三分,命中概率的分布和老張一樣嗎?
明顯不一樣!雖然他們的歷史投球命中率都是35%,但是我們直覺認為老張比小張更靠譜,老張首投命中的概率密度分布應該在0.35附近高于小張的。事實上,我們可以迅速借助python的scipy庫中內置的beta統計方法。

我們來看一下圖像。

的確如此。那么beta分布的具體表達式是什么呢?

關于伽馬函數和貝塔函數,這里我們不做贅述。
需要指出的是,看起來beta分布的概率密度函數和高斯分布的曲線很像,實則不然。
再舉個例子,假如老張的孫子也想做做運動員,老張煞有介事的統計了小小張的歷史三分投數,為5投1中。問他下一次投球,也就是第六次投球,命中的概率的分布是怎樣的?如果過去是5投2中,5投3中,和5投4中呢?

可以看到,beta分布的PDF和高斯分布的曲線形狀差別可大了。
編輯:hfy
-
函數
+關注
關注
3文章
4331瀏覽量
62595 -
高斯分布
+關注
關注
0文章
6瀏覽量
2750
發布評論請先 登錄
相關推薦
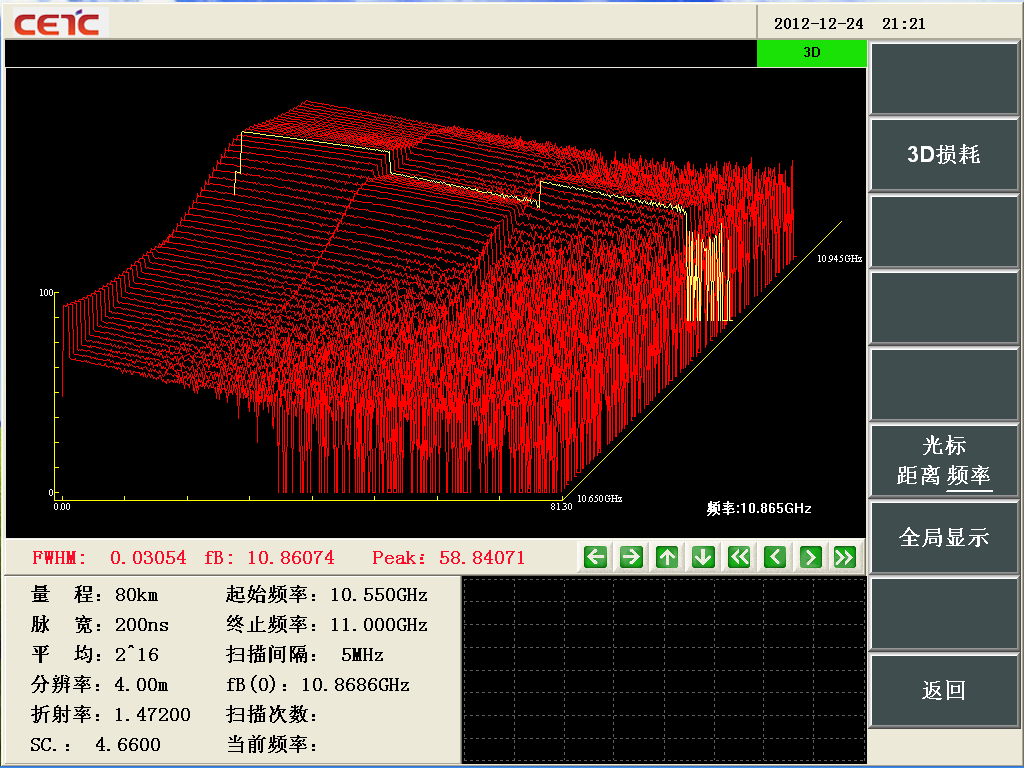
6419,6419A光纖應變分布測試儀
圖像高斯濾波的原理及FPGA實現思路

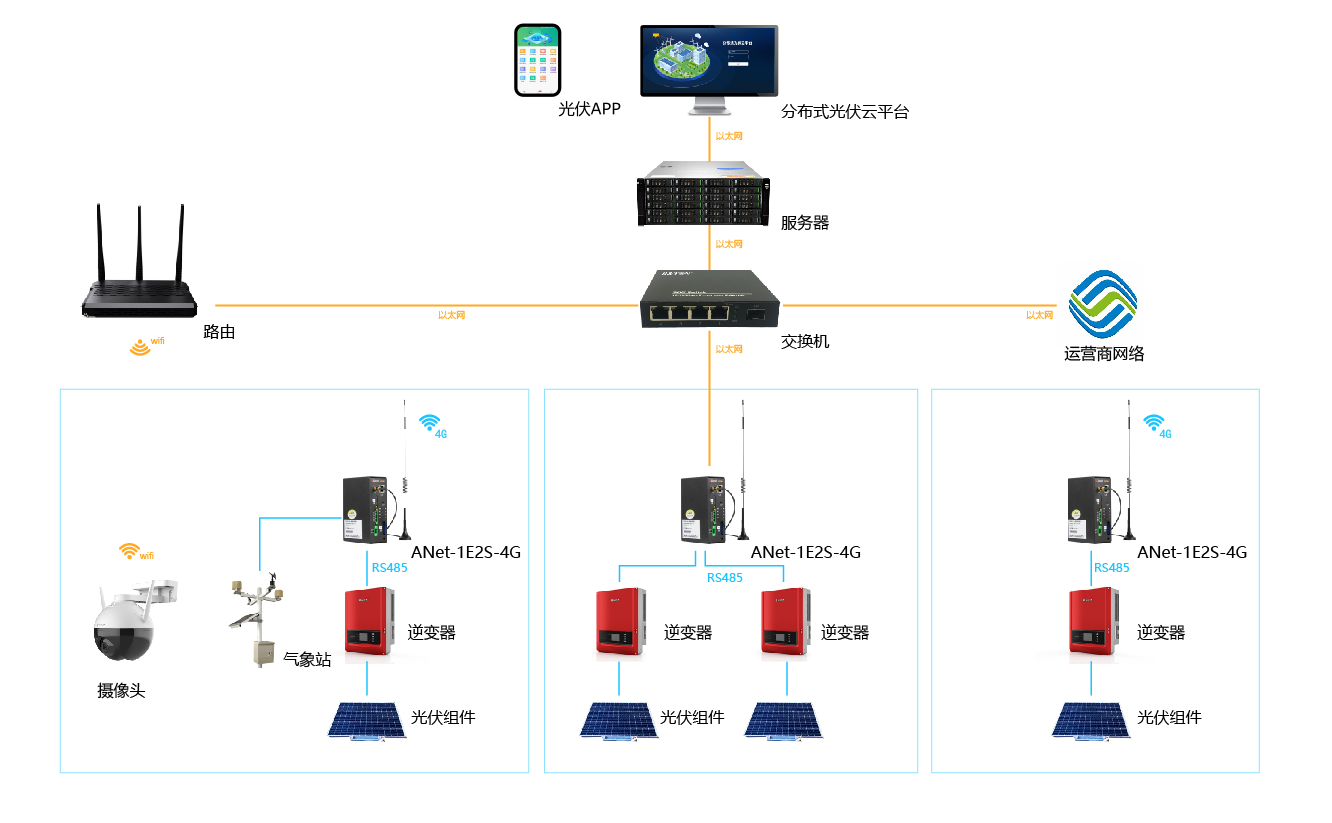
分布式光伏為企業帶來哪些便捷!
分布式通信的原理和實現高效分布式通信背后的技術NVLink的演進
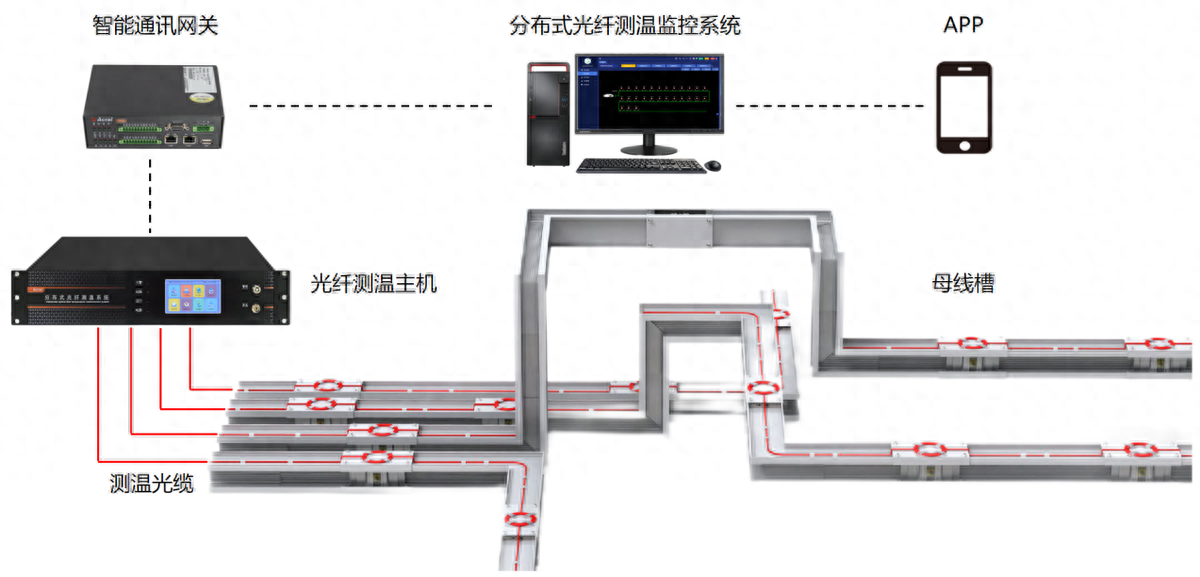
分布式光纖測溫是什么?應用領域是?
雨刮器壓力分布檢測wipe有用嗎?
安科瑞分布式光伏系統在某重工企業18MW分布式光伏中應用
分布式SCADA系統的特點的組成
導體靜電平衡狀態的基本特征和電荷分布
Redis實現分布式多規則限流的方式介紹

鴻蒙OS 分布式任務調度
什么是分布式架構?




 關于正態分布和貝塔分布的案例介紹
關于正態分布和貝塔分布的案例介紹











評論