堆其實就是一種特殊的隊列——優先隊列。
普通的隊列游戲規則很簡單:就是先進先出;但這種優先隊列搞特殊,不是按照進隊列的時間順序,而是按照每個元素的優先級來比拼,優先級高的在堆頂。
這也很容易理解吧,比如各種軟件都有會員制度,某軟件用了會員就能加速下載的,不同等級的會員速度還不一樣,那就是優先級不同呀。
還有其實每個人回復微信消息也是默默的把消息放進堆里排個序:先回男朋友女朋友的,然后再回其他人的。
這里要區別于操作系統里的那個“堆”,這兩個雖然都叫堆,但是沒有半毛錢關系,都是借用了Heap這個英文單詞而已。
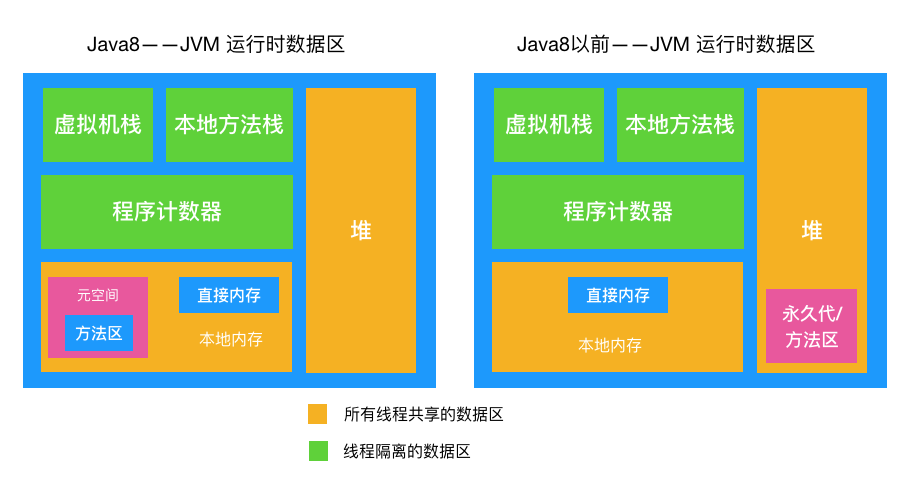
我們再來回顧一下「堆」在整個Java集合框架中的位置:
也就是說,
PriorityQueue是一個類(class);
PriorityQueue繼承自Queue這個接口(Interface);
那heap在哪呢?
heap其實是一個抽象的數據結構,或者說是邏輯上的數據結構,并不是一個物理上真實存在的數據結構。
heap其實有很多種實現方式,比如binomialheap,Fibonacciheap等等。但是面試最常考的,也是最經典的,就是binaryheap二叉堆,也就是用一棵完全二叉樹來實現的。
那完全二叉樹是怎么實現的?
其實是用數組來實現的!
所以binaryheap/PriorityQueue實際上是用數組來實現的。
這個數組的排列方式有點特別,因為它總會維護你定義的(或者默認的)優先級最高的元素在數組的首位,所以不是隨便一個數組都叫「堆」,實際上,它在你心里,應該是一棵「完全二叉樹」。
這棵完全二叉樹,只存在你心里和各大書本上;實際在在內存里,哪有什么樹?就是數組罷了。
那為什么完全二叉樹可以用數組來實現?是不是所有的樹都能用數組來實現?
這個就涉及完全二叉樹的性質了,我們下一篇會細講,簡單來說,因為完全二叉樹的定義要求了它在層序遍歷的時候沒有氣泡,也就是連續存儲的,所以可以用數組來存放;第二個問題當然是否。
堆的特點
堆是一棵完全二叉樹;
堆序性(heaporder):任意節點都優于它的所有孩子。
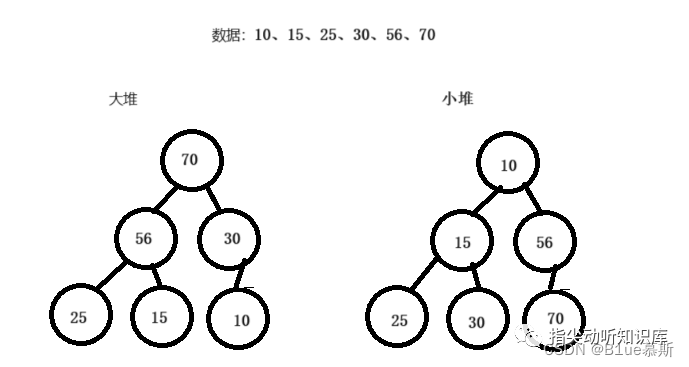
a.如果是任意節點都大于它的所有孩子,這樣的堆叫大頂堆,MaxHeap;
b.如果是任意節點都小于它的所有孩子,這樣的堆叫小頂堆,MinHeap;
左圖是小頂堆,可以看出對于每個節點來說,都是小于它的所有孩子的,注意是**所有孩子,包括孫子,曾孫...**
既然堆是用數組來實現的,那么我們可以找到每個節點和它的父母/孩子之間的關系,從而可以直接訪問到它們。
比如對于節點3來說,
它的Index=1,
它的parentindex=0,
左孩子leftchildindex=3,
右孩子rightchildindex=4.
可以歸納出如下規律:
設當前節點的index=x,
那么parentindex=(x-1)/2,
左孩子leftchildindex=2*x+1,
右孩子rightchildindex=2*x+2.
有些書上可能寫法稍有不同,是因為它們的數組是從1開始的,而我這里數組的下標是從0開始的,都是可以的。
這樣就可以從任意一個點,一步找到它的孫子、曾孫子,真的太方便了,在之后講具體操作時大家可以更深刻的體會到。
那有關堆的基本操作,以及為什么heapify()是O(n)的,我們之后再聊。
編輯:hfy
-
JAVA
+關注
關注
19文章
2970瀏覽量
104809 -
堆棧
+關注
關注
0文章
182瀏覽量
19779 -
隊列
+關注
關注
1文章
46瀏覽量
10911
發布評論請先 登錄
相關推薦
java集合干貨系列
什么是橋堆,橋堆的作用是什么?
整流堆,什么是整流堆
明確區分堆與棧,堆和棧究竟有什么區別?

什么是堆內存?堆內存是如何分配的?
整流橋堆的作用和原理圖
橋堆的作用是什么?橋堆整流后電壓是多少?
jvm配置堆內存初始值參數
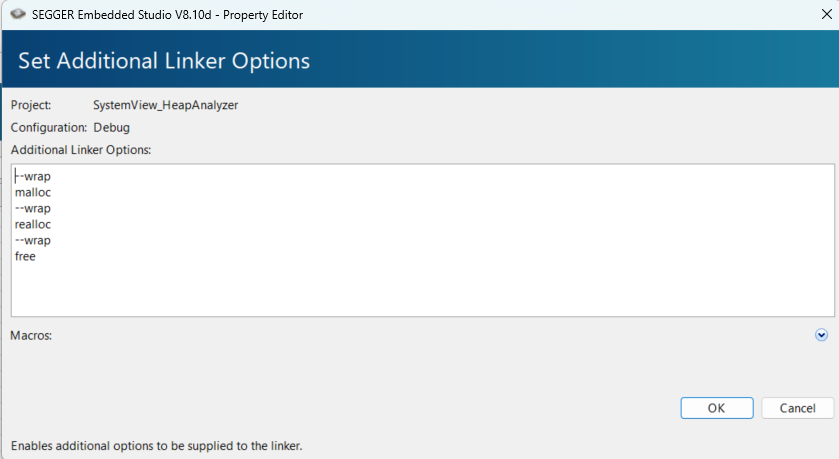
如何使用SystemView的堆監控功能




 什么是堆,堆在整個Java集合框架中的作用
什么是堆,堆在整個Java集合框架中的作用










評論