本文選自《物理》2020年第9期
01 理論背景
在經(jīng)典世界中,物體都擁有豐富的屬性,如質(zhì)量、體積等等。可以說(shuō),正是對(duì)這些屬性的認(rèn)識(shí)和描述,在人們腦海中形成各種各樣客觀實(shí)在的物理圖像。對(duì)客觀存在的物體的各種屬性及其相互聯(lián)系和運(yùn)動(dòng)規(guī)律的研究,構(gòu)成了我們今天的物理學(xué)。直覺(jué)告訴我們,物理本體與其擁有的屬性是不可分離的[1]。然而,這個(gè)直覺(jué)源自對(duì)經(jīng)典世界中物理客體的認(rèn)識(shí),并嚴(yán)重依賴于經(jīng)典物理圖像。當(dāng)我們將視角聚焦到微觀尺度,研究半徑只有不到一個(gè)皮米(10-12m)的電子或是波長(zhǎng)不到一個(gè)微米(10-6m)的光子時(shí),情況就變得有所不同。2013年有理論研究認(rèn)為,微觀粒子的物理屬性(如電子的電荷和自旋、光子的偏振等)可以和其本體分離,這種現(xiàn)象被沃爾夫獎(jiǎng)獲得者阿哈羅諾夫等人稱之為“量子柴郡貓”(quantum Cheshire cat)[2]。
02 弱測(cè)量與弱值
為了揭示微觀世界中的“量子柴郡貓”現(xiàn)象,需要使用有別于傳統(tǒng)量子測(cè)量的手段,也就是量子弱測(cè)量技術(shù)。這里之所以被冠以“弱”,是相對(duì)于傳統(tǒng)量子測(cè)量表現(xiàn)出的“強(qiáng)”而言的。在傳統(tǒng)的量子測(cè)量理論中,測(cè)量用可觀測(cè)量算符表示[3]。對(duì)描述微觀系統(tǒng)的波函數(shù)實(shí)施的量子測(cè)量,會(huì)將系統(tǒng)隨機(jī)坍縮到測(cè)量算符的某一個(gè)本征態(tài)[4],這個(gè)過(guò)程將不可避免地破壞量子系統(tǒng)的狀態(tài)。例如使用檢偏器對(duì)光子的偏振狀態(tài)進(jìn)行鑒定,盡管最終能夠確定光子的偏振方向,但同時(shí)也會(huì)完全破壞初始狀態(tài),除非光子一開(kāi)始就處在檢偏器的本征指向上。在該測(cè)量過(guò)程中,正是由于需要完成待測(cè)量子系統(tǒng)和測(cè)量探針之間足夠強(qiáng)的耦合,以至于能將系統(tǒng)和探針完全糾纏起來(lái),我們將其稱之為強(qiáng)測(cè)量。
與之相對(duì)應(yīng),量子弱測(cè)量則考慮另外一種情況,那就是系統(tǒng)和探針之間的耦合非常微弱,以至于被測(cè)系統(tǒng)和探針仍然處于接近獨(dú)立的狀態(tài)。如此弱的耦合不會(huì)對(duì)系統(tǒng)造成演化過(guò)程的過(guò)分干擾,系統(tǒng)還可以繼續(xù)完成后續(xù)相干演化,但同時(shí)弱測(cè)量也不會(huì)提供關(guān)于系統(tǒng)狀態(tài)的確定性信息。作為量子力學(xué)中一個(gè)比較古老的話題,直到弱值概念被提出后,弱測(cè)量才開(kāi)始受到應(yīng)有的關(guān)注[5]。和量子強(qiáng)測(cè)量中定義可觀測(cè)量的期望值一樣,可觀測(cè)量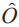 的弱值被定義在前選擇態(tài)
的弱值被定義在前選擇態(tài)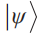 和后選擇態(tài)
和后選擇態(tài)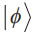 上,由兩者共同決定,即
上,由兩者共同決定,即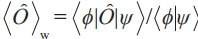 。但有別于傳統(tǒng)期望值,弱值并不局限于在可觀測(cè)量本征值上進(jìn)行取值,可以遠(yuǎn)超過(guò)這個(gè)范圍,甚至可以取復(fù)數(shù)值。無(wú)論是面向量子信息開(kāi)發(fā)新技術(shù)還是探索量子力學(xué)基本問(wèn)題,弱測(cè)量和弱值的概念都被廣泛采用:在技術(shù)層面,如開(kāi)發(fā)基于白光源的高精度時(shí)間延遲測(cè)量[6,7],以及直接表征糾纏系統(tǒng)波函數(shù)[8]等;而在基礎(chǔ)研究層面,如重構(gòu)微觀粒子的玻姆軌跡[9],以及觀測(cè)楊氏雙縫中非局域的動(dòng)量傳遞[10]等。?
。但有別于傳統(tǒng)期望值,弱值并不局限于在可觀測(cè)量本征值上進(jìn)行取值,可以遠(yuǎn)超過(guò)這個(gè)范圍,甚至可以取復(fù)數(shù)值。無(wú)論是面向量子信息開(kāi)發(fā)新技術(shù)還是探索量子力學(xué)基本問(wèn)題,弱測(cè)量和弱值的概念都被廣泛采用:在技術(shù)層面,如開(kāi)發(fā)基于白光源的高精度時(shí)間延遲測(cè)量[6,7],以及直接表征糾纏系統(tǒng)波函數(shù)[8]等;而在基礎(chǔ)研究層面,如重構(gòu)微觀粒子的玻姆軌跡[9],以及觀測(cè)楊氏雙縫中非局域的動(dòng)量傳遞[10]等。?
03 概念提出與實(shí)驗(yàn)驗(yàn)證
回到如何揭示“量子柴郡貓”這個(gè)問(wèn)題,在其最初版本中,阿哈羅諾夫等人考慮將光子作為“量子柴郡貓”,并且將光子的自旋(偏振)作為其笑臉[2]。簡(jiǎn)化示意如圖1所示,其中包括分束器、反射鏡及探測(cè)器等。整個(gè)系統(tǒng)由一個(gè) Mach—Zehnder 干涉儀構(gòu)成,其中光子在經(jīng)過(guò)分束鏡后,可以選擇上下兩個(gè)路徑。我們可以通過(guò)對(duì)光子實(shí)施兩組弱測(cè)量來(lái)揭示光子本體和其屬性的分離,其中一組用于測(cè)量光子本體所處的位置(用路徑可觀測(cè)量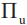 ,
,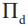 表示),另一組則用于測(cè)量其自旋狀態(tài),也就是柴郡貓的笑臉(用條件自旋可觀測(cè)量
表示),另一組則用于測(cè)量其自旋狀態(tài),也就是柴郡貓的笑臉(用條件自旋可觀測(cè)量 ,
, 表示),測(cè)量結(jié)果則由相應(yīng)的弱值描述。當(dāng)某個(gè)路徑可觀測(cè)量的弱值為1時(shí),表明光子本體出現(xiàn)在相應(yīng)的路徑當(dāng)中,取值為0則表明光子本體未處于相應(yīng)的路徑當(dāng)中;類似地,條件自旋投影子的弱值為 1/0?則表明光子的自旋(笑臉)出現(xiàn)/未出現(xiàn)在相應(yīng)的路徑中。阿哈羅諾夫等人指出,通過(guò)精巧設(shè)置合適的前后選擇態(tài),就有可能展現(xiàn)類似《愛(ài)麗絲夢(mèng)游仙境》中柴郡貓與其笑臉?lè)蛛x的現(xiàn)象[11]。具體來(lái)說(shuō),在 Mach—Zehnder 干涉儀的上路徑中,對(duì)路徑及條件自旋觀測(cè)量實(shí)施的弱測(cè)量給出相應(yīng)的弱值分別為0和1,也就是說(shuō),有一只沒(méi)有貓的笑臉出現(xiàn)在該路徑中。相應(yīng)的,在下路徑中實(shí)施的弱測(cè)量得到的弱值分別為1和0,也就是說(shuō),下路徑中出現(xiàn)了一只缺少了笑臉的貓。簡(jiǎn)而言之,在干涉儀中“量子柴郡貓”和它的笑臉被分開(kāi)了。
表示),測(cè)量結(jié)果則由相應(yīng)的弱值描述。當(dāng)某個(gè)路徑可觀測(cè)量的弱值為1時(shí),表明光子本體出現(xiàn)在相應(yīng)的路徑當(dāng)中,取值為0則表明光子本體未處于相應(yīng)的路徑當(dāng)中;類似地,條件自旋投影子的弱值為 1/0?則表明光子的自旋(笑臉)出現(xiàn)/未出現(xiàn)在相應(yīng)的路徑中。阿哈羅諾夫等人指出,通過(guò)精巧設(shè)置合適的前后選擇態(tài),就有可能展現(xiàn)類似《愛(ài)麗絲夢(mèng)游仙境》中柴郡貓與其笑臉?lè)蛛x的現(xiàn)象[11]。具體來(lái)說(shuō),在 Mach—Zehnder 干涉儀的上路徑中,對(duì)路徑及條件自旋觀測(cè)量實(shí)施的弱測(cè)量給出相應(yīng)的弱值分別為0和1,也就是說(shuō),有一只沒(méi)有貓的笑臉出現(xiàn)在該路徑中。相應(yīng)的,在下路徑中實(shí)施的弱測(cè)量得到的弱值分別為1和0,也就是說(shuō),下路徑中出現(xiàn)了一只缺少了笑臉的貓。簡(jiǎn)而言之,在干涉儀中“量子柴郡貓”和它的笑臉被分開(kāi)了。
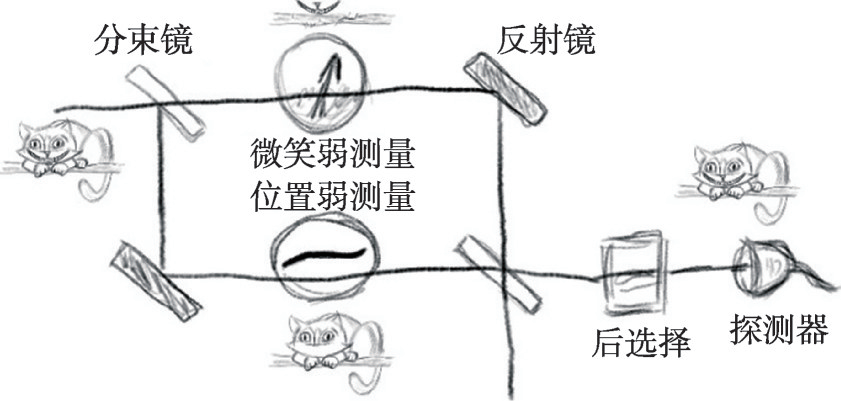
圖1 由 Mach—Zehnder 干涉儀構(gòu)成,揭示“量子柴郡貓”效應(yīng)的示意圖
在“量子柴郡貓”的概念被提出后不久,來(lái)自?shī)W地利維也納科技大學(xué)的實(shí)驗(yàn)物理學(xué)家便利用中子進(jìn)行了實(shí)驗(yàn)演示[12]。他們通過(guò)在中子干涉儀中外加磁場(chǎng),精確調(diào)控中子的自旋和路徑的量子狀態(tài),從而實(shí)現(xiàn)了前選擇態(tài)的制備以及后選擇的操作。在干涉儀的兩臂中施加弱測(cè)量獲得所需要的中子路徑及條件自旋的弱值。實(shí)驗(yàn)結(jié)果正如阿哈羅諾夫等人所預(yù)言的那樣,在干涉儀中,中子的自旋總是出現(xiàn)在與其本體位置相反的另一臂。緊接著,美國(guó)波特蘭大學(xué)的實(shí)驗(yàn)物理學(xué)家使用自發(fā)參量下轉(zhuǎn)換過(guò)程產(chǎn)生的可預(yù)報(bào)單光子進(jìn)行了類似的實(shí)驗(yàn),同樣看到了“量子柴郡貓”現(xiàn)象[13]。
04 缺陷與爭(zhēng)議
這些實(shí)驗(yàn)進(jìn)展表明,不論是有質(zhì)量的中子還是無(wú)質(zhì)量的光子,都能展現(xiàn)出這種不符合常理卻真實(shí)存在的量子現(xiàn)象。然而,利用光子進(jìn)行的實(shí)驗(yàn)備受爭(zhēng)議,因?yàn)檫@種現(xiàn)象在基于經(jīng)典光的干涉儀中同樣能夠觀察到,并且這樣的實(shí)驗(yàn)可以用描述電磁波的經(jīng)典波動(dòng)理論予以解釋[14]。因此,“量子柴郡貓”在多大程度上是屬于量子世界,這一問(wèn)題亟需得到確認(rèn)。另一方面,既有實(shí)驗(yàn)盡管展示了微觀粒子在演化過(guò)程中可以處于本體與屬性的分離,但是最終它們?nèi)匀痪酆系搅艘黄稹<热晃锢韺傩钥梢詮钠浔倔w分離,隨之也自然會(huì)帶來(lái)如下問(wèn)題:物理客體是否可以攜帶本不屬于自己的物理屬性呢[15]?因此,進(jìn)行更為復(fù)雜的實(shí)驗(yàn)進(jìn)一步展示“量子柴郡貓”的獨(dú)特量子效應(yīng),例如實(shí)現(xiàn)涉及多個(gè)“量子柴郡貓”笑臉的交換,可以從正面回答這兩方面的爭(zhēng)議,對(duì)理解量子系統(tǒng)如何從根本上區(qū)別于其經(jīng)典對(duì)應(yīng)具有重要的物理意義。
05 笑臉的隔空交換
然而,嘗試觀察“量子柴郡貓”的笑臉交換并不容易,這涉及到對(duì)多體量子系統(tǒng)弱值提取的難題[16—18]。提取弱值的通常做法是引入輔助探針,當(dāng)系統(tǒng)增大時(shí),所需的耦合過(guò)程將會(huì)越來(lái)越復(fù)雜。想要實(shí)現(xiàn)光子偏振的無(wú)接觸交換,勢(shì)必涉及多個(gè)“量子柴郡貓”,進(jìn)一步在系統(tǒng)中引入額外探針面臨技術(shù)挑戰(zhàn)。我們經(jīng)過(guò)理論研究發(fā)現(xiàn),通過(guò)對(duì)系統(tǒng)施加微擾,可以繞過(guò)傳統(tǒng)的弱測(cè)量方法,利用系統(tǒng)探測(cè)概率與微擾強(qiáng)度之間的內(nèi)在聯(lián)系,直接得到所需要的弱值[19]。此外,我們還發(fā)現(xiàn)獲得弱值所需的微擾形式,與數(shù)學(xué)中的虛數(shù)概念有著深刻的聯(lián)系。在量子力學(xué)中,一個(gè)封閉體系的演化遵循薛定諤方程,時(shí)間是演化的一個(gè)參數(shù)。如果將演化的時(shí)間取為一個(gè)絕對(duì)值很小的虛數(shù),對(duì)應(yīng)的微擾將使體系不再封閉,但是這種演化恰好可以將光子最后被測(cè)量的概率與演化的時(shí)間聯(lián)系起來(lái),在兩者之間建立一個(gè)線性的關(guān)系。這個(gè)線性模型的斜率就剛好給出弱值,而相應(yīng)的微擾被稱之為虛時(shí)演化[20]。
圖2 實(shí)現(xiàn)“量子柴郡貓”笑臉交換的實(shí)驗(yàn)裝置。包括3個(gè)模塊:基于自發(fā)參量下轉(zhuǎn)換的雙光子超糾纏態(tài)制備,使用平行偏振分束器實(shí)現(xiàn)條件自旋可觀測(cè)量弱測(cè)量的裝置,以及實(shí)現(xiàn)笑臉交換的雙光子干涉光路(改編自文獻(xiàn)[19])
如圖2所示,我們首先通過(guò)自發(fā)參量下轉(zhuǎn)換過(guò)程,制備出不存在經(jīng)典描述的雙光子超糾纏態(tài),也就是兩個(gè)光子的偏振和路徑自由度分別處于最大糾纏態(tài),但是兩個(gè)維度之間處于毫無(wú)關(guān)聯(lián)的直積狀態(tài)。進(jìn)一步通過(guò)在路徑和自旋上施加一些精確的受控操作,將雙光子制備到特定圖態(tài),完成前選擇態(tài)的制備。緊接著,我們通過(guò)在光路中引入虛時(shí)演化,實(shí)現(xiàn)對(duì)光子路徑和條件自旋的弱測(cè)量。在實(shí)驗(yàn)的最后,通過(guò)實(shí)施一種被稱為聯(lián)合貝爾態(tài)測(cè)量的操作,完成對(duì)系統(tǒng)的后選擇。我們通過(guò)對(duì)不同的微擾種類和演化時(shí)間下光子探測(cè)效率地分析,最終獲得了光子的路徑和條件偏振可觀測(cè)量的弱值。實(shí)驗(yàn)的主要結(jié)果如圖3所示。這些弱值表明,實(shí)驗(yàn)中的兩光子都展現(xiàn)出本體和屬性分離的“量子柴郡貓”現(xiàn)象。更為重要的是,最終每只量子柴郡貓都會(huì)捕獲另一只貓的偏振屬性。這個(gè)新捕獲的偏振替代了光子原先的偏振屬性,隨著光子最終進(jìn)入探測(cè)器而被檢測(cè)到,最終實(shí)現(xiàn)光子本體與其初始時(shí)刻攜帶的自旋屬性的永久分離。
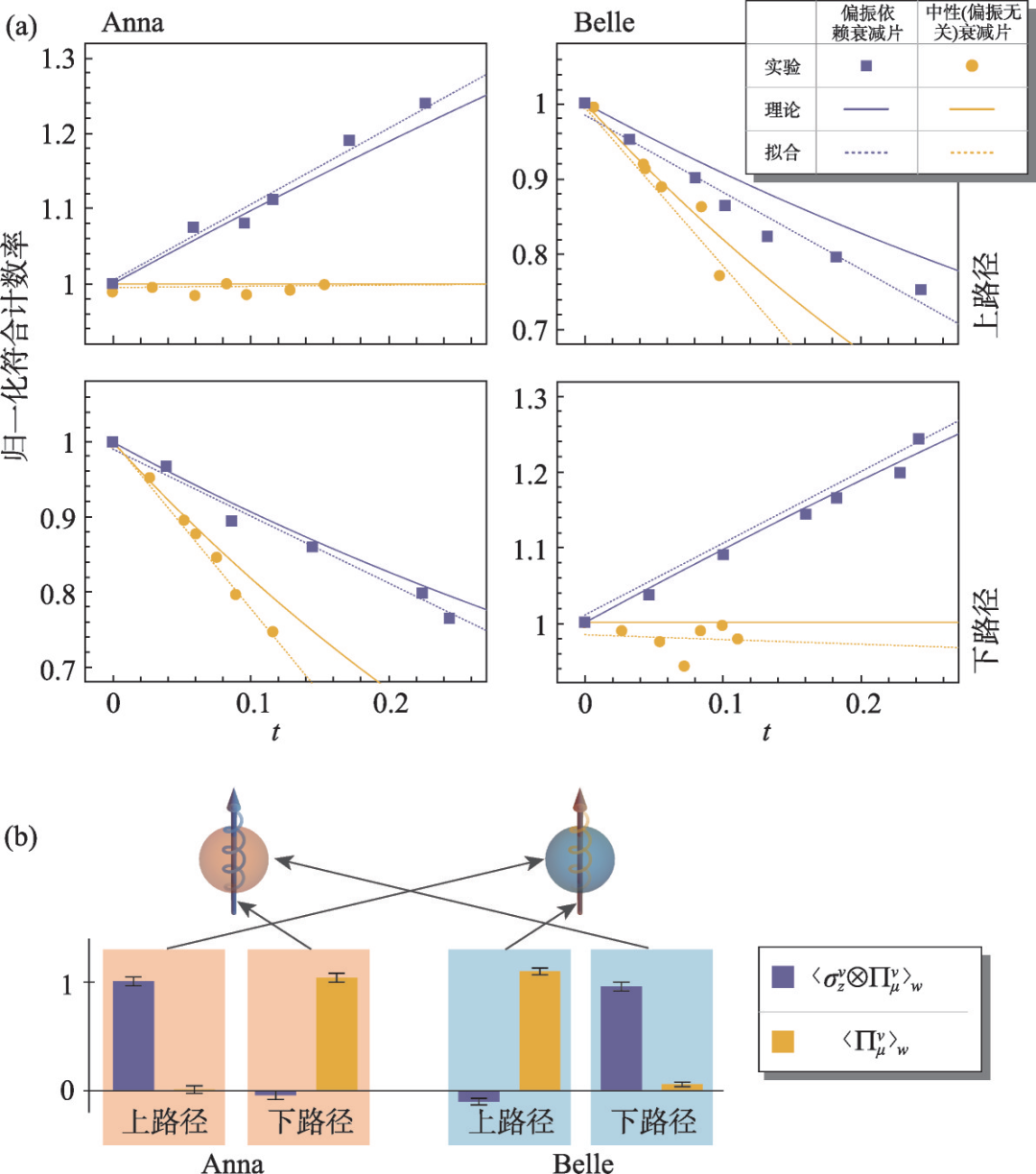
圖3 歸一化符合計(jì)數(shù)隨耦合時(shí)間線性變化(a),其斜率給出相應(yīng)可觀測(cè)量的弱值(b)。其中Anna和Belle是兩只柴郡貓的名字(改編自文獻(xiàn)[19])
該研究成果最近發(fā)表在《自然·通訊》[19]。實(shí)現(xiàn)多個(gè)“量子柴郡貓”的笑臉交換,展示了量子世界中物質(zhì)與其屬性的靈活多變的關(guān)系,對(duì)探索微觀粒子的性質(zhì)在接受測(cè)量之前是否具有實(shí)在性(真實(shí),reality)具有啟發(fā)意義,將對(duì)量子力學(xué)基礎(chǔ)問(wèn)題的研究起到重要推動(dòng)作用。另一方面,通過(guò)引入微擾獲得弱值,從而規(guī)避傳統(tǒng)方法對(duì)額外輔助探針的需求,也將成為解決量子科學(xué)領(lǐng)域其他難題的有力工具。
參考文獻(xiàn)
[1] Bancal J D. Nat. Phys.,2013,10:11
[2] Aharonov Y,Popescu S,Rohrlich D et al. New J. Phys.,2013,15:113015
[3] Griffiths D J. Introduction to quantum mechanics. Cambridge University Press,2016
[4] von Neumann J. Mathematical foundations of quantum mechanics. Princeton University Press,2018
[5] Aharonov Y,Albert D Z,Vaidman L. Phys. Rev. Lett.,1988,60:1351
[6] Xu X Y,Kedem Y,Sun K et al. Phys. Rev. Lett.,2013,111:033604
[7] Li C F,Xu X Y,Tang J S et al. Phys. Rev. A,2011,83:044102
[8] Pan W W,Xu X Y,Kedem Y et al. Phys. Rev. Lett.,2019,123:150402
[9] Xiao Y,Kedem Y,Xu J S et al. Opt. Express,2017,25:14463
[10] Xiao Y,Wiseman H M,Xu J S et al. Sci. Adv.,2019,5:eaav9547
[11] Carroll L. Alice's adventures in wonderland. Broadview Press,1865
[12] Denkmayr T,Geppert H,Sponar S et al. Nat. Commun.,2014,5:4492
[13] Ashby J M,Schwarz P D,Schlosshauer M. Phys. Rev. A,2016,94:012102
[14] Atherton D P,Ranjit G,Geraci A A et al. Opt. Lett.,2015,40:879
[15] Das D,Pati A K. New J. Phys.,2020,22:063032
[16] Kedem Y,Vaidman L. Phys. Rev. Lett.,2010,105:230401
[17] Xu X Y,Pan W W,Wang Q Q et al. Phys. Rev. Lett.,2019,122:100405
[18] Xu X Y,Pan W W,Kedem Y et al. Opt. Lett.,2020,45:1715
[19] Liu Z H,Pan W W,Xu X Y et al. Nat. Commun.,2020,11:3006
[20] Xu J S,Yung M H,Xu X Y et al. Nat. Photonics,2014,8:113
責(zé)任編輯:xj
原文標(biāo)題:兩只“量子柴郡貓”笑臉的無(wú)接觸交換
文章出處:【微信公眾號(hào):中科院半導(dǎo)體所】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
-
量子
+關(guān)注
關(guān)注
0文章
489瀏覽量
25763 -
光子
+關(guān)注
關(guān)注
0文章
115瀏覽量
14694
原文標(biāo)題:兩只“量子柴郡貓”笑臉的無(wú)接觸交換
文章出處:【微信號(hào):bdtdsj,微信公眾號(hào):中科院半導(dǎo)體所】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
面向未來(lái)量子通信與大物理研究線上研討會(huì)QA筆記請(qǐng)查收!
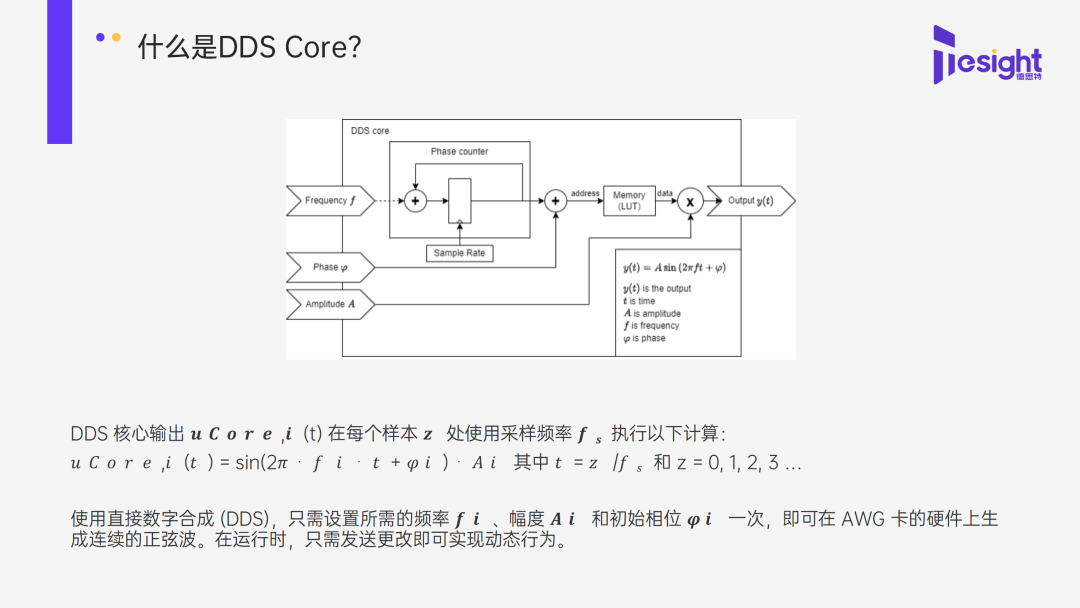
ADS1232在第9、第10腳即接104電容的兩端用數(shù)字萬(wàn)用表,測(cè)不到電壓值,是0伏,為什么?
格陸博科技第100萬(wàn)只ESC量產(chǎn)下線
量子通信與量子計(jì)算的關(guān)系
量子通信技術(shù)的應(yīng)用 量子通信與傳統(tǒng)通信的區(qū)別
菱形石墨烯結(jié)構(gòu)及其中的量子反常霍爾效應(yīng)
玻色量子亮相2024年《國(guó)家科學(xué)評(píng)論》物理與信息科學(xué)前沿論壇
柴暖改裝遠(yuǎn)程
NVIDIA 助力谷歌量子 AI 通過(guò)量子器件物理學(xué)模擬加快處理器設(shè)計(jì)

《量子計(jì)算觀察》智庫(kù)報(bào)告第1期:未來(lái)5年“量超融合”黃金期 3大商機(jī)將現(xiàn)

積鼎科技攜手濰柴動(dòng)力的噴嘴霧化模擬項(xiàng)目榮獲2024年數(shù)字仿真卓越應(yīng)用獎(jiǎng)

推挽電路如何使兩只管子都關(guān)斷
《圖說(shuō)本源產(chǎn)品》系列之二:量子計(jì)算全物理體系學(xué)習(xí)機(jī)

【《計(jì)算》閱讀體驗(yàn)】量子計(jì)算
連做兩只機(jī)器狗,終于拿捏了這些算法……



















評(píng)論