軟件度量是對軟件開發(fā)項目、過程及其產品進行數(shù)據(jù)定義、收集以及分析的持續(xù)性定量化過程,目的在于對此加以理解、預測、評估、控制和改善,從而保證軟件開發(fā)中的高效率、低成本、高質量。但是,得到正確的度量只是測量程序的一部分。軟件質量是與所收集和分析的數(shù)據(jù)質量密切相關的,數(shù)據(jù)清洗過程的目的就是要解決“臟數(shù)據(jù)”的問題。數(shù)據(jù)清洗是指去除或修補源數(shù)據(jù)中的不完整、不一致、含噪聲的數(shù)據(jù)。在源數(shù)據(jù)中,可能由于疏忽、懶惰,甚至為了保密使系統(tǒng)設計人員無法得到某些數(shù)據(jù)項的數(shù)據(jù)。根據(jù)決策系統(tǒng)中“garbage in garbage out”(如果輸入的分析數(shù)據(jù)是垃圾則輸出的分析結果也將是垃圾)原理,必須處理這些噪聲數(shù)據(jù)。去掉噪聲平滑數(shù)據(jù)的技術主要有分箱(binning)、聚類(clustering)、回歸(regression)等。本文在回歸分析的基礎上,加入了盒形圖進行數(shù)據(jù)過濾,從而得出一條線性回歸直線,使模式或者關系變得更加明顯,從而用這些模式和關系對測量的屬性作出判斷。
1 盒形圖和回歸分析簡介
1.1 盒形圖
該方法可以描述數(shù)據(jù)集取值范圍的情況,展示數(shù)據(jù)主要聚集的區(qū)域,發(fā)現(xiàn)離群數(shù)據(jù)可能的位置,以便于對離群數(shù)據(jù)進行處理。盒形圖顯示一個變量的信息,如對相同 CMM等級的不同項目完成每個FP的工作量分析,根據(jù)中位數(shù)m、上四分位數(shù)u、下四分位數(shù)l、盒長d、和尾(tail)來分析。
中位數(shù)是在數(shù)據(jù)集中排列居中的項。也就是說,如果中位數(shù)取值為m,則數(shù)據(jù)集中有一半的值大于m,一半的值小于m。將所有數(shù)值按大小順序排列并分成四等份,處于三個分割點位置的得分就是四分位數(shù)。最小的四分位數(shù)稱為下四分位數(shù)l,所有數(shù)值中,有四分之一小于下四分位數(shù),四分之三大于下四分位數(shù)。中點位置的四分位數(shù)就是中位數(shù)。最大的四分位數(shù)稱為上四分位數(shù)u,所有數(shù)值中,有四分之三小于上四分位數(shù),四分之一大于上四分位數(shù)。也有叫第25百分位數(shù)、第75百分位數(shù)的。將上四分位數(shù)和下四分位數(shù)的距離定義為盒長d,因此,d=u-l。接下來定義分布的尾(tail)。理論上,上尾值點為u+1.5d,下尾值為 u-1.5d,這些值必須進行舍位處理,以接近真實數(shù)據(jù),位于上尾和下尾之外的值稱為離群值。
1.2 回歸分析方法
回歸分析方法是研究要素之間具體數(shù)量關系的強有力的工具,運用這種方法能夠建立反映要素之間具體的數(shù)量關系的數(shù)學模型,即回歸模型。線性回歸技術的基礎就是散點圖。將每個屬性對表示為一個數(shù)據(jù)點(x,y),然后用回歸技術計算出能夠最好地擬合這些點的直線。目標是將屬性y(因變量)根據(jù)屬性x(自變量)表示為等式:y=a+bx。
線性回歸的理論是從每個點垂直向上或向下畫一條線段到趨勢直線,表示從數(shù)據(jù)點到趨勢直線的垂直距離。在某種意義上,這些線段的長度表示數(shù)據(jù)和直線的差異,且這種差異應盡可能地小。因此,“最佳擬合”的直線式是指使該距離最小的直線。
在數(shù)學上要計算“最佳擬合”直線的斜率b和截距a是很簡單的。每個點的差異稱為殘差,生成線性回歸直線的公式是殘差的平方和達到最小。可以將每個數(shù)據(jù)點的殘差表示為:
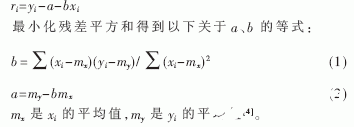
2 算法實現(xiàn)
在進行數(shù)據(jù)清洗時,由于數(shù)據(jù)是無序輸入的,所以先對其排序,再用盒形圖法行數(shù)據(jù)清洗。以下是偽代碼:
voidBubbleSort(doublem,doubleq,intn)//先對輸入
//的數(shù)據(jù)進行冒泡排序,并相應修改
//第二組數(shù)據(jù)的順序,以保證它們之間的對應關系
{for(inti=0;i<n;i++)
for(intj=n-1;j>i;j--)
{
輸入數(shù)據(jù)的排序
修改第二組數(shù)據(jù)
}
}
voidbox(double*m,double*q,int&n)//盒形法篩選
//掉離群項目工作量數(shù)據(jù),n為輸入數(shù)據(jù)個數(shù),m、q為指針
{
doublea,b,c,top,bottom,l;//上分位a,中位數(shù)b,//下分位c
if(n%2==0)//計算出3個四分位數(shù)
{
b=(*(m+n/2)+*(m+n/2-1))/2;//數(shù)據(jù)個數(shù)為
//偶數(shù)時,中位數(shù)取中間兩數(shù)的平均值
a=*(m+n/4);
c=*(m+3*n/4);}
}
else
{b=*(m+n/2);
a=*(m+n/4);
c=*(m+3*n/4);}
l=c-a;top=c+1.5*l;bottom=c-1.5*l;//計算出盒
//長,上尾數(shù),下尾數(shù)
if(bottom<0)bottom=m;//并進行必要的舍位處理
intj=n;
for(inti=0;i<j;i++)//判斷是否為離群值,
{
if(*(m+i)>top‖*(m+i)<bottom)
如有,將其從數(shù)組中剔去
}
}
接下來要對篩選出來的數(shù)據(jù)進行回歸分析,從而得到一個數(shù)據(jù)模型。
voidregress(double*m,double*q,intn)//對數(shù)組
//m和數(shù)據(jù)q的數(shù)據(jù)用線性回歸法進行擬合
//并用一條直線表示出它們之間的對應關系
{doubleaverage_m,average_q,total_m,total_q,L_mq,L_mm;
doublea,b;//擬合直線y=a+bx的2個待定系數(shù)
for(inti=0;i<n;i++)。
{
//計算兩組數(shù)據(jù)的和total_m和total_q
}
average_m=total_m/n;//求的第一組數(shù)據(jù)的平均值
average_q=total_q/n;//求的第二組數(shù)據(jù)的平均值
for(intj=0;j<n;j++)
{
利用公式(1)計算兩組數(shù)據(jù)m,q它們所有數(shù)據(jù)偏離程度的對應相乘之和L_mq
}
for(intk=0;k<n;k++)
{
計算第一組數(shù)據(jù)m,它的所有數(shù)據(jù)偏離
程度的平方和L_mm
}
b=L_mq/L_mm;//計算出擬合直線的待定系數(shù)
//b的擬合值
a=average_q-b*average_m;//利用公式(2)算出參
//數(shù)a
}
從而得到一條線性直線,算法結束。
3 算法在實驗數(shù)據(jù)上的實現(xiàn)
從SSMBSS(上海軟件度量基準體系)中選取了一組數(shù)據(jù)(見表1),首先將其用散點圖列出來(見圖1),然后用盒形圖進行數(shù)據(jù)清洗(見圖2),最后用回歸分析得出擬合直線(見圖3)。
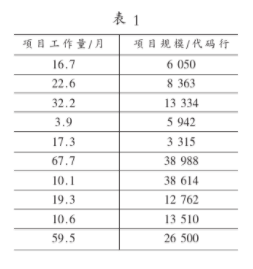
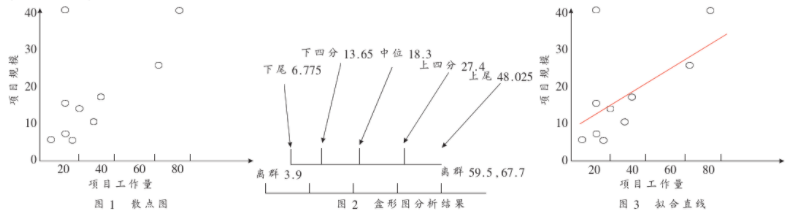
綜上所述,對于軟件度量過程中出現(xiàn)的數(shù)據(jù)冗余和失真的情況,可以通過數(shù)據(jù)過濾和回歸分析進行處理,除去那些離群的數(shù)據(jù),并得出相應的擬合直線,這樣就可以分析出數(shù)據(jù)的規(guī)律,保證軟件的質量,提高效率。
責任編輯:gt
-
數(shù)據(jù)
+關注
關注
8文章
7002瀏覽量
88943 -
軟件
+關注
關注
69文章
4921瀏覽量
87403 -
回歸分析
+關注
關注
0文章
7瀏覽量
5898
發(fā)布評論請先 登錄
相關推薦
《Visual C# 2008程序設計經(jīng)典案例設計與實現(xiàn)》---餅形圖表分析圖
python數(shù)據(jù)分析基礎之使用statasmodels進行線性回歸
回歸算法有哪些,常用回歸算法(3種)詳解
數(shù)學建模與數(shù)學實驗-回歸分析
過程間指針分析算法的改進
信息過濾系統(tǒng)中字符串匹配算法的研究
RFID中間件數(shù)據(jù)的過濾方法的研究和分析
基于高強度密碼S盒安全性分析
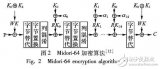
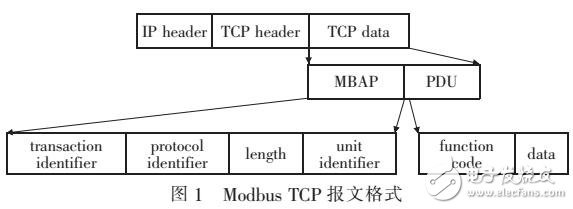
基于Modbus功能碼細粒度過濾算法的研究
如何使用IFS分形算法進行樹木形態(tài)的分析和實現(xiàn)
matlab經(jīng)典算法數(shù)字實驗教程之回歸分析





 基于盒形圖和回歸分析實現(xiàn)數(shù)據(jù)過濾算法的研究分析
基于盒形圖和回歸分析實現(xiàn)數(shù)據(jù)過濾算法的研究分析










評論