經常有讀者問區間相關的問題，今天寫一篇文章，秒殺三道區間相關的問題。

所謂區間問題，就是線段問題，讓你合并所有線段、找出線段的交集等等。主要有兩個技巧：

1、排序。常見的排序方法就是按照區間起點排序，或者先按照起點升序排序，若起點相同，則按照終點降序排序。當然，如果你非要按照終點排序，無非對稱操作，本質都是一樣的。

2、畫圖。就是說不要偷懶，勤動手，兩個區間的相對位置到底有幾種可能，不同的相對位置我們的代碼應該怎么去處理。

廢話不多說，下面我們來做題。

區間覆蓋問題

這是力扣第 1288 題，看下題目：

題目問我們，去除被覆蓋區間之后，還剩下多少區間，那么我們可以先算一算，被覆蓋區間有多少個，然后和總數相減就是剩余區間數。

對于這種區間問題，如果沒啥頭緒，首先排個序看看，比如我們按照區間的起點進行升序排序：

排序之后，兩個相鄰區間可能有如下三種相對位置：

對于這三種情況，我們應該這樣處理：

對于情況一，找到了覆蓋區間。

對于情況二，兩個區間可以合并，成一個大區間。

對于情況三，兩個區間完全不相交。

依據幾種情況，我們可以寫出如下代碼：

intremoveCoveredIntervals(int[][]intvs){ //按照起點升序排列，起點相同時降序排列 Arrays.sort(intvs,(a,b)->{ if(a[0]==b[0]){ returnb[1]-a[1]; } returna[0]-b[0]; }); //記錄合并區間的起點和終點 intleft=intvs[0][0]; intright=intvs[0][1]; intres=0; for(inti=1;i=intv[1]){ res++; } //情況二，找到相交區間，合并 if(right>=intv[0]&&right<=?intv[1])?{ ????????????right?=?intv[1]; ????????} ????????//?情況三，完全不相交，更新起點和終點 ????????if?(right?

以上就是本題的解法代碼，起點升序排列，終點降序排列的目的是防止如下情況：

對于這兩個起點相同的區間，我們需要保證長的那個區間在上面（按照終點降序），這樣才會被判定為覆蓋，否則會被錯誤地判定為相交，少算一個覆蓋區間。

區間合并問題

力扣第 56 題就是一道相關問題，題目很好理解：

title

我們解決區間問題的一般思路是先排序，然后觀察規律。

一個區間可以表示為[start, end]，前文聊的區間調度問題，需要按end排序，以便滿足貪心選擇性質。而對于區間合并問題，其實按end和start排序都可以，不過為了清晰起見，我們選擇按start排序。

顯然，對于幾個相交區間合并后的結果區間x，x.start一定是這些相交區間中start最小的，x.end一定是這些相交區間中end最大的。

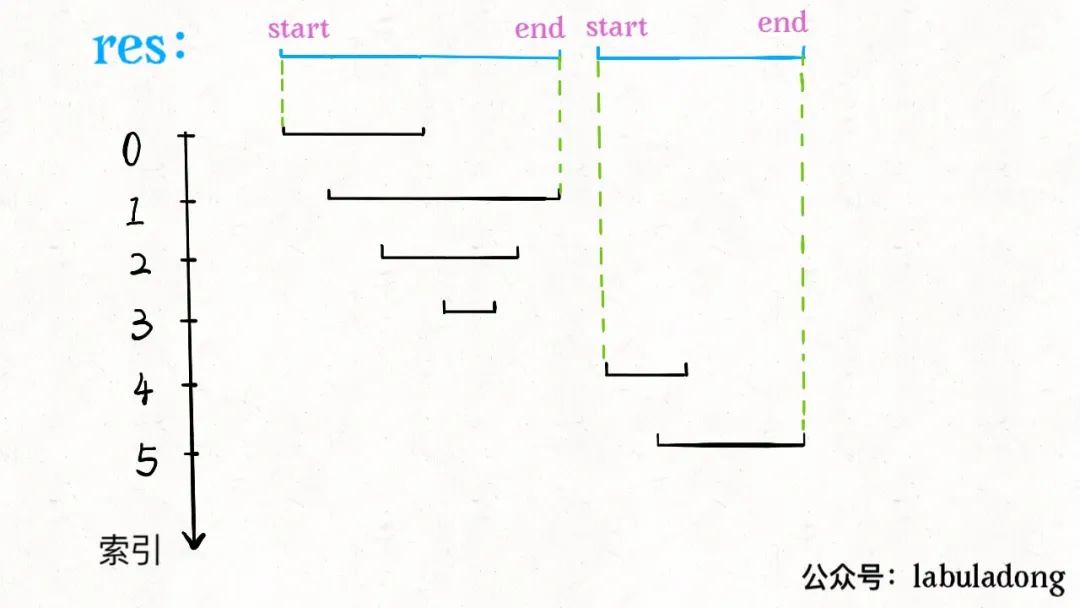
由于已經排了序，x.start很好確定，求x.end也很容易，可以類比在數組中找最大值的過程：

intmax_ele=arr[0]; for(inti=1;i

然后就可以寫出完整代碼

#intervals形如[[1,3],[2,6]...] defmerge(intervals): ifnotintervals:return[] #按區間的start升序排列 intervals.sort(key=lambdaintv:intv[0]) res=[] res.append(intervals[0]) foriinrange(1,len(intervals)): curr=intervals[i] #res中最后一個元素的引用 last=res[-1] ifcurr[0]<=?last[1]: ????????????#?找到最大的?end ????????????last[1]?=?max(last[1],?curr[1]) ????????else: ????????????#?處理下一個待合并區間 ????????????res.append(curr) ????return?res

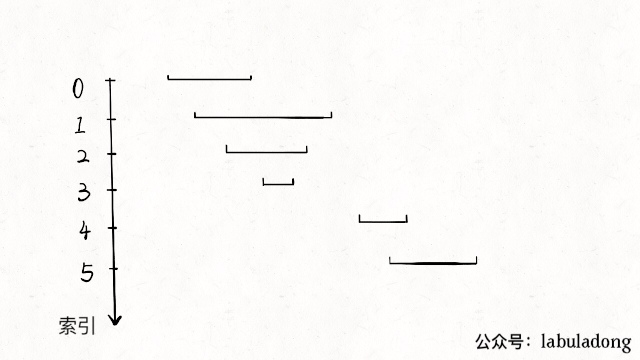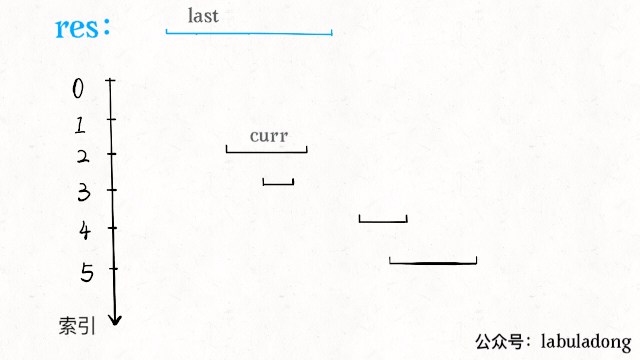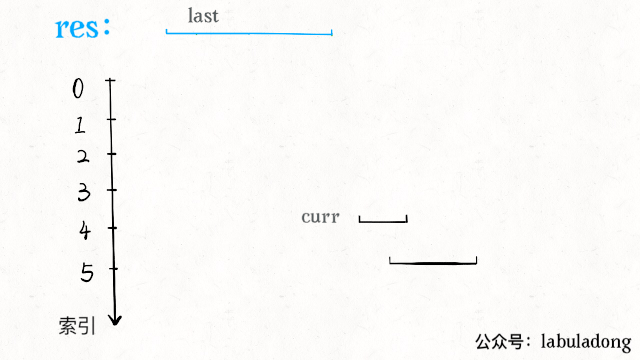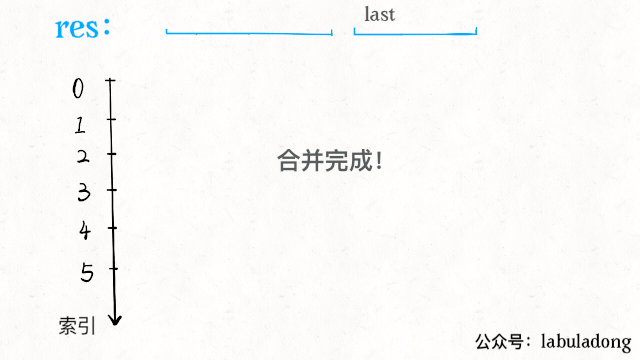
區間交集問題

先看下題目，力扣第 986 題就是這個問題：

title

題目很好理解，就是讓你找交集，注意區間都是閉區間。

解決區間問題的思路一般是先排序，以便操作，不過題目說已經排好序了，那么可以用兩個索引指針在A和B中游走，把交集找出來，代碼大概是這樣的：

#A,B形如[[0,2],[5,10]...] defintervalIntersection(A,B): i,j=0,0 res=[] whilei

不難，我們先老老實實分析一下各種情況。

首先，對于兩個區間，我們用[a1,a2]和[b1,b2]表示在A和B中的兩個區間，那么什么情況下這兩個區間沒有交集呢：

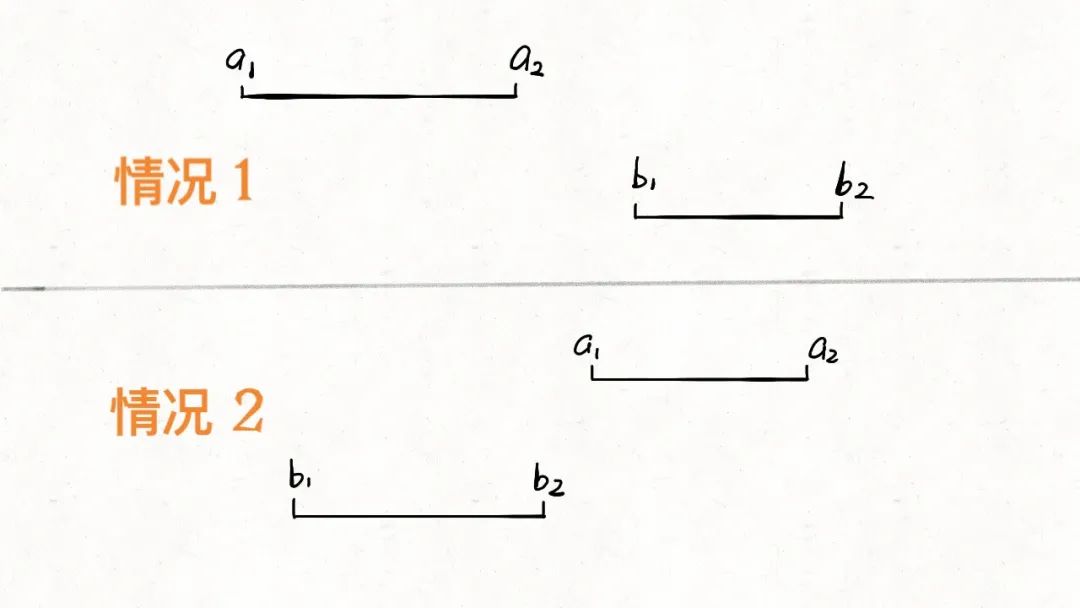
只有這兩種情況，寫成代碼的條件判斷就是這樣：

ifb2

那么，什么情況下，兩個區間存在交集呢？根據命題的否定，上面邏輯的否命題就是存在交集的條件：

#不等號取反，or也要變成and ifb2>=a1anda2>=b1: [a1,a2]和[b1,b2]存在交集

接下來，兩個區間存在交集的情況有哪些呢？窮舉出來：

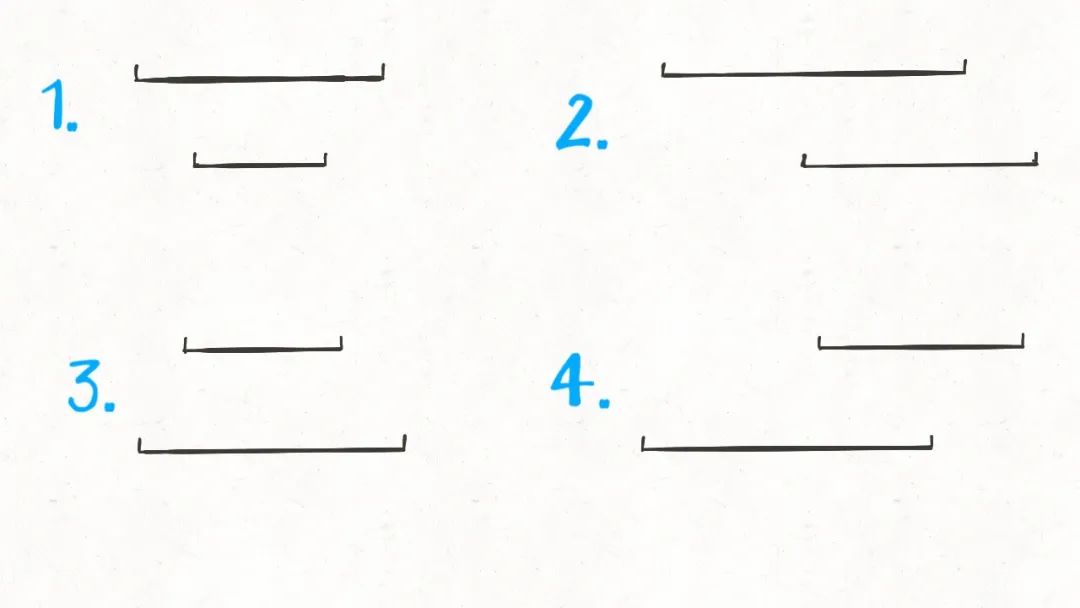
這很簡單吧，就這四種情況而已。那么接下來思考，這幾種情況下，交集是否有什么共同點呢？

我們驚奇地發現，交集區間是有規律的！如果交集區間是[c1,c2]，那么c1=max(a1,b1)，c2=min(a2,b2)！這一點就是尋找交集的核心，我們把代碼更進一步：

whilei=a1anda2>=b1: res.append([max(a1,b1),min(a2,b2)]) #...

最后一步，我們的指針i和j肯定要前進（遞增）的，什么時候應該前進呢？

結合動畫示例就很好理解了，是否前進，只取決于a2和b2的大小關系：

whilei

以此思路寫出代碼：

#A,B形如[[0,2],[5,10]...] defintervalIntersection(A,B): i,j=0,0#雙指針 res=[] whilei=a1anda2>=b1: #計算出交集，加入res res.append([max(a1,b1),min(a2,b2)]) #指針前進 ifb2

總結一下，區間類問題看起來都比較復雜，情況很多難以處理，但實際上通過觀察各種不同情況之間的共性可以發現規律，用簡潔的代碼就能處理。

責任編輯：xj

原文標題：一文秒殺所有區間相關問題

文章出處：【微信公眾號：算法與數據結構】歡迎添加關注！文章轉載請注明出處。