在了解弗來明左手定則前,更應該佩服一下羅倫茲力的發現,羅倫茲力定義了電能與磁能中力量產生的規則及原因。在電力學,羅倫茲力(Lorentz force)是運動于電磁場的帶電粒子所感受到的作用力,羅倫茲力是因荷蘭物理學者亨德里克·羅倫茲而命名

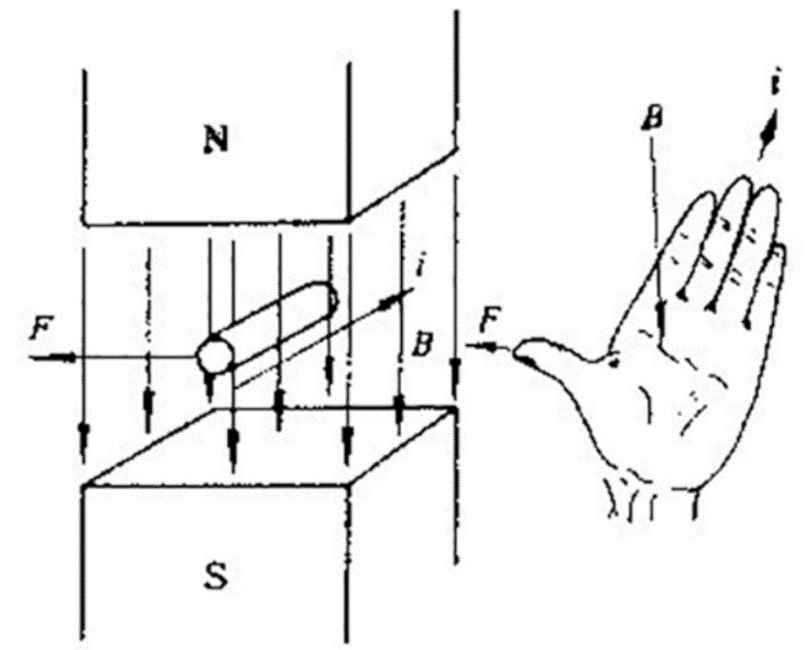
而弗來明左手定則只是用來說明電能、磁能及力量間的作用方向,它們之間呈現90度的正交角;補足了羅倫茲力所欠缺的一環。由向量的基本概念來看,完整地描述一個力量的作用,需要有力量大小的信息,同時亦需具備有方向信息,才是一個明確的作用力,因此羅倫茲力及弗來明左手定則幫助我們理解了電機中力量的表示。

將電機中的力量表示為數學式如下:

可發覺到其中有個Sin(δ)的式子,它就是用來定義電能與磁能是否90度正交的數學式。弗來明左手定則告訴我們,電機中的電能、磁能及力量間都是呈現90度正交角的交互作用,而一但電能與磁場不是90度時,則它們之間的關系就是正弦波Sin(δ)。
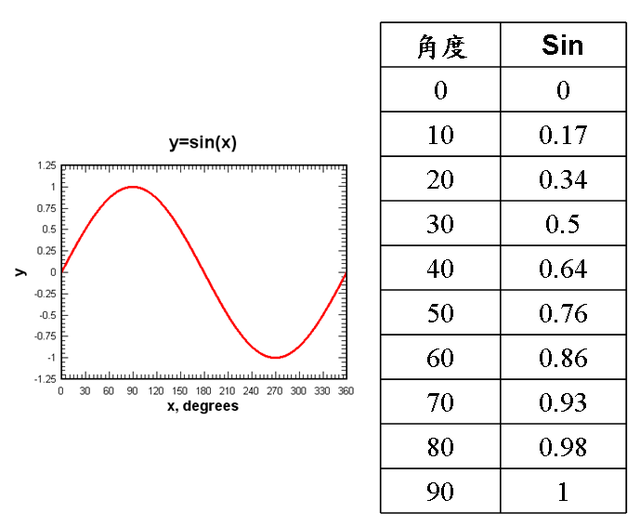
這正弦波關系也告訴我們另一件是,非90度的正交電機也會受力作用,但力度不是最大。 我們要先深究一下為什么90度正交角在電機中是個怎樣的位置,要知道電機中的角度表示,其實是采用電氣角,而非我們熟知的機械角,它們之間的換算公式如下:

其中Θe為電氣角度,Nm為磁場極數,Θm為機械角度。它們之間主要差了一個極性的倍數關系的,也就是1組NS極就是360度。其基本規格就可以用地球做完參考,我們知道地球有南北兩極且具有磁性,分別為N極與S極,而且地球是一個圓,因此有360度的角度。但在電機中,可能不僅僅有一組NS極,因此每一組的NS極,都要代表360度才符合我們印象中的地球狀態;電機中特別把這360度取名為電氣角度,而非我們日常看到的一個圓的360度機械角。
由此可知,其實一個磁極包括了180度的電氣角,而弗來明左手定則告知我們最大的作用力是在90度角的正交處,其實也就是磁極的正中心,本來就是磁力最強最集中之處,為了得到最大的力作用,選在磁場最強之處作用,當然得到最大力量,這點是十分合情合理的。而且這還進一步的定義了電機控制中常用的dq軸表示方式,即為磁力最強與最弱之處。
結論電機的驅動若想達到最大轉矩輸出,則要抓準Sin(δ)最大之處,也就是90度的正交角來驅動電機。實際上這點還是很難抓得準,所以Sin(δ)的正弦波關系,其實誤差到20度以內都還不會偏差太大,Sin(70)也有0.93%的效果,但要注意,電機極數越多時,電氣角對應的機械角的范圍越小,則在機械角上差的1~2度,電氣角度可能就超過20度,那影響就越來越大了。 感測器的解析度不足,或是安裝的公差太大時,對電機驅動來說,就變成了一場災難了。若是了解此一情況,還可以用軟件來修正,若是不知道,恐怕做出來的電機就永遠輸人一截。
責任編輯人:CC
-
電機驅動
+關注
關注
60文章
1215瀏覽量
86723
原文標題:如何用弗來明左手定則(Fleming's Left Hand Rule)來進行電機驅動
文章出處:【微信號:wwygzxcpj,微信公眾號:電機技術及應用】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
無刷電機霍爾傳感器位置及電機旋向確認方法研究
有刷電機/無刷電機基本原理與設計資料分享
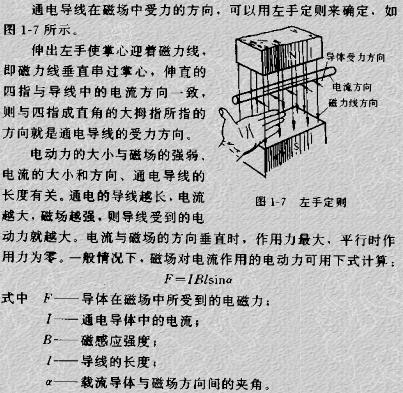
什么是左手定則?
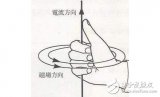
楞次定律右手定則_右手定則應用_右手定則用法
伺服電機結構原理分析
如何分清左、右手定則和右手螺旋定則
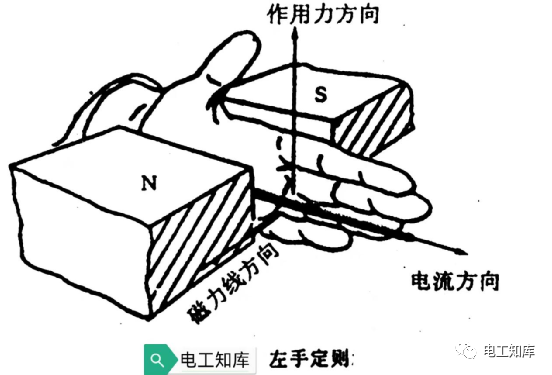




 弗來明左手定則進行電機驅動的方法
弗來明左手定則進行電機驅動的方法










評論