本文的目標(biāo)是提供方法和指導(dǎo),以便在必須將模數(shù)轉(zhuǎn)換器 (ADC) 放置在數(shù)字通信接收器中時指定模數(shù)轉(zhuǎn)換器 (ADC)。在這種情況下,由于所涉及信號的性質(zhì),規(guī)范過程需要特別注意。信道噪聲和干擾的存在使任務(wù)復(fù)雜化。在本文中,考慮了最重要的問題,例如噪聲預(yù)算、線性度要求和時序抖動以及相位噪聲。為了簡化讀者的理解過程,每個給定的規(guī)范都提供了數(shù)值示例。
噪音預(yù)算
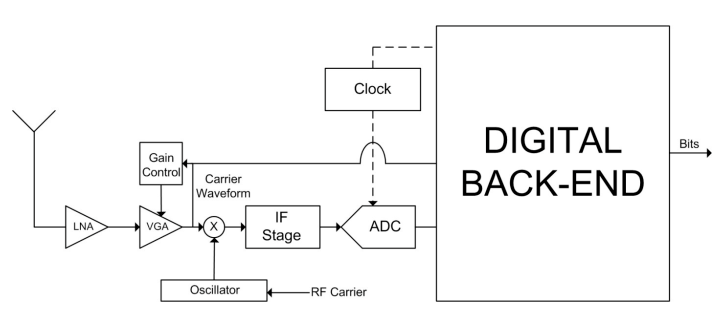
現(xiàn)代數(shù)字接收器必須執(zhí)行濾波、頻譜轉(zhuǎn)換和模數(shù)轉(zhuǎn)換等第一層任務(wù)。接收器還必須執(zhí)行一些估計接收信號的未知參數(shù)(例如幅度、頻率和定時對齊)所需的第二層任務(wù)。圖 1 顯示了典型數(shù)字接收機中第一層和第二層處理的框圖。模數(shù)轉(zhuǎn)換器對模擬中頻 (IF) 濾波器的輸出進(jìn)行采樣,該濾波器由數(shù)字下變頻器 (DDC) 下變頻到基帶。然后,基帶信號由抽取濾波器向下采樣,最后在匹配濾波器中進(jìn)行處理,以最大化呈現(xiàn)給檢測器的樣本的信噪比 (SNR)。該接收器的數(shù)字信號處理 (DSP) 部分包括載波對齊、定時恢復(fù)、信道均衡、自動增益控制、SNR 估計、信號檢測和干擾抑制模塊。由于接收器包含模擬硬件組件,它還包含許多第三層 DSP 模塊,以抑制由不完美模擬模塊形成的不希望有的偽像。
通常通過查看輸出端的誤碼率 (BER) 來考慮此類接收器的性能。BER 取決于輸入信號的 SNR。疊加在信號上的噪聲功率有兩個主要來源:信道和硬件設(shè)備。
ADC 是接收器的關(guān)鍵組件之一。它對模擬輸入信號進(jìn)行采樣,并將采樣傳送到接收器的基于 DSP 的部分,該部分處理諸如基帶移位、解調(diào)和信道均衡等任務(wù)。
接收信號時,由于信道引起的衰減,其信噪比(SNR)很低;通常它接近背景噪聲設(shè)置的限制。接收器前端(包括 ADC)的目標(biāo)是捕獲這個微弱信號并將其傳遞到接收器的數(shù)字部分,從而增加最小的退化(實現(xiàn)損失)。然而,由于某些降級是不可避免的,系統(tǒng)設(shè)計人員創(chuàng)建了一個系統(tǒng)陣容,其中為接收器的每個模塊分配了一定的噪聲預(yù)算。設(shè)計人員知道硬件設(shè)備可以添加到輸入信號的最大噪聲量,并根據(jù)輸入頻譜的特性和技術(shù)限制,決定如何在數(shù)字接收器中運行的不同處理模塊之間分配噪聲。
請注意,輸入信號最容易受到接收器前端的附加噪聲的影響,并且隨著放大而變得不那么敏感。出于這個原因,大部分接收器噪聲預(yù)算分配給前端模塊,例如低噪聲放大器 (LNA),而后端模塊(例如 ADC)或后面的數(shù)字模塊通常會收到較小的噪聲分配。
例如,假設(shè)輸入信號的 SNR 為 14dB,接收器所需的最小 SNR 為 12dB。然后系統(tǒng)可以將信號最大降低 2dB,這必須在不同的塊之間進(jìn)行拆分。假設(shè)已將 ADC 的噪聲分配選擇為最大 0.2dB(這意味著 ADC 可使 SNR 降低 0.2dB,而接收器的所有其他設(shè)備可使信號降低剩余的 1.8dB),則 SNR ADC 必須是

其中 SNRin 是接收信號的信噪比。
請注意,分配給 ADC 的總 SNR(以 dB 為單位)是其所有損傷
(噪聲、諧波失真和時鐘相位噪聲)的組合。設(shè)計人員決定
在這三者之間平均分配ADC分配,使各自的規(guī)格
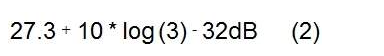
ADC 信噪比應(yīng)針對單個正弦波指定,該正弦波的幅度與器件的滿量程相匹配,該正弦波受整個奈奎斯特帶寬上的 ADC 熱噪聲和量化噪聲影響。在我們從未收到純正弦波的通信場景中,我們調(diào)制了攜帶我們想要傳輸?shù)男畔⒌恼也āR虼耍邮招盘柕念l譜與正弦波的頻譜非常不同。我們的目標(biāo)是了解指定帶限信號頻譜的 ADC SNR 分配與滿量程正弦波的 ADC SNR 之間的關(guān)系,以及我們?nèi)绾螐牡谝粋€實現(xiàn)第二個。
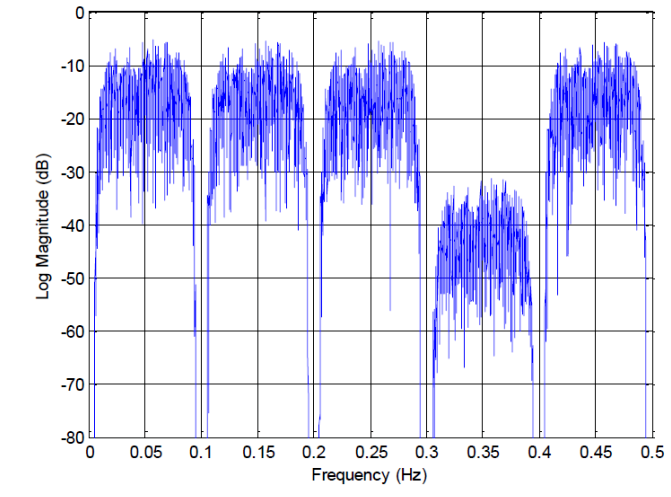
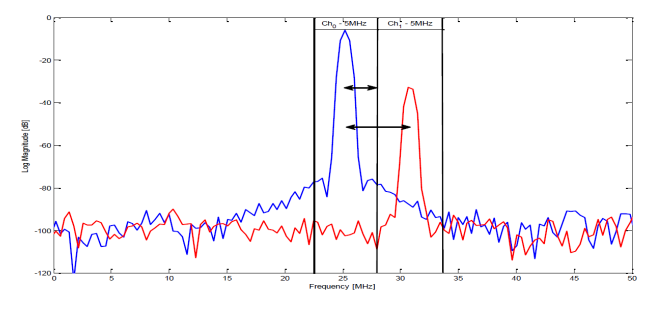
在下文中,我們考慮 ADC 輸入信號的典型最壞情況,該信號由四個等幅限帶通道和一個弱限帶通道組成,這是我們想要檢測的通道。這種情況的示例如圖 3 所示。強通道的功率為 ADC 的動態(tài)范圍設(shè)置了上限,而來自不同來源的噪聲和失真將其限制在下限。
為了計算 ADC SNR 分配,我們需要知道:
- ADC 輸入通道的相對功率
- ADC 輸入信號的峰均比 (PAR)
- 所需通道的帶寬 (bw)
- ADC 采樣率 (fs)
- ADC 輸入信號的復(fù)合(總)功率
ADC 是一個硬限制器。如果輸入信號電平在正側(cè)或負(fù)側(cè)超過 ADC 代碼范圍,則 ADC 輸出代碼將飽和至其最大值或最小值。一旦發(fā)生這種削波,輸出信號值就會產(chǎn)生很大的誤差,對信號 SNR 產(chǎn)生重大影響。確保輸入信號電平正確很重要,以免削波發(fā)生太頻繁。為了避免削波,用戶需要知道輸入信號的 PAR。該數(shù)字用作增益控制環(huán)路中的回退,用于監(jiān)控平均信號電平。在大多數(shù)情況下,為了確保輸入信號電平適合 ADC,在 ADC 之前將一個或多個可變增益放大器嵌入到接收器中。
在正弦波情況下,為指定 ADC 要做的第一件事是將 ADC 滿量程與接收信號電平進(jìn)行比較。請記住,我們假設(shè)輸入信號由五個等帶寬 (bw=5MHz) 通道組成;其中四個具有高功率電平,而所需通道的功率電平比其他通道低 25dB。我們還假設(shè)該信號的 PAR 為 12dB,而根據(jù)之前的計算(參見公式(2)),弱通道的 ADC SNR 分配為 32dB,其采樣率為 fs=100MHz。
第一步是將弱通道的幅度電平與 ADC 滿量程相關(guān)聯(lián)。推理是這樣進(jìn)行的:信號合成功率在ADC滿量程(PAR)以下12dB,每個強通道的功率在(10log(4)=6)以下6dB,而弱通道的功率在25dB以下那。綜上所述,弱電源的功率比ADC滿量程(12+6+25)低43dB。
在這一點上,我們需要計算過采樣增益,它考慮到在單個正弦波的情況下需要考慮散布在整個奈奎斯特區(qū)的白噪聲,而在實際信號情況下只需要考慮噪聲下降信號帶寬會降低其 SNR。這是真的,因為我們假設(shè)在數(shù)字域中,在 ADC 之后,有一個濾波器可以去除信號帶寬之外的噪聲。
可以使用以下公式計算過采樣增益:
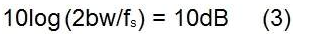
通過了解 ADC SNR 分配 (32dB)、相對于滿量程的弱信號幅度 (- ( – 43dB))、過采樣增益 (- 10dB) 和正弦波的 PAR 調(diào)整因子 (- 3dB) 我們可以計算滿量程正弦波的ADC SNR:(32+43-10-3)dB=62dB。
通常 RF 設(shè)計人員使用噪聲系數(shù) (NF) 而不是 SNR,因此將剛剛計算的信噪比與噪聲系數(shù)相關(guān)聯(lián)很重要。噪聲系數(shù)定義為 ADC 的總有效輸入噪聲功率與僅由源阻抗引起的噪聲功率量之比,以 dB 表示(見公式 (4))。
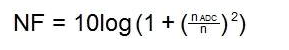
其中 nADC 是 ADC 噪聲,可使用公式 (5) 計算
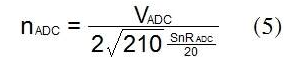
其中 VADC 是差分 ADC 滿量程,SNRADC 是單個正弦波的 ADC 噪聲分配,其峰峰值幅度恰好填充 ADC 輸入范圍。SNR ADC 的值通常顯示在各種輸入頻率的數(shù)據(jù)表上,那么我們必須確保使用與感興趣的 IF 輸入頻率相對應(yīng)的值。此外,我們必須確保基波信號的諧波不包含在 SNR 數(shù)中。等式(4)中的參數(shù) n 是源阻抗本身的噪聲
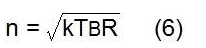
其中 k 是玻爾茲曼常數(shù),T 是以開爾文表示的溫度,B=fs/2,R 是阻抗。
請注意,公式 (4) 假設(shè) ADC 的輸入帶寬限制為 fs/2,濾波器的噪聲帶寬等于 fs/2。當(dāng)然,可以進(jìn)一步對輸入信號進(jìn)行頻帶限制,從而導(dǎo)致過采樣和處理增益。
線性規(guī)格
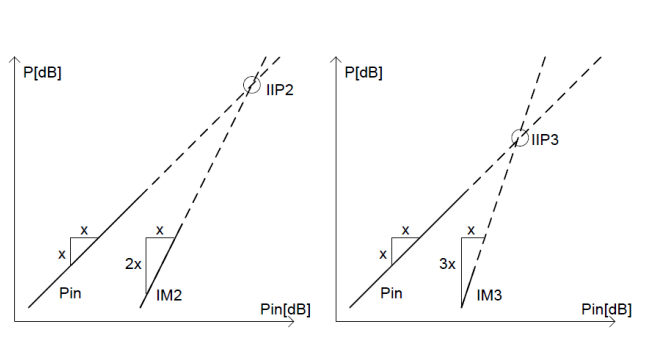
模擬電路通常具有許多不同的性能標(biāo)準(zhǔn),以便整體系統(tǒng)性能滿足所需的規(guī)格。對于模數(shù)轉(zhuǎn)換器,線性度是一個非常重要的問題,需要注意。它嚴(yán)重影響系統(tǒng)性能。眾所周知,如果將正弦波形應(yīng)用于線性時變系統(tǒng),輸出也將是相同頻率的正弦波形,但很可能具有不同的幅度和相位。然而,如果將相同的輸入信號應(yīng)用于非線性系統(tǒng),則輸出信號將具有輸入波形諧波處的頻率分量,包括基頻。最重要的無用諧波分量是二階和三階失真分量(通常稱為 IM2 和 IM3)。通常,ADC 線性度是使用總諧波失真 (THD) 或使用單個諧波的電平(例如 HD2 和 HD3)來指定的。ADC 設(shè)計人員可以通過單音正弦輸入信號測試來模擬或測量這些參數(shù)。雙音測試也常用,并給出 IM2 和 IM3 規(guī)格。然而,現(xiàn)實世界的信號與正弦波不同;他們的PAR要高得多,因此這些測試并不準(zhǔn)確。
與 IM2 和 IM3 不同,RF 設(shè)計人員更喜歡考慮二階交調(diào)點 (IIP2) 和三階交調(diào)點 (IIP3),它們與 IM2 和 IM3 的關(guān)系如圖 3 所示。最壞的情況通常是接收弱信號和高功率信號。在這種情況下,我們可以通過用兩個正弦波對強信號進(jìn)行建模來設(shè)置雙音測試,同時互調(diào)產(chǎn)品落在弱有用信號通道上;這里的基本問題是正弦波的峰值是否應(yīng)該與調(diào)制信號的峰值匹配,或者它是否應(yīng)該與 rms 匹配。這兩個選項都不是正確的,因為第一個選項過度指定了 ADC 的線性要求,而第二個選項給出的數(shù)字不足以滿足實際調(diào)制信號的要求。大多數(shù)情況下,模擬是解決問題的最佳方法。有時還會執(zhí)行噪聲功率比 (NPR) 測試或缺失音調(diào)功率比 (MTPR) 測試,它們更接近于許多現(xiàn)實世界的使用場景。然而,NPR 測試無法使用常用的正弦信號源執(zhí)行,因此通常會避免使用。在 [2] 中可以找到有關(guān)此主題的更多詳細(xì)信息以及實際示例。
時鐘相位噪聲和時序抖動
采樣時鐘邊沿與理想位置的位移稱為時鐘(或定時)抖動。時鐘抖動可以是隨機的,源于時鐘生成電路和時鐘分配網(wǎng)絡(luò)的噪聲,也可以是系統(tǒng)性的,因為另一個信號耦合到時鐘。但是,它沒有描述時鐘誤差的頻譜分布。出于這個原因,有時最好使用相位噪聲來代替。
相位噪聲可以定義為頻譜圖或載波周圍特定頻率范圍內(nèi)噪聲功率譜密度的積分。通常使用鎖相環(huán) (PLL) 生成 ADC 采樣時鐘。PLL 的特征相位噪聲曲線在載波周圍有一個升高的本底噪聲區(qū)域,其中大部分噪聲功率集中。在許多情況下,為接近相位噪聲和該區(qū)域外的噪聲制定單獨的規(guī)范是有意義的。相位噪聲功率或功率譜密度通常表示為相對于以 dBc 為單位的載波功率。這樣,相位噪聲的單位可以被認(rèn)為是弧度,因此取決于時鐘周期。相位噪聲總是在某個載波頻率下指定,通常在 PLL 的輸出頻率上,
分頻時鐘的相位噪聲為:
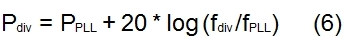
抖動以秒為單位測量,時間是絕對的,當(dāng)時鐘頻率被分頻時,它的抖動不會改變。請注意,時鐘抖動和相位噪聲是描述相同現(xiàn)象的兩種不同方式。
集成相位噪聲被指定為單邊帶 (SSB) 或雙邊帶 (DSB)。通常相位噪聲關(guān)于載波是對稱的,因此

在下圖中,我們給出了當(dāng)輸入信號是一個以 20MHz 為中心的純正弦波并且考慮的噪聲源僅為相位噪聲時的 ADC SNR 數(shù)值示例。PLL 的集成單邊帶相位噪聲在 1GHz 時設(shè)置為 -38dBc。ADC 采樣時鐘 (100MHz) 是從該信號除以 10 生成的。在這種情況下,時鐘的相位噪聲輪廓出現(xiàn)在采樣信號周圍,其幅度為 (20*log(fsig/fclk))。當(dāng)存在其他噪聲源時,該因素必須從總 ADC SNR 進(jìn)行調(diào)整。通過將公式 (7) 與我們?yōu)閿?shù)值示例選擇的數(shù)字應(yīng)用,我們發(fā)現(xiàn) ADC 時鐘頻率下的 DSB 相位噪聲為

相位噪聲和時序抖動的最終結(jié)果應(yīng)該是一樣的。請注意,當(dāng)我們將正弦波視為輸入信號時,噪聲功率被視為分布在整個奈奎斯特頻帶上。在實際情況下,接收信號的帶寬是有限的,只需要考慮分布在該頻段上的噪聲部分。如果噪聲在頻譜上是白色的(這通常是抖動的假設(shè)),則可以使用過采樣率(在上一節(jié)中計算)來獲得 SNR。當(dāng)噪聲不能被視為白噪聲(PLL 的接近相位噪聲)時,不能使用此方法。這種情況通常發(fā)生在所需信號靠近強干擾源或介于更強干擾信號之間時。
然而,正弦波在設(shè)計過程中仍然非常重要。事實上,如果我們在 ADC 的輸入端有兩個信號,一個比另一個弱得多,寬度均為 5MHz,間隔為 5MHz,強通道的中心頻率為 25MHz。弱通道的 SNR 要求為 32dB,強通道的幅度比弱通道高 25dB。驅(qū)動時鐘的 PLL 的輸出頻率為 1GHz。在這種情況下,通過在其頻率范圍的中心用正弦波對更強的信道進(jìn)行建模,如圖 4 所示,我們實現(xiàn)了近似的相位噪聲規(guī)范,這導(dǎo)致了以下要求:從 2.5MHz 積分的 SSB 相位噪聲到 7.5MHz 在 25MHz 時必須小于 57dB (25+32)。相同的計算,在 1GHz PLL 頻率下指定,
對于多個強干擾信道之間的弱有用信號支架的情況,我們可以考慮以下數(shù)值示例:干擾信道寬5MHz,弱信道以15MHz為中心,其他在20、25、30和35MHz。強通道的幅度比弱通道高 25dB。ADC 采樣率為 100MHz,弱通道所需的 SNR 為 32dB。相位噪聲假定為白色。在這種情況下,我們使用以信道中心頻率的平均值為中心的單個正弦波對信道進(jìn)行建模,其功率等于四個信道的總功率。再次計算這個虛信號的抖動要求,我們得到:
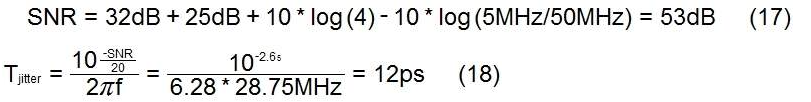
然而,只有通過系統(tǒng)仿真才能獲得更準(zhǔn)確的抖動規(guī)范。
參考
[1] David A. Johns、Ken Martin,“模擬集成電路設(shè)計”,John Wiley & Sons, Inc. 紐約。
[2] Mikko Waltari,“如何為數(shù)字通信接收器指定 ADC”,可在http://www.iqanalog.com/compan...
[3] Mikko Waltari 和 Kari Halonen,低壓和高壓電路技術(shù)- 速度 A/D 轉(zhuǎn)換器,Kluwer Academic Publishers,2002 年。
編輯:hfy
-
接收器
+關(guān)注
關(guān)注
15文章
2571瀏覽量
73941 -
adc
+關(guān)注
關(guān)注
99文章
6709瀏覽量
549229 -
模數(shù)轉(zhuǎn)換器
+關(guān)注
關(guān)注
26文章
3359瀏覽量
128272 -
數(shù)字通信
+關(guān)注
關(guān)注
1文章
147瀏覽量
22896
發(fā)布評論請先 登錄
藍(lán)牙接收器SRRC認(rèn)證流程解析

USB接收器的安裝和使用
應(yīng)用在數(shù)字衛(wèi)星接收器領(lǐng)域的射頻放大芯片-WT20-1809

DC/DC 轉(zhuǎn)換器輸出電壓調(diào)整的方法,包括數(shù)字通信接口、數(shù)字輸入和模擬輸入三種方式
數(shù)字通信分析儀的技術(shù)原理和應(yīng)用
ADC噪聲系數(shù)對射頻接收器的影響

ISO1228 ISO1228DFBEVM 8 通道隔離式數(shù)字輸入接收器評估模塊





















評論