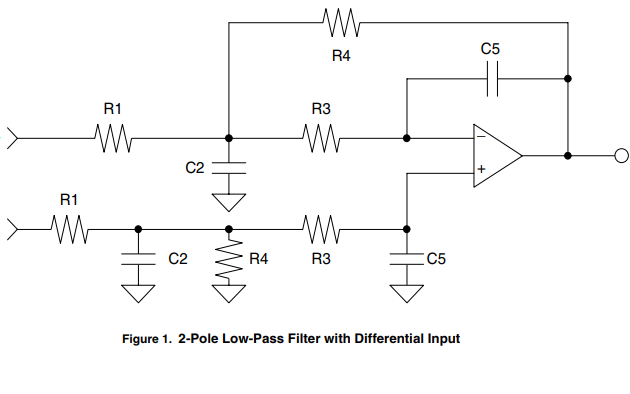
當今的許多數字 DAC 都需要一個具有差分輸入的電路，它將消除共模誤差、減少由 delta-sigma 調制器產生的帶外噪聲并產生單端輸出。圖 1 中的電路包括一個差分輸入和一個兩極模擬濾波器來實現這些設計要求。本應用筆記概述了選擇組件值所需的設計步驟。

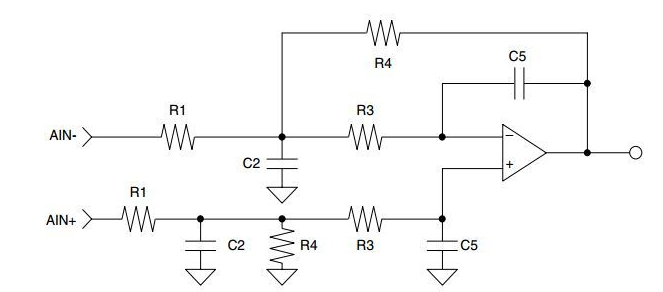
多反饋低通濾波器

請注意圖 1 和圖 2 中所示的多反饋低通濾波器之間的相似之處。使用多反饋低通濾波器的設計方程可以輕松設計具有差分輸入的 2 極點低通濾波器。另外，請注意圖 1 和圖 3 之間的相似之處。差分輸入功能是通過簡單地復制濾波器設計中生成的元件值來實現的。

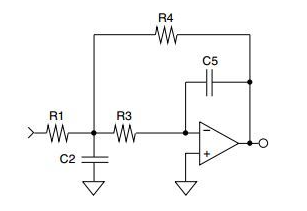
多反饋低通濾波器

設計步驟

步驟 1：確定所需的通帶增益 [tex]H _{0}[/tex]。電路參數要求[tex]H_{0}[/tex]的幅度大于或等于1。由于反相運算放大器配置，[tex]H _{0}[/tex] 也為負。

步驟 2：確定最小輸入阻抗。

步驟 3：為最終設計選擇所需的濾波器類型，Butterworth、Bessel 等，以及其他角頻率 [tex]F _{C[/tex]。濾波器響應和轉角頻率決定了通帶相位和幅度響應。濾波器類型決定了極點位置，因此決定了 alpha 和 beta。表 1 列出了幾種濾波器類型的歸一化極點位置。

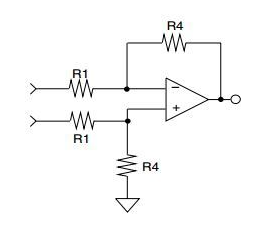
差分輸入電路

步驟 4：為 C5 和 C2 選擇方便的值。注意在第 5 步中，必須選擇 [tex]K[/tex] 和 [tex]H _{0}[/tex] 使得 [tex]sqrt{zeta ^{2}-K(1-H _{0 })}[/tex] 是真實的。

第五步：給定 [tex]F _{C}[/tex], [tex]H _{0}[/tex], [tex]C _{2}[/tex], [tex]C _{5 }[/tex]，alpha 和 beta，使用以下公式計算 R1、R2 和 R3：

[tex]zeta = frac{alpha }{sqrt {alpha ^{2}+beta ^{2}}}[/tex]

[tex]omega _{0} = 2pi F _{c} {sqrt {alpha ^{2}+beta ^{2}}}[/tex]

[tex]K=frac{C _{5}}{C _{2}}[/tex]

[tex]R _{1}=frac{R _{4}}{(-H _{0})}[/tex]

[tex]R _{3}=frac{1}{omega _{0}C _{2}[zeta pm {sqrt{zeta ^{2}-K(1- H _{0})}}]} [/特克斯]

[tex]R _{4} = frac{zeta pm {sqrt {zeta _{2}-K(1-H _{0})}}}{omega _{0}cdot C _{5}}[/特克斯]

步驟 6：查看電阻器和電容器值。希望保持足夠大的電容器值以最小化雜散電容的影響。可能需要調整在步驟 4 中選擇的電容器值以達到此要求。還要驗證 R1 是否大于所需的最小輸入阻抗。

第七步：第五步計算出來的電阻值一般都不是標準值。選擇最接近計算值的標準值。這不會對濾波器特性造成大的變化，因為金屬膜電阻器可以以大約 2.5% 的增量提供，這允許選擇接近計算值的元件。但是，建議使用選定的值，使用步驟 5 中的公式計算實際濾波器參數。

步驟 8：從單端電路到差分電路的轉換需要復制同相輸入中 R1、C2、R3、R4 和 C5 的值，如圖 1 所示。

編輯：hfy