在本文中，我們描述了在 M 通道時間交錯模數轉換器 （TI-ADC） 的一般情況下，時序和增益失配對采樣信號的影響，并提出了一種適用于雙通道 TI- ADC 案例。

時序和增益失配的數字校正

作者：Elettra Venosa 博士，IQ-Analog，SDSU，Mikko Waltari 博士，IQ-Analog，

fred harris 博士，SDSU，Mike Kappes，IQ-Analog

時間交織 （TI） 是克服硬件技術強加的約束的最有效方法，這些約束通過降低實現成本和功耗來限制模數轉換器 （ADC） 的最大采樣頻率。低功耗、較低的實現成本、高采樣頻率和高分辨率是多用途基于 DSP 的通信接收器非常需要的特性。不幸的是，當以時間交錯方式使用 ADC 時，會引入通道之間的時序和增益不匹配。這些不匹配對這些系統的性能具有強烈的不利影響。在這份白皮書中，我們在 M 通道時間交錯模數轉換器 （TI-ADC） 的一般情況下描述了時序和增益失配對采樣信號的影響，并提出了適用于雙通道 TI-ADC 情況的解決方案。

所提出的解決方案非常通用并且與當前市場上存在的其他解決方案相比也是獨特的，因為它在應用中頻（IF）載波的子采樣時在通信場景中起作用。這種低速率采樣方法在通信接收器中越來越流行，因為它有望降低工作量和功耗。我們的解決方案完全在數字域中實施，在 TI-ADC 采樣時在后臺運行，并允許在不犧牲分辨率的情況下完全校正失配。所提出的解決方案非常通用并且與當前市場上存在的其他解決方案相比也是獨特的，因為它在應用中頻（IF）載波的子采樣時在通信場景中起作用。

這種低速率采樣方法在通信接收器中越來越流行，因為它有望降低工作量和功耗。我們的解決方案完全在數字域中實施，在 TI-ADC 采樣時在后臺運行，并允許在不犧牲分辨率的情況下完全校正失配。所提出的解決方案非常通用并且與當前市場上存在的其他解決方案相比也是獨特的，因為它在應用中頻（IF）載波的子采樣時在通信場景中起作用。這種低速率采樣方法在通信接收器中越來越流行，因為它有望降低工作量和功耗。

我們的解決方案完全在數字域中實施，在 TI-ADC 采樣時在后臺運行，并允許在不犧牲分辨率的情況下完全校正失配。這種低速率采樣方法在通信接收器中越來越流行，因為它有望降低工作量和功耗。我們的解決方案完全在數字域中實施，在 TI-ADC 采樣時在后臺運行，并允許在不犧牲分辨率的情況下完全校正失配。這種低速率采樣方法在通信接收器中越來越流行，因為它有望降低工作量和功耗。我們的解決方案完全在數字域中實施，在 TI-ADC 采樣時在后臺運行，并允許在不犧牲分辨率的情況下完全校正失配。

ADC 基礎

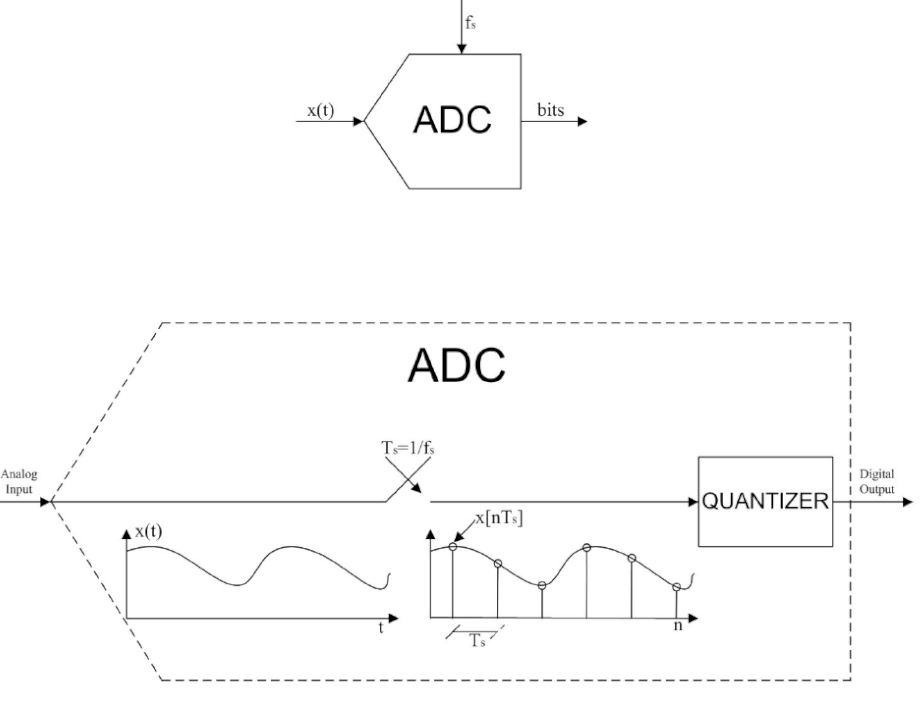
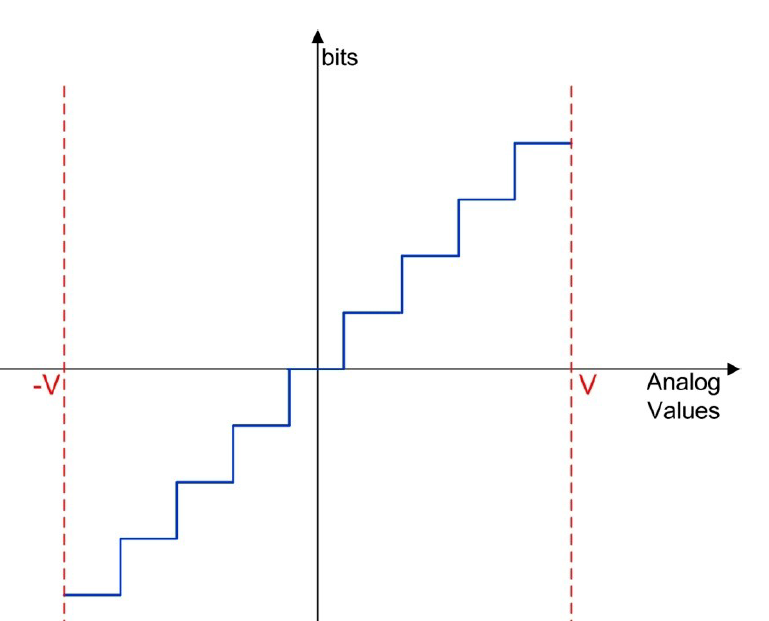
模數轉換器將模擬量（這是“現實世界”中大多數現象的特征）轉換為數字域，用于信息處理、計算、數據傳輸和控制系統。理想 ADC 的輸入和輸出之間的關系如圖 1 所示。模擬信號 x（t） 首先通過一個采樣器進行處理，該采樣器在固定的周期性、均勻分布、離散的時間瞬間取其值，并指定分辨率通過采樣頻率 fs=1/Ts。然后離散時間樣本被量化并編碼為位字。量化器通過應用圖 2 所示的傳遞函數將連續值轉換為固定的離散值。當設計需要時，稍微不同的曲線（圍繞零不對稱或具有非均勻分布的步長）可以描述量化過程。量化值隨后被編碼為數字 N 位字。

實際上，模擬信號的數字化遠非剛剛描述的理想過程。量化器實際上引入了錯誤，這是由于用 2N 個離散值的有限集表示模擬連續值的近似值。包含在某個固定間隔中的所有模擬信號值都與相同的離散輸出值相關聯（請看圖 2 中的曲線）。這種近似對量化器輸出值施加了不確定性，通常將其建模為零均值、不相關的噪聲，稱為量化噪聲。這種噪聲可以減少（例如通過增加位數），但永遠無法完全避免。請注意，在實踐中，由于 ADC 實現中的不準確和不匹配，

采樣過程中涉及的硬件設備（采樣器和時鐘發生器）的性質也會導致輸出采樣數據的精度損失。這種不精確性有兩個分量（隨機和確定性），可以通過時序抖動和時序偏移誤差很好地建模。這兩種現象完全不同，因此必須使用不同的模型來描述它們并使用不同的方法進行補償。特別是，雖然時序抖動具有隨機性并且可以相關或不相關（彩色時序抖動和白色時序抖動），但時序偏移是確定性延遲。當輸入信號的頻率較高時，相關的時序抖動以及時序偏移會產生更顯著的影響。通常，即使它們與整個采樣周期相比非常小，它們會產生破壞性影響，從而影響高精度應用。在高采樣頻率下，對精度的限制實際上變得更加嚴格。

我們的目標是在不影響 ADC 性能和實現成本的情況下提高轉換過程的采樣頻率。一個很好的解決方案是時間交錯架構。時間交錯 ADC 是一種通過使用多個較低采樣率 ADC 來提高系統整體采樣頻率的有效方法。

不幸的是，當兩個或多個模數轉換器時間交錯時，轉換過程會受到通道之間時序和增益不匹配的影響。當輸入信號具有帶通特性時，所有已知的用于校正這些失配的解決方案都是無效的，而帶通特性恰好是數字通信接收機最常見的情況。當前用于 TI-ADC 的識別和校正架構也無法解決所需信號頻譜副本不在第一奈奎斯特區域而是駐留在更高階奈奎??斯特區域中的問題。高階奈奎斯特區域上的帶通采樣通常用于通信場景中，其中所涉及的信號在頻域中具有稀疏特性。

在下一節中，我們將簡要解釋增益和時序失配對 TI-ADC 輸入信號的影響，然后我們將介紹我們的解決方案，用于識別和糾正雙通道 TI-ADC 情況下這些失配導致的偽影。

時間交錯架構

存在多種適用于高采樣率、高精度應用的 ADC 架構（分段、折疊、流水線、逐次逼近寄存器等）。在每種情況下，功率和速度之間都有明顯的權衡，這限制了架構可以服務的應用范圍。可以通過使用時間交錯多個 ADC 內核來消除這種折衷。

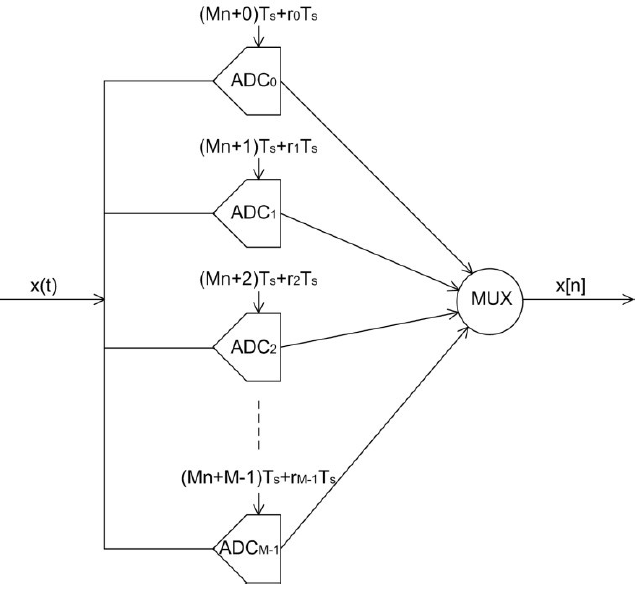
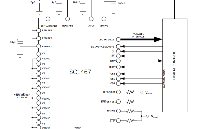
圖 3 顯示了 M 通道 TI-ADC 架構的框圖。在交錯方式中，兩個或多個 ADC 并行放置，它們的樣本由多路復用器進行時間交錯。系統的整體采樣頻率必須驗證 Nyquist 采樣定理，該定理指出

fs ≥ BW + Δf （1）

其中 BW 是信號帶寬，Δf 是抗混疊濾波器 ［1］ 所需的額外帶寬。但是，對于每個臂，不需要驗證奈奎斯特采樣標準，因此，每個 TI-ADC 通道以總采樣頻率 fs 的 1/M 對模擬信號進行采樣。每個采樣器的起始點（初始時間）延遲 mTs/M。這個時移變成頻域中的相移。在理想情況下，每個通道上的相移是這樣的，當來自每個通道的樣本被多路復用器交織時，不需要的混疊信號副本相消地相加在一起，而只有所需的副本相長相加在一起。

當兩個或多個模數轉換器進行時間交織時，轉換過程會受到通道之間的時序和增益不匹配的影響，這會破壞多路復用過程。

頻道不匹配

TI-ADC 有兩個主要問題來源：時序偏移 r0 和增益偏移 g0。時序偏移是 ADC 對輸入信號進行采樣的理想時刻與 ADC 對輸入信號進行采樣的實時時刻之間的差值。增益偏移是應用于輸入信號幅度的乘法增益。這些參數源于不可避免的制造工藝缺陷以及更系統的電路布局和寄生差異??。它們通常非常小，當 ADC 以獨立方式使用時，它們不會影響其性能。然而，它們在時間交錯架構中成為相當大的問題。這些問題是由時間交錯系統中使用的各個 ADC 之間的差異引起的，通常稱為通道失配錯誤。信道失配誤差引起失真。

在雙通道時間交錯架構中使用時，兩個 ADC 并行運行，其 2Ts 時間間隔采樣時鐘的時間偏移為 Ts。當多路復用正確時，系統的整體采樣頻率會加倍。在理想的雙通道 TI-ADC 中，由以半速率運行的單個 ADC 形成的混疊項被交錯過程消除。發生這種消除是因為時間偏移 ADC 的混疊頻譜分量與非時間偏移 ADC 的相同頻譜分量具有相反的相位。在沒有時間偏移和增益失配的情況下，它們的頻譜總和將消除不需要的混疊分量。

由于增益和定時相位不匹配，來自交錯時間序列副本的不需要的頻譜分量的總和不為零。實際上，兩個 ADC 的采樣時刻受到恒定延遲 ?tm 的影響，其中 m = 0， 1，這會導致其混疊頻譜出現不希望的頻率相關相位偏移，從而防止它們在輸出端被完美抵消時分復用器。增益失配導致 TI-ADC 系統輸出端頻譜分量的頻率獨立不完美消除。

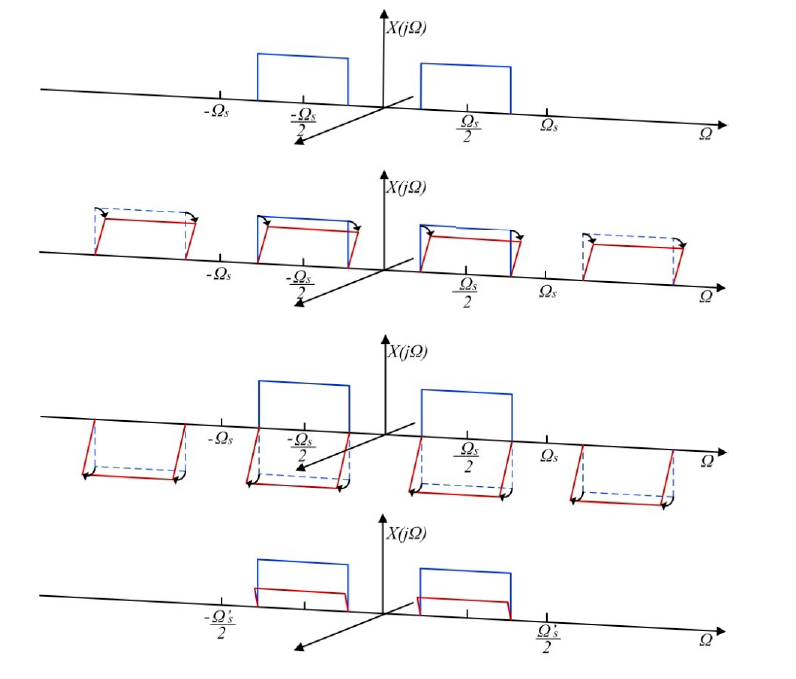
圖 4 說明了雙通道 TI-ADC 中增益和時間失配的影響，而圖 5 和圖 6 使用 Matlab 仿真顯示了時序和增益失配對雙通道 TI-ADC 輸出頻譜的影響。 理想的 TI-ADC 情況（如圖 5 所示）顯示，由于不存在失配，所以完全消除了混疊副本。圖 6 所示的實際情況顯示了時序和增益失配的影響，這會導致來自第二個奈奎斯特區的混疊信號副本的不完美消除，這些副本在所需頻譜上清晰可見。在這兩個圖中，我們都使用了正弦波的組合作為樣本頻譜，以便在所需頻譜上清楚地顯示源自失配的混疊副本。

不匹配識別和更正

我們的目標是糾正采樣數據域中時序和增益偏移的影響。為了做到這一點，我們必須首先估計它??們。估計方法分為兩類：

? 前景技術，也稱為非盲法，通過測量對探頭的 TI-ADC 輸出響應，注入已知的測試或探頭信號以估計失配。

? 背景技術，也稱為盲法，不需要有關輸入信號的信息（可能除了有關某些頻帶中信號活動的存在或不存在的一些知識）來估計失配。

第一種方法的缺點是正常的 TI-ADC 操作在探測期間暫停，但在第二種方法中，校準過程不會中斷正常的 TI-ADC 操作。

文獻中有許多論文在雙通道 TI-ADC ［2］、［4］ 中使用盲法或非盲法估計和校正方法。在 ［2］ 中，作者通過基于最小均方 （LMS） 算法的自適應方法估計時間失配。假設輸入信號頻譜是低通的并且略微過采樣。最后一個假設創建了一個僅包含不需要的別名分量的失配帶。通過這種技術實現的混疊與非混疊頻譜電平比的總體改進約為 26dB。［2］ 中提出的結構已在最近的一篇論文 ［3］ 中推廣到 M 通道 TI-ADC 的情況。在 ［4］ 中，作者提出了一種自適應濾波結構，該結構使用三個固定 FIR 濾波器和兩個自適應增益和延遲參數來執行校準。對輸入信號的假設與 ［2］ 中的相同，即它是一個略微過采樣的低通信號。這種結構實現了 《26dB 的改進。以上引用的論文中的所有估計和校正結構都是假設輸入信號具有低通特性而導出的。

我們提出的解決方案完全獨立于信號頻譜和所選的整體 TI-ADC 采樣頻率，因此它也適用于應用稀疏采樣（子采樣）的帶通信號。

圖 7 顯示了雙通道 TI-ADC 的框圖，后跟用于在數字域中運行的增益和時序失配的估計和補償結構。

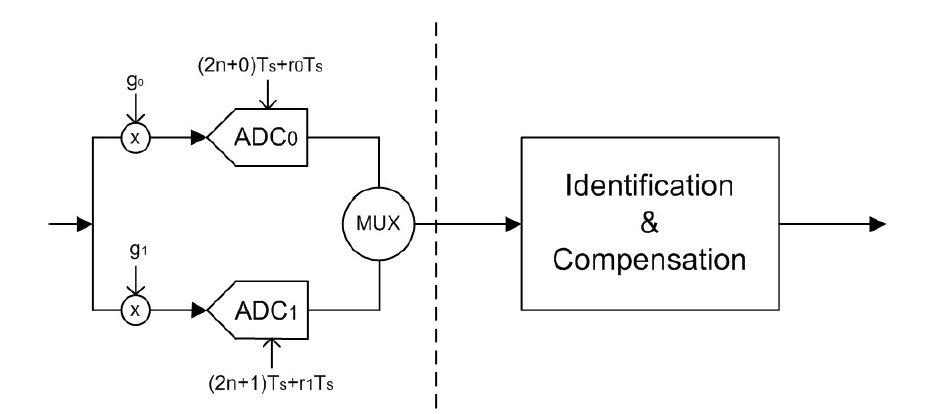
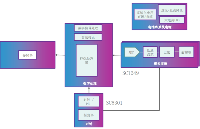
圖 8 詳細說明了識別和補償組件。該架構基于 ［2］ 和 ［3］ 中派生的結構。它基于這樣的假設，即時序偏移相對于整個采樣周期 Ts 較小，并且它們的平均值為零。我們將對這種結構進行一些重要的修改，以便在將低速率采樣應用于稀疏信號時糾正通道失配。

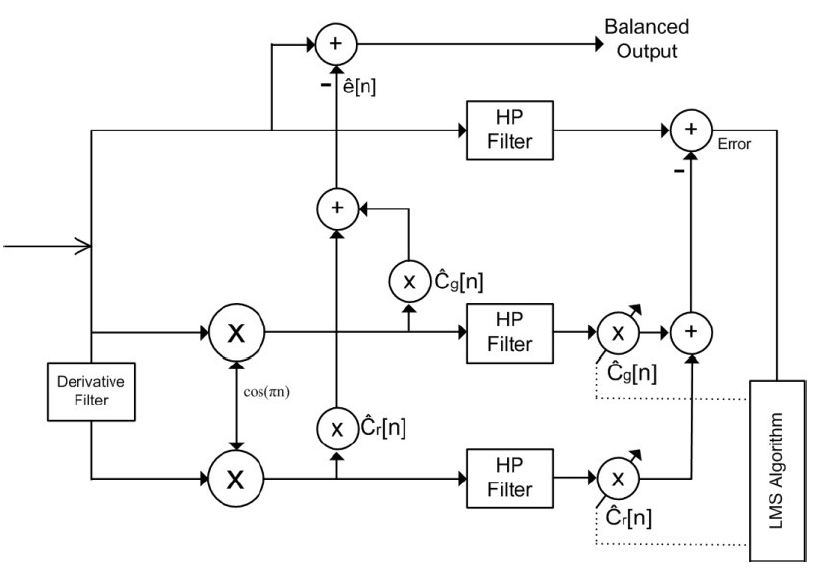
請注意，現有結構背后的基本觀察（如圖 8 所示）是通過使用不發生失配的 TI-ADC 對輸入信號 x（t） 進行過采樣，我們應該能夠觀察到一些沒有信號的頻譜區域能量存在。然而，由于兩個通道之間的增益和時間偏移，在這些頻段中會出現一定數量的不需要的能量（稱為失配帶寬）。通過過濾和最小化失配帶寬中的信號頻譜幅度，可以自適應地識別和糾正失配，為此，LMS 算法是一個自然的選擇。輸入信號的低通特性的假設，以及采樣頻率的知識，

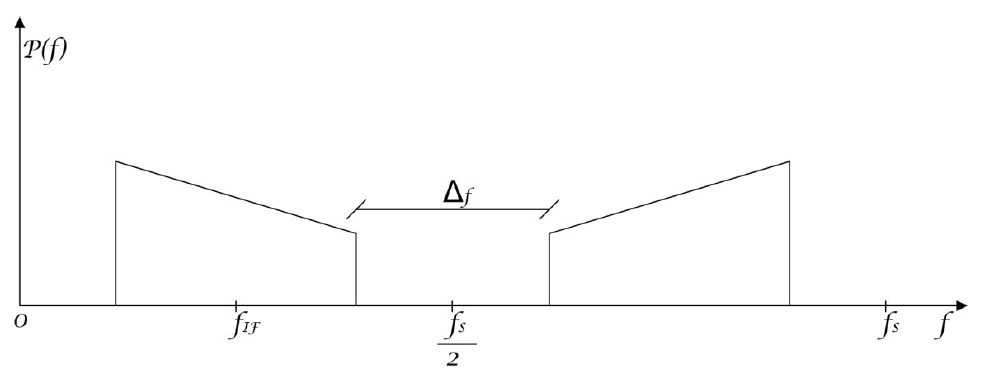
我們在此回憶一下，在只有一個模數轉換器的普通數字接收器中，采樣頻率的選擇是為了滿足方程 1 中的等式。（1） 其中 Δf 稱為過采樣因子。請注意，它表示采樣后兩個信號頻譜副本之間的差距（見圖 9）。我們希望使這個因素盡可能小，與數字接收器必須處理的后續濾波任務的要求兼容。在實際的接收器中通常

0 《 Δf ≤ 2fIF – BW （2）

最常見的是四分之一速率采樣：fIF/fs=1/4。請注意，Δf 》2fIF-BW 的情況對應于信號的最大頻率分量 fmax 和 fs/2 之間的間隙，該間隙大于第一個奈奎斯特中零頻率和最小信號分量 fmin 之間的間隙區。這個假設通常被丟棄，因為它意味著帶寬的浪費。

當使用雙通道 TI-ADC 時，每個臂上使用相同的采樣頻率 fs0，1=fs/2，其中一個臂中的初始采樣時間的時移等于 1/fs。這些采樣頻率違反了奈奎斯特采樣定理，因此，位于第二奈奎斯特區域的副本的負側出現在第一奈奎斯特區域。如果結構中不存在不匹配，則應在多路復用器的輸出處自動抑制此副本。我們之前指定，當 fIF/fs=1/4 時，Δf/2 代表 fmax（輸入信號的最大頻率）與 fs0，1 之間的差距。它還表示來自第二奈奎斯特區的負副本的零頻率和最小頻率之間的差距。在這種情況下，兩個副本，屬于第一個奈奎斯特區的正數和屬于第二個奈奎斯特區的負數將彼此完全重疊，并且很難想象由時間和增益偏移引起的不匹配。在Δf 《2fIF-BW的情況下，屬于第二奈奎斯特區的信號副本的負側將部分重疊在屬于第一奈奎斯特區的正信號部分上；事實上，它將接近于零。很明顯，對于上述兩種情況，我們不會在 fmax 和 fs0，1 之間產生不需要的能量。這正是定義了失配帶寬并且設計了當前 TI-ADC 識別和校正結構的光譜區域。這也是當前架構不適用于中頻采樣通信場景的原因。此外，當應用低速率采樣時，不匹配帶寬的位置變得更加不可預測。

我們開發了一種通用解決方案，它獨立于調制格式、信號帶寬和總體選擇的采樣頻率。通過使用我們的解決方案，我們能夠將偽像電平降低到 80dB 以下，這在該領域是獨一無二的（請參閱本節末尾的參考資料）。

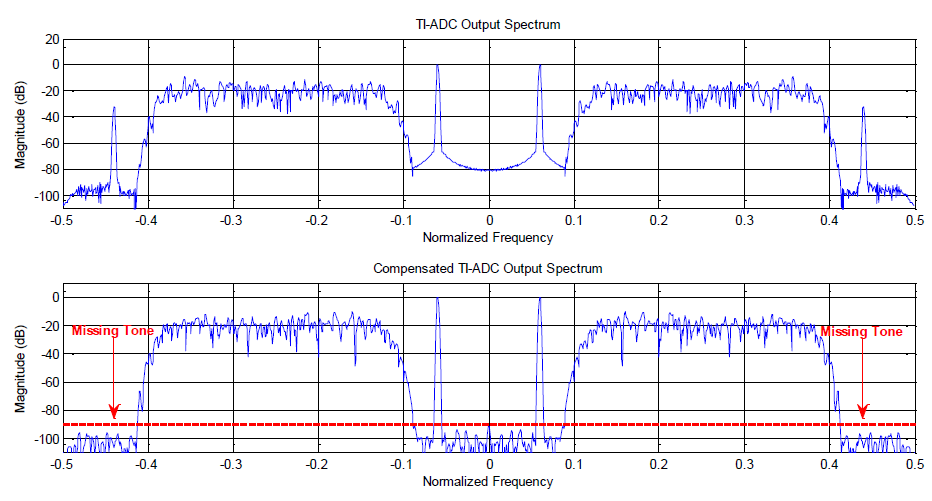
在圖 10 的第一個子圖中，顯示了由具有增益和時間偏移的雙通道 TI-ADC 處理的 QPSK 信號的頻譜。此示例的時序偏移為 r0=0 和 r1=0.04，這對應于總采樣時間的 4% 誤差。請注意，如果與現實場景相比，此時間偏移相當大，但同樣對于這種極端情況，識別和校正結構仍然提供良好的衰減水平。本示例選擇的增益偏移為 g0=0 和 g1=0.05，這對應于 TI-ADC 第二臂上的 5% 誤差。請注意，應該屬于第二個奈奎斯特區域的 QPSK 信號副本出現在第一個區域中。該復制品完全疊加在信息信號上，因此無法證明其在該信號頻譜上的存在。在圖 8 的第二個子圖中，顯示了補償器輸出端的信號頻譜。在此圖中，我們為測試結構功能而插入的音調不存在于信號頻譜的外側（高頻）；通過使用建議的估計和補償結構，我們能夠將其能量降低到 90dB 以下。該值由圖中紅色虛線表示。

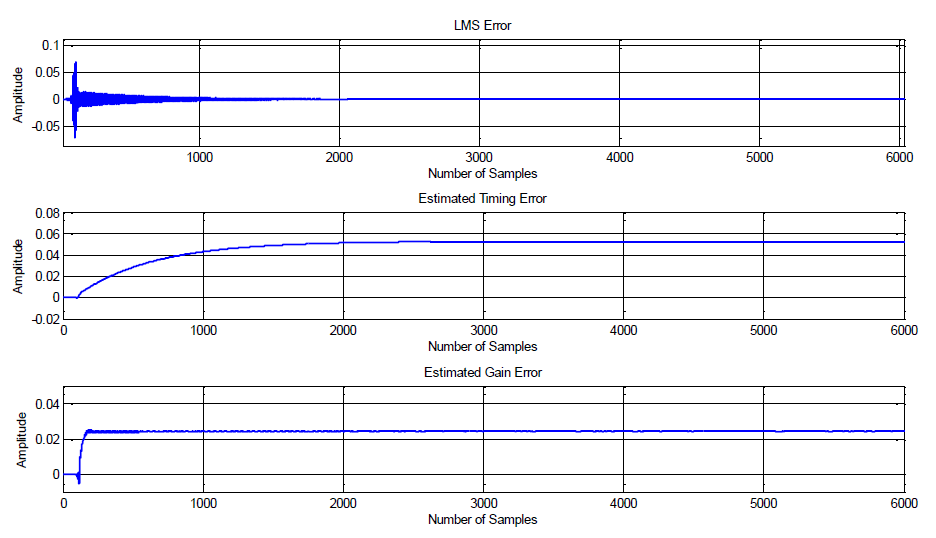
圖 11 顯示了估計過程的收斂行為。當時序和增益誤差收斂到正確值時，LMS 誤差最小。本例中 LMS 算法的選擇步長為 μ=0.04。由于已應用 LMS 算法來最小化確定性正弦音的能量，因此誤差的收斂值具有零均值和零方差。在圖 11 的第二個子圖中，顯示了與時序誤差相關的權重的收斂行為。類似地，圖 11 的第三個子圖顯示了與增益誤差估計相關的權重的收斂過程；該過程在 200 個樣本后收斂到 0.025，這是對應于 ADC 增益平均值的理論預期值。

為了證明我們無法在頻譜圖中直接看到的失配抑制程度，我們在圖 12 中比較了解調的 QPSK 星座（校正后）與傳輸的星座。解調過程是通過將信號通過希爾伯特變換來實現的，這使我們能夠訪問解析信號及其復包絡。然后在數字下變頻器中通過復外差對信號進行下變頻。最后，將具有適當時間對齊但未進行相位校正的匹配濾波器應用于復基帶信號，以最大化其信噪比。此過程產生的星座圖顯示在圖 12 的第三個子圖中，以及第一個子圖中的傳輸 QPSK 星座和第二個子圖中 TI-ADC 輸出處的損壞 QPSK 星座。清楚地表明，TI-ADC 不匹配導致匹配濾波器輸出星座點周圍的方差云增加。通過使用所提出的結構，方差云被完全去除。

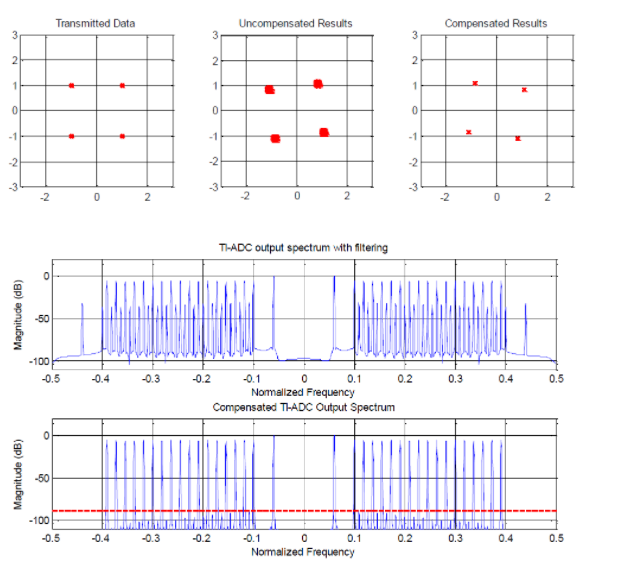
在圖 13 中，我們在歸一化頻率軸上生成了 17 個等距正弦波，頻率范圍從 0.1 到 0.4。增益和時間誤差與先前模擬中使用的相同。時間和增益偏移的組合效應可以在圖 13 的第一個子圖中可視化，其中來自第二個奈奎斯特區并在多路復用器的輸出處未抑制的折疊頻譜出現在構建的信息信號的譜線之間。圖 13 的第二個子圖顯示了補償后獲得的頻譜。在這里，我們可以清楚地認識到光譜偽影顯著減少。我們還注意到包含偽像殘余物的殘余光譜，其抑制程度與探測信號不同。這些偽影低于 -90dB，如同一圖片中的紅色虛線所示。請注意，在補償之前，影響信號的雜散峰值的對數最大幅度為 -30.2dB；補償后的最大振幅為-90dB。這個結果清楚地表明我們的結構能夠獲得大約 60dB 的改進。

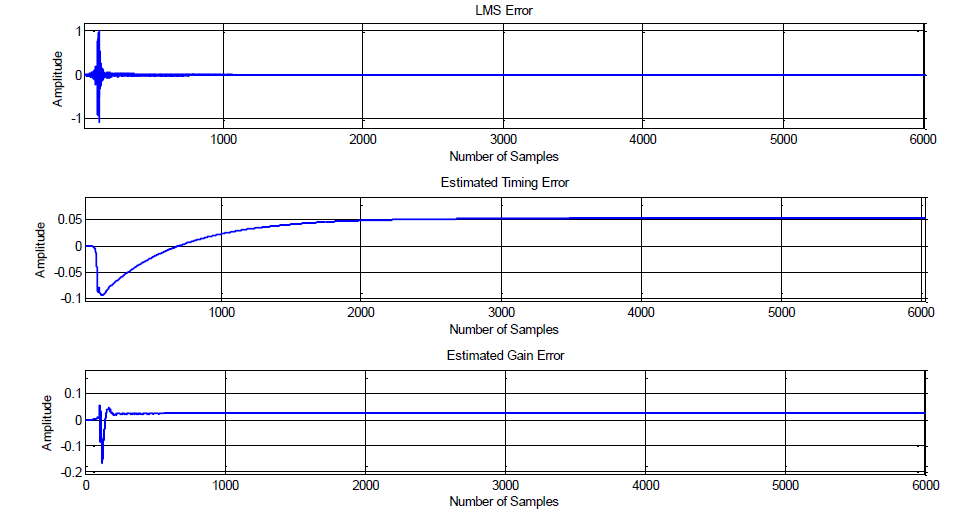
為完整起見，圖 14 顯示了 LMS 收斂行為，以及正弦波頻譜情況下的時間和增益偏移估計。用于嵌入識別結構的 LMS 算法的 μ 值與圖 10 的模擬中的相同。

參考

［1］ fred harris，多速率信號處理，Prentice Hall，2004 年。

［2］ S. Saleem 和 C. Vogel，“雙通道時間交錯模數轉換器中基于 LMS 的時序失配識別和補償” ，在過程中。IEEE Norchip Conf.，第 14 頁，2007 年 11 月。

［3］ C. Vogel、S. Saleem 和 S. Mendel，“M 通道時間交錯 ADC 中增益和時序失配的自適應盲補償”，Proc。第 14 屆 IEEE ICECS，第 4952 頁，2008 年 9 月。

［4］ S. Huang，BC Levy，“兩通道時間交錯 ADC 的時序偏移和增益失配的自適應盲校準”，IEEE Trans。關于電路和系統-I：常規論文，卷。53，沒有。6，第 1278-1288 頁，2006 年 6 月。

［5］ P. Satarzadeh、BC Levy 和 PJ Hurst，“雙通道時間交錯 ADC 帶寬失配的自適應半盲校準”，IEEE Trans。關于電路和系統-I：常規論文，卷。56，沒有。9，2009 年 9 月。

［6］ J. Goodman、B. Miller、M. Herman、G. Raz 和 J. Jackson，“時間交錯模數轉換器的多相非線性均衡”，IEEE 期刊信號處理，卷。3，沒有。

3，2009 年6 月。［7］ F. Palmieri、E. Venosa、A. Petropulu、G. Romano 和 P. Salvo Rossi，“軟件定義無線電接收器的稀疏采樣”，Proc。SPAWC 2010 – 第 11 屆 IEEE 無線通信信號處理進展國際研討會，2010 年 6 月 20-23 日，摩洛哥馬拉喀什。

［8］ E. Venosa、fred harris 和 F. Palmieri，“軟件無線電：采樣率選擇、設計和同步”，Springer Science + Business Media， LLC 233 Spring Street， New York， NY 10013， USA， 2011。

［9 ］ F. Palmieri、E. Venosa、G. Romano、P. Salvo Rossi 和 A. Petropulu，“數字通信信號的低速率均勻采樣”，提交給 EURASIP 無線通信和網絡雜志。

［10］ Mikko Waltari 和 Kari Halonen，低壓和高速 A/D 轉換器的電路技術，Kluwer Academic Publishers，2002 年。

編輯：hfy