電壓,導體的電阻或通過電線的電流是可以通過使用測試儀容易地測量的量。但是,如果您需要了解一個手工電容器的容量或不讀取其板數據的電容器,則需要另一種測量儀器,即“電容表”,它通常很昂貴。有許多方法可以測量任何難度和精度的未知容量值。讓我們看看如何借助理論輕松地測量這兩個電量。
正弦交流電壓下的電容器
當我們向電容器施加直流電壓時,如果瞬變消失,則其行為就像開路一樣。相反,當電容器處于正弦狀態時,它的行為不再像開路那樣,而是開始吸收電流,呈現出以歐姆表示的“電容電抗”。該分量類似于電阻。通過使用此原理,我們可以很容易地計算出未知電容器的值,并記住其電抗公式為:
Xc = 1÷2πfC
如果電容器受到正弦周期信號的影響,可以通過一些措施和一些方程式計算出其電容值。
方波電壓
電容器方波電容器的行為不同。方波不存在電容電抗。電抗的概念本身取決于正弦信號的存在。由于方波信號是無限正弦波的總和,因此不能顯著增加不同頻率下正弦波的電抗。因為(理想)電容器是線性的,所以我們可以將方波分解成正弦分量,找到每個分量的相關正弦電壓,然后將這些電壓相加得出總電壓。但是,此測量非常復雜,建議以其他方式更改策略并測量其電容值。
使用的策略
要測量電容器的電容,我們使用一種簡單的方法:我們使用由CD40106反相邏輯門和RC網絡組成的振蕩器生成方波。通過更改C的值(未知),顯然可以獲得不同的頻率。只需對這些值進行“曲線擬合”即可找到一個好的公式,該公式描述了所產生的頻率與要顯示的電容器的值之間的關系。
電氣原理圖
這是帶有兩個電氣原理圖的兩種不同解決方案。第一張圖專用于那些具有頻率計并可以使用該儀器測量頻率的人。它簡單得多,幾乎不需要電子元件。另一方面,第二個接線圖適用于那些沒有頻率計而是簡單的測試儀,甚至是便宜的測試儀的人。因此,該方案與第一種方案相似,但是使用了一個額外的頻率/電壓轉換器來讀取普通測試儀上的值。
具有頻率計的用戶
的第一個接線圖第一個接線圖更簡單,如圖1所示。心臟由集成電路CD40106表示,集成電路CD40106與C1和R1一起生成周期性方波信號。頻率由C1和R1決定,但是由于R1是固定的,因此它與未知電容器成比例地變化。第一邏輯門(X1)產生信號,第二邏輯門(X2)用作阻抗緩沖器。這樣,連接到其輸出的任何負載都不會改變所產生信號的頻率或幅度。后者在電阻R2上可用,準備使用頻率計在頻率上進行測量。
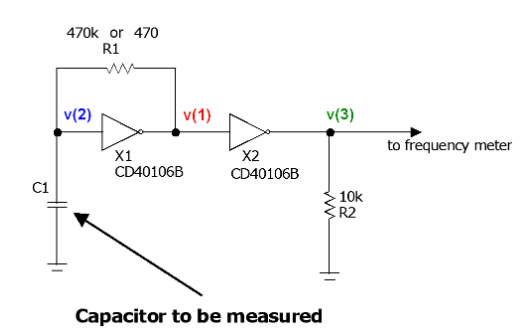
圖1:帶有頻率計的設備的第一個接線圖
圖2顯示了電路上這些點處的信號圖:
- 電容器上信號的藍色曲線圖(V2)
- 第一個逆變器輸出上的信號的紅色曲線圖(V1)
- 第二個逆變器輸出處的平方信號的綠色曲線圖(V3)
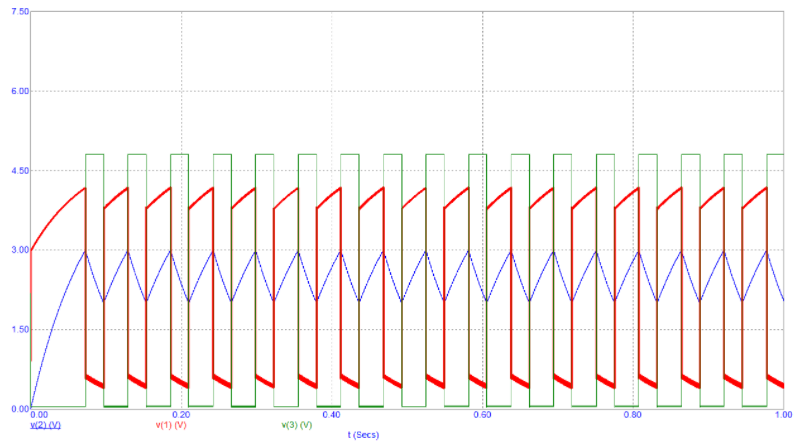
圖2:電路各個點的信號圖
標度1 pF / 100 nF
下表包含所有理論頻率值,這些值僅通過更換電容器C1即可測得。對于此測量范圍(介于1 pF和100 nF之間),電阻R1必須為470 k。關系圖如圖3所示。
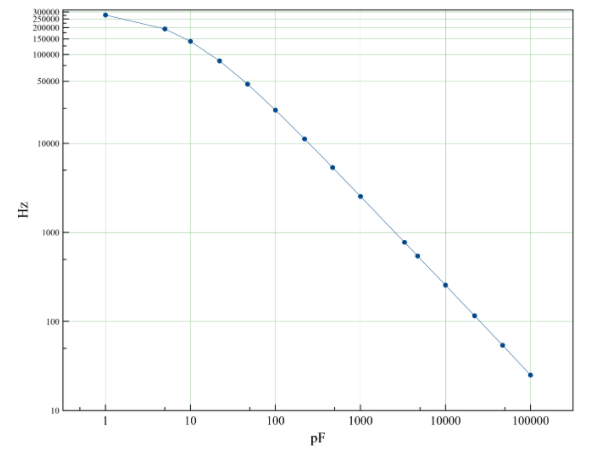
圖3:電路電容和頻率之間的關系的對數圖(R1 = 470 k)
| F | 赫茲 |
| 1個 | 277,393 |
| 5 | 193,611 |
| 10 | 140,449 |
| 22 | 84,667 |
| 47 | 46,419 |
| 100 | 23,706 |
| 220 | 11,245 |
| 470 | 5,367 |
| 1,000(1 nF) | 2,542 |
| 3,300(3.3 nF) | 775 |
| 4,700(4.7 nF) | 544 |
| 10,000(10 nF) | 256 |
| 22,000(22 nF) | 116 |
| 47,000(47 nF) | 54 |
| 100,000(100 nF) | 25 |
對于該值范圍,描述電容和頻率之間關系的兩個公式如圖4所示。這是兩個非常復雜的公式,它們是從非線性曲線擬合的高級過程中獲得的。
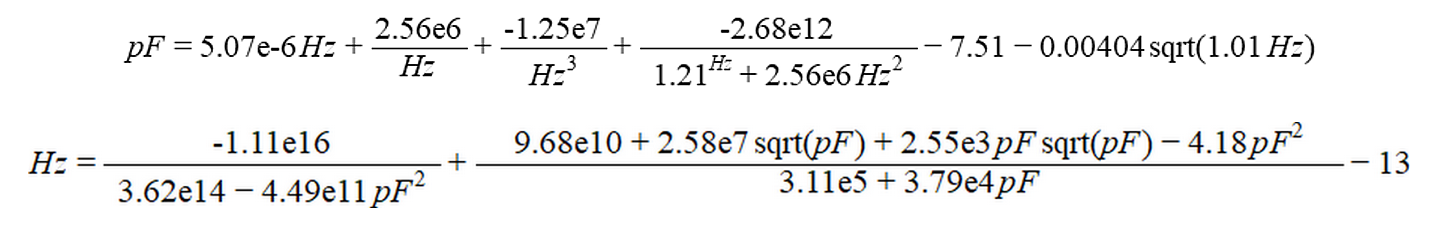
圖4:描述兩個量之間關系的兩個公式
100-nF / 100-μF標度
下表包含替換電容器C1的所有測得的理論頻率值。對于此測量范圍(介于100 nF和100 μF之間),電阻R1必須為470Ω。關系圖如圖5所示。
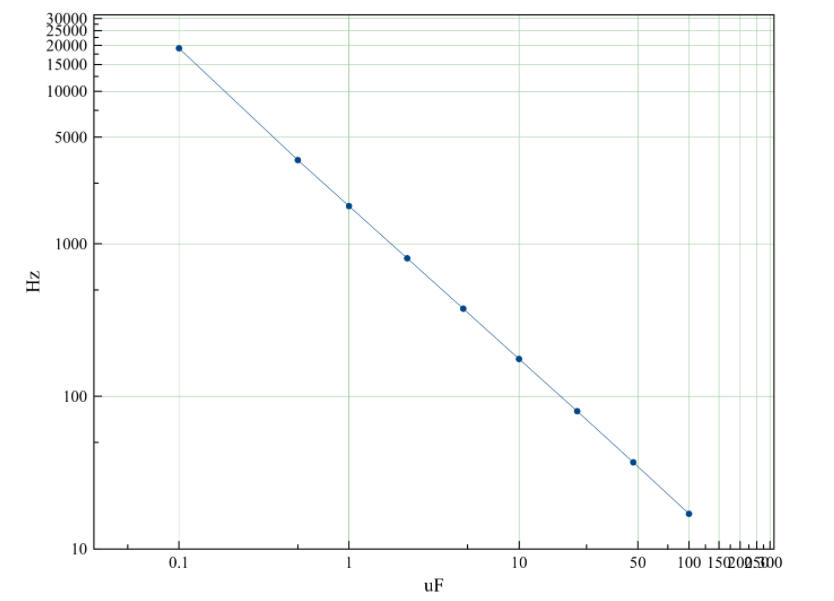
圖5:電路電容和頻率之間的關系的對數圖(R1 = 470Ω)
| μF | 赫茲 |
| 0.1 | 19,139 |
| 0.5 | 3,540 |
| 1個 | 1,768 |
| 2.2 | 804 |
| 4.7 | 376 |
| 10 | 176 |
| 22 | 80 |
| 47 | 37 |
| 100 | 17 |
對于該值范圍,描述電容和頻率之間關系的兩個公式如圖6所示。
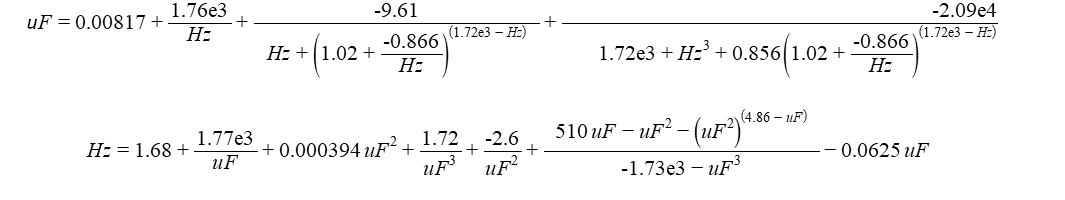
圖6:描述兩個量之間關系的兩個公式
?Figure 7示出了方波發生器電路和頻率米之間的簡單布線。對于測量儀器而言,重要的是能夠讀取周期性方波或矩形波信號的頻率。

圖7:方波發生器和頻率計之間的接線
僅具有測試人員的
用戶的第二布線圖僅具有測試人員的用戶可以實施第二種解決方案。連接到第一個的附加電路將輸出頻率轉換為負電壓,可以由通用測試儀測量。與上一個電路相連的新電路是帶有“泵”二極管的脈沖重復頻率表。整個系統(參見圖8)使我們能夠根據要測量的電容C1獲得負電壓。
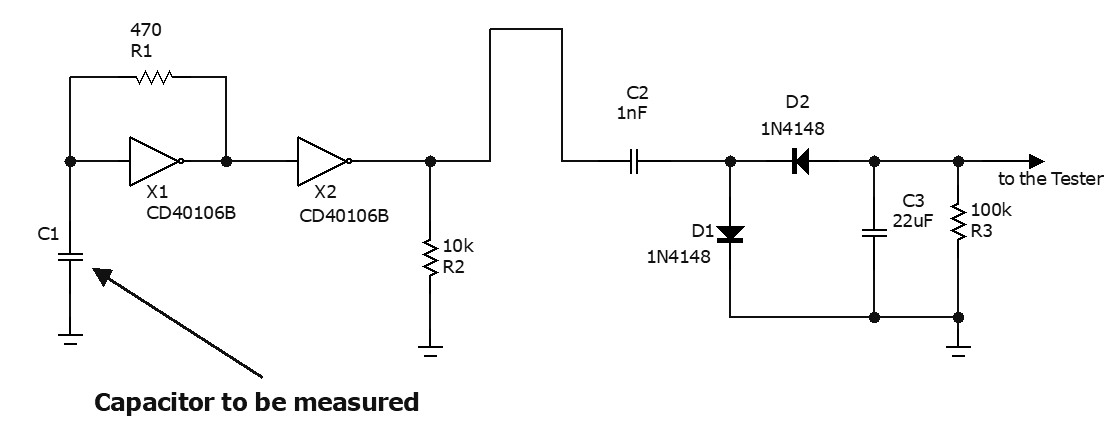
圖8:擁有簡單測試儀的人員的第二個電路
正脈沖負載在最大電壓C2至D1處。在脈沖之間的間隔中,輸入為0 V時,C2通過D2快速放電到大電容C3。因此,輸出電壓與接收脈沖的速度成正比。冷凝器C3類似于一個大罐,被R3慢慢排空。下表包含從不同測量收集的C1電容值不同的數據。該值是指介于100 nF和100 μF之間的電容。為了獲得穩定的電壓值,必須等待幾秒鐘的瞬變,如圖9所示。
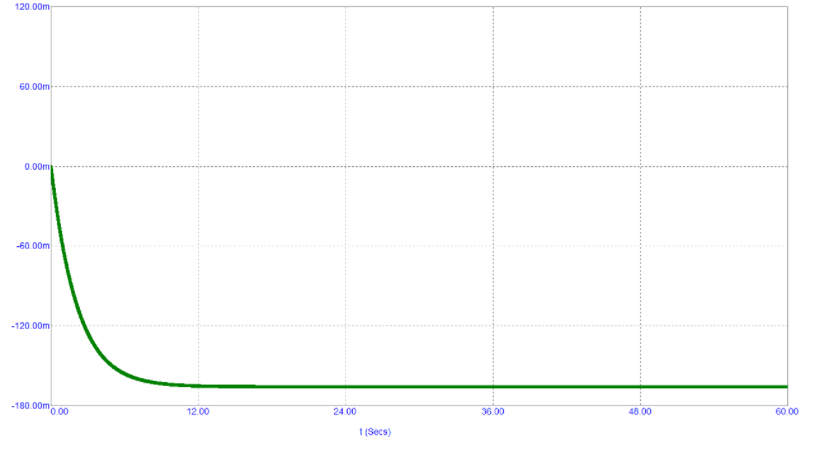
圖9:從測量開始幾秒鐘后獲得的穩定電壓值。
| μF | 測試儀R3上的電壓(mV) |
| 0.1(100 nF) | –2,655毫伏 |
| 0.47(470 nF) | –1,185毫伏 |
| 1個 | –663.70毫伏 |
| 2.2 | –334.43毫伏 |
| 4.7 | –165.62毫伏 |
| 10 | –80.36毫伏 |
| 22 | –37.16毫伏 |
| 47 | –17.48毫伏 |
| 100 | –8.21毫伏 |
對于該值范圍,描述電容和輸出電壓之間關系的公式如圖10所示。
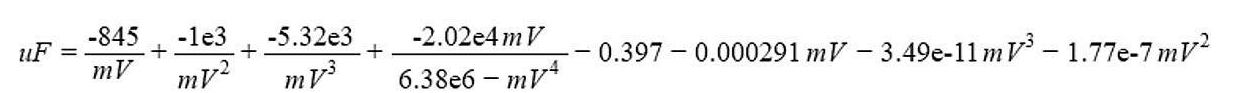
圖10:描述兩個量之間關系的公式
?Figure 11示出了方波發生器電路中,頻率/電壓轉換器,并且在VDC模式下配置的正常測試器之間的布線。這是一個非常簡單的連接,需要在簡單的PCB內構建系統。
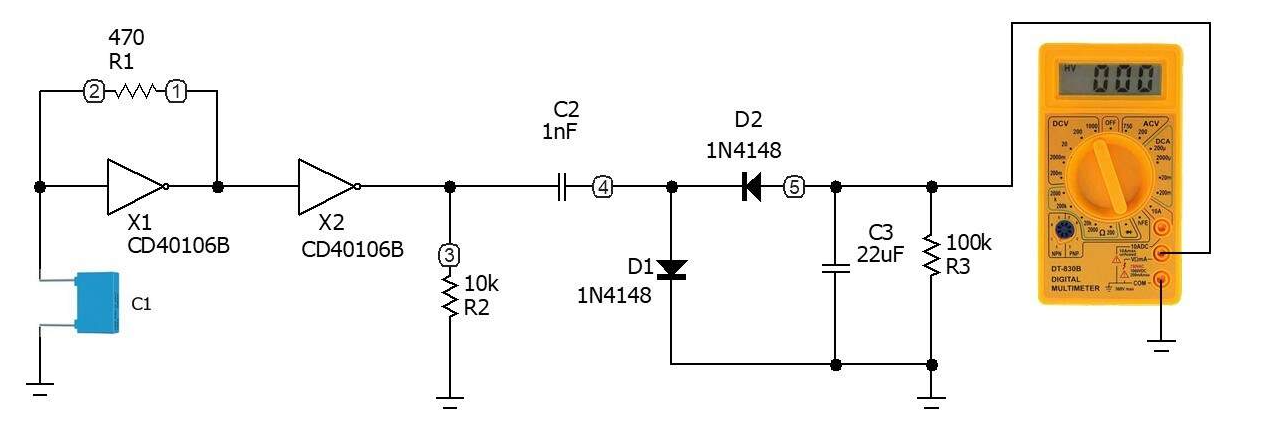
圖11:方波發生器,頻率/電壓轉換器和普通測試儀之間的接線
結論
本文中介紹的測量與各種SPICE模型的仿真有關。建議在實際電路上收集數據。用戶可以根據所需的電容間隔自由創建自己的數學模型,還取決于瞬態的等待時間和RC時間常數,這可能會產生較長的等待時間。我們建議您嘗試根據需要更改電子組件的值。如果在應用公式時遇到困難,則可以簡單地查閱收集的數據表,然后通過內插法找到真實的經驗數據。為了對數據進行曲線擬合,可以使用任何帶有此可用選項的數學和統計軟件。本文的主要目的是演示電子與數學是如何緊密聯系在一起的。該項目可以針對不同的目的和功能進行任何修改或改進。
編輯:hfy
-
集成電路
+關注
關注
5387文章
11534瀏覽量
361647 -
電容器
+關注
關注
64文章
6217瀏覽量
99541 -
振蕩器
+關注
關注
28文章
3832瀏覽量
139041 -
正弦交流
+關注
關注
1文章
17瀏覽量
8663 -
方波信號
+關注
關注
0文章
28瀏覽量
14182
發布評論請先 登錄
相關推薦




 如何使用集成電路40106發現未知電容
如何使用集成電路40106發現未知電容










評論