摘要四元數是哈密頓對二元數，即復數，的推廣，其成功開啟了近世代數的大門。哈密頓將四元數的純虛部稱為vector，漢譯矢量。由三維世界矢量的四元數乘積引入了點乘和叉乘的概念。麥克斯韋從泰特那里學會了四元數，針對微分矢量運算發明了散度和旋度的概念，三分量的普通四元數世界矢量被麥克斯韋和亥維賽德用于電磁學的表述，于是有了我們今天熟悉的麥克斯韋方程組的形式，吉布斯和亥維賽德由此各自獨立地發展出了矢量分析。矢量分析是對嚴謹的四元數代數的實用主義裁剪，用處是明顯的，危害也是巨大的。亂糟糟的?點乘-叉乘讓電-動力學成為大多數物理類學生的噩夢。泰特為捍衛四元數進行了艱苦卓絕的斗爭，但結果還是矢量分析大行其道。哈密頓追求建立一般的多重代數，吉布斯試圖將三維矢量分析推廣，加上格拉斯曼創立的線性展開的學問以及佩爾斯創立的線性結合代數，于是有了線性代數。差不多同時期誕生的矩陣理論、格拉斯曼代數和克利福德代數同它們都有親密的內在聯系，也都是物理表述的數學基礎。弄清楚四元數、矢量分析和線性代數背后的代數學知識和相互間的關系，普通物理教科書中的數學表述可能就不那么令人迷惑了，也能理解為什么電-動力學里的矢量叉乘又叉乘怎么在量子力學里——據說波函數也是矢量——咋就不見了。順便說一句，矢量之所以是矢量在于它所遵循的代數結構，它無需有方向、甚至也可以沒有長度。

01 一頭霧水的電-動力學符號

筆者愚魯，大學物理成績慘不忍睹，其中又尤以電-動力學2)一門為甚。有句俗話，說“沒哭過長夜，不足以言愛情”。套用這句俗話，筆者想說“沒為亂糟糟的?點乘-叉乘公式懷疑過人生，不算學過電-動力學。”筆者當年純粹是為了求生才不得已死記硬背過那些莫名其妙的公式，至于它們有什么數學含義、對應什么物理圖像、有何道理可言，筆者完美地繼承了課本作者和授課老師的茫然無知。為了增加大家的惡心直視感，現將 John David Jackson 著《經典電-動力學》(這本國際上流傳甚廣的電-動力學教科書，Classical Electrodynamics, 3rdedition, John Wiley & Sons, Inc. (1999)，我給高度差評！)一書里的所謂 vector formulas 附錄照錄如下：

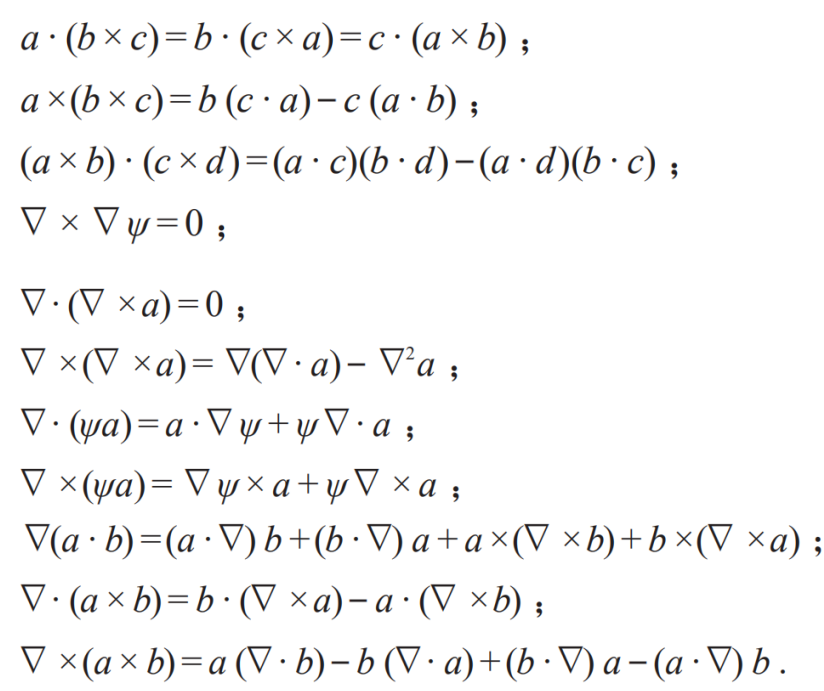
對于三維位置vectorx，有 ? ?x= 3；? ×x= 0。

上表中的a，b，c，以及x，是vector。一般《電-動力學》教科書里都會列這個表，我猜是為了方便讀者查找。那為什么要方便查找呢？當然是因為就知道你不明白也記不住啊！這大概是一般《電-動力學》教科書作者的預設立場。有趣的是，這些作者一般也不告訴我們這里討論的是特定的三維vector而不是線性代數里的任意維vector，也不是量子力學中的波函數ψ那種取復數值但模總為1的vector，兩個波函數組成的二分量怪物是旋量但老是被誤以為是矢量。至于這里的?點乘-叉乘公式來自這種特定的三維vector自身的代數性質，在這類書中更是不見蛛絲馬跡。值得警惕的是，一般(英文)書中會把vector定義為既有長度又有方向的量，故有漢語矢量的說法和英文的 arrow notation ，更是錯得離譜。矢量屬于這樣的集合，其中任意兩個元素a1，a2的線性疊加λ1a1+λ2a2，λ是屬于某種數域的標量，都在這個集合里，即該集合對于線性疊加是閉合的。至于vector是否有模(長度)，兩個vector之間能否定義夾角(方向)，那可不一定。

上面所列公式，學問上屬于矢量分析(vector analysis)的范疇。由于筆者沒學過代數學的基礎，更沒學過近世代數(modern algebra)，因此對上述公式除了按照所給模樣死記硬背以外，別無他法。如果有點代數基礎的話，人們會發現上面的公式問題多多。首先，注意到有兩種乘法，一種是對易的，a?b=b?a；一種是反對易的，a×b=-b× a 。既然涉及反對易關系，這得是一種特殊的非交換代數了。再看看公式a×(b×c) =b(c?a)-c(a?b)，公式里的括號很重要，它在強調這個表達式是非結合的(non-associative)，a×(b×c) ≠(a×b)× c。也就是說，這個矢量分析涉及非交換的(non-commutative)和非結合的計算，那還不步步是陷阱啊。注意到由于一般教科書作者也不知道這些公式的意義，因此當右側出現四項的時候就不 知 道該如何放置才好了。比如，前述公式里的?×(a×b) =a(??b)-b(??a) +(b??)a-(a??)b，若我們知道具體某項的來源與意義，寫成 ?×(a×b) =(??b+b??)a-(??a+a??)b的形式就容易明白的多，右側各括號里的加號來自微分算符的性質，中間的減號來自叉乘的反對易性質，一目了然。

在第一次接觸到上述電-動力學公式列表的許多年后，筆者注意到此處的矢量只是矢量這個概念的特例ai+bj+ck，乃是 ordinary quaternion world vector (普通四元數世界矢量)，它和四元數這種特殊的超復數(hypercomplex number)有繼承關系，也和線性代數有內在的關聯。弄清楚了四元數、矢量分析、線性代數之間的關系，以筆者有限的物理見識，可以斷言大學普通物理里的許多內容都會變得明晰可愛起來。比如，電磁學中麥克斯韋方程組的微分形式，剛體的轉動表示與角動量，量子力學里的自旋，相對論量子力學的旋量表示，你都可以在四元數——那是矢量分析的母體——里找到內在的、一致的當然也是簡單的理解。

02 哈密頓、復數與四元數

人們在解一元三次方程的時候，會遇到根號下出現負數但又不能一扔了之的問題(解一元二次方程時可一扔了之)，于是不得不保留了負數的平方根。引入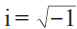作為單位虛數(錯，應該是?ii = -1)，z= a+ bi 這類結構的數稱為復數。大約在 1830年，25歲的愛爾蘭數學家、天文學家哈密頓(Sir William Rowan Hamilton，1805—1865. 就是 Hamiltonian 里的那個哈密頓，見圖1)認為把復數寫成一個實數加一個虛數的做法是有誤導性的。筆者當年也注意到復數加法?(a+ ib) +(c+ id) =(a+ c) + i(b+ d) 里的加號意義不一樣，但也就到此為止，不敢質疑也沒有能力質疑【怪我咯！】。哈密頓認為 z?=?a?+?bi 里的這個加法符號只有形式意義，關于復數重要的是它遵循的算法而不是你把它表示成什么樣子。比如我們可以把復數表示成矩陣的形式，

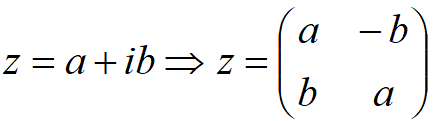
，它遵循與復數同樣的加法和乘法，可以表示二維平面的幾何。把復數寫成矩陣，則模為1的復數，其矩陣一般形式為 z=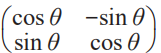，這就是二維空間的轉動變換哦，復數乘積就有表示二維平面內轉動的功能。當然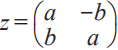，這樣的形式還和保角變換有關系、還聯系著哈密頓方程和辛幾何(symplectic geometry)，等等，此處不提【感慨：不要小瞧你一年級時學過的加法，那里面有太多的東西你聽都沒聽說過】。總而言之，哈密頓意識到復數是一種遵循具體算法的具有兩個元素的數而已，寫成(a,b)即可，他將之稱為代數偶素(algebraic couple)，現在也叫二元數(binarion)。

圖1 哈密頓爵士，一個筆者認為其數學和物理成就均高于牛頓的人

復數，或者叫二元數，代數偶素，是個非常有力的數學概念，除了用于解代數方程還能描述二維空間轉動。可我們生活在三維空間啊，哈密頓想到，應該構造triplet，三重數或者三元數，來描述物理空間里發生的現象。仿照二元數，三元數z=a+ib+ jc，有兩種虛部i2= j2=-1 ，看似沒有多少難度。然而，求三元數的乘積時會出現ij和ji項，這是新元素，帶來了新問題。令 ij = ji = 0或者 ji =-ij 都消除不了任意三元數乘積以及任意三元數模平方乘積中出現的問題。這讓哈密頓很苦惱，相關研究反反復復地放下又拾起，轉臉13年過去也未能畢其功。

1843年10月16日，哈密頓腦海中靈光一現：如果是四元數的話，很可能會使得數的乘積和數模平方的乘積也分別具有數和數模平方的形式。也就是說他需要研究的是 z = a + ib + jc + kd 形式的數，為此需要引入第三個虛數k2=-1，此三個單位虛數滿足關系 ij = k，jk = i，ki = j；ij =-ji，jk =-kj，ki =-ik【記住這兩個關系，這是矢量分析重點要繼承的關系】，i2= j2= k2= ijk =-1。構造三元數和四元數，放棄根深蒂固的乘法交換律是關鍵一步，確實需要勇氣和膽識。后來我們知道，哈密頓想要的是具有除法的三元數，根本就不存在，四元數的代數才是除法代數——除法代數只有實數、二元數、四元數和八元數這四種情形，此為Hurwitz定理。兩個四元數的乘積還是四元數，用這個性質可以輕松證明任意兩組四個整數平方和之積還是四個整數的平方和——這就是個演算而已，都不能算證明。

四元數的純虛部，即r=xi +yj+zk，可以描述三維空間，哈密頓稱其為vector (漢譯矢量。再次提請注意，此處的vector是數！)，確切地說是ordinary quaternion world vector，普通四元數世界矢量3)。我們要牢記r=xi +yj+zk 這樣的矢量是實部為零的四元數，還不是什么有方向的量。計算(xi +yj+zk)(ai +bj +ck) =-(xa+yb+zc) +(yc-zb)i+(za-xc)j +(xb-ya)k，可見矢量的四元數積包括實部(哈密頓給起了個名字scalar，漢譯標量)和矢量部分，哈密頓將之分別稱為矢量的點乘(標量積)和叉乘——這是哈密頓構造出四元數的當天得到的結果。上式的矢量乘法用到了四元數之虛數的性質 ij = k，jk = i，ki = j，這反映的就是所謂的三維空間矢量叉乘的右手定則。矢量叉乘的A × B = -B × A 性質其實就來自四元數乘法的規則 ij = -ji， jk = -kj，ki = -ik這個和排列(permutation)的正負符號交替，求矩陣值時表達式里的正負符號交替都有關。1846年，哈密頓甚至引入了

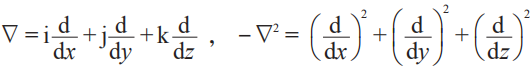
符號。我們看到哈密頓實際上有了后來的矢量分析的全部內容(he could manage the full panoply of quaternion operations with ease)，但是，哈密頓是有哲學素養的、嚴謹的數學家，犧牲數學的優雅與嚴謹去迎合物理實用的事兒他干不來，他可舍不得為自己的四元數弄個不倫不類的簡化版。換了你，你也舍不得——把大家閨秀當燒火丫鬟使喚的，那得是個粗人！科學，尤其是應用科學的發展，或許需要這樣的粗人，當然不能粗到不憐惜數學的程度。

哈密頓關于四元數的思想，見于他的兩本書 Lectures on the quaternions 和 Elements of quaternions(圖2)，后一本本來打算是作為前一本的簡化版的，結果越寫越深、越寫越厚，哈密頓對數學的態度由此可見一斑。更多內容，請參閱拙作《磅礴為一》和《云端腳下》4)中關于復數、四元數與哈密頓的相關章節。

圖2 哈密頓的經典著作《四元數原本》

03 麥克斯韋、吉布斯、亥維賽德與矢量分析

哈密頓有位親學生蘇格蘭人泰特(Peter Guthrie Tait，1831—1901，圖3)，其是著名的數學物理學家、熱力學的創始人之一5)。泰特當然是四元數的強烈擁護者，是四元數的傳播者，寫過Treatise on quaternions. 泰特有個同班同學叫麥克斯韋(James Clerk Maxwell，1831—1979)，麥克斯韋從泰特那里學到的四元數，當然明白四元數的物理意義，故他支持四元數。麥克斯韋1871年曾撰文On the mathematical classification of physical quantities (論物理量的數學分類)，筆者以為，這篇論文是科學史上的重要文獻——多少電磁學、電-動力學文獻根本不懂麥克斯韋，誤把E，B當成了同樣的數學對象了！麥克斯韋指出，哈密頓把四元數之虛部的乘積結果分為標量部分和矢量部分具有重要的物理意義！麥克斯韋甚至認為四元數是朝向獲得關于空間的量的知識邁出的一大步，可同笛卡爾引入坐標系相媲美。許多物理現象有相似的數學表達，如果關注這些數學形式，就能對物理現象有更好的理解6)—— 不得不說，麥克斯韋是真有洞見的物理學家。麥克斯韋接著討論哈密頓的微分矢量算符?，造出了 convergence 和 curl，即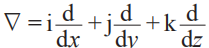作用于另一個矢量的點乘和叉乘，這兩個概念。麥克斯韋看到的是哈密頓的世界矢量表示空間里的物理現象的優點，而非是簡單的計算方法“…but it is a method of thinking…It calls upon us at every step to form a mental image of geometrical features represented by symbols！”

圖3 泰特

在麥克斯韋看來，四元數表示電磁學現象比用坐標更直接，這樣數學就能更多地解釋電磁學的特性。麥克斯韋的方案是同時使用坐標和四元數，即雙語(bilingual)方案。這么做的一個不方便的地方是，按照四元數的約定，矢量同自身的點乘(模平方)是負數，但是用坐標表示時那得是正數，這有點兒擰巴。用麥克斯韋自己的話說，這整個兒是 plough with an ox and an ass together (用牛和驢配套犁地)。嗯，這句話筆者作為莊稼人秒懂。

矢量分析的發明人是美國人吉布斯(Josiah Willard Gibbs，1839—1903)和英國人亥維賽德(Oliver Heaviside，1850—1925)，見圖4。吉布斯，就是吉布斯自由能的那個吉布斯，統計物理奠基人之一，他創造了統計物理這個詞兒，Made his field a well-nigh finished theoretical structure。亥維賽德把復數引入電路分析，故對將四元數用于物理沒有任何心理障礙，當前形式的麥克斯韋方程組就是他寫出來的，這是矢量分析的一大成就！這兩個人都是在閱讀麥克斯韋1873年的Treatise on electricity and magnetism (電磁學論)時，有感而發，認為有簡化或曰裁剪四元數以供表述電磁學的實際需求，最后各自獨立地發展出了矢量分析。閱讀麥克斯韋著作的吉布斯注意到，對于電磁學來說用不著保留整套的四元數代數，在1888年的一封信里他表明他決心發明矢量分析體系。吉布斯說他看出來就電磁學而言，矢量的點乘和叉乘保持在一個式子里不是個好主意(這一點上吉布斯錯了。嚴格的數學才能導致正確的物理)，他把叉乘和點乘當作兩個獨立的矢量操作。吉布斯于是構建了具有兩種乘法的矢量分析，以及微分算符?對標量和矢量的不同作用。吉布斯的靈感也是來自哈密頓本人的著作以及泰特的著作 Treatise on quaternions (論四元數)7)，但根本上還是麥克斯韋的思想。吉布斯的 Elements of vector analysis (矢量分析基礎)一書1881年面世，但到1901年才正式刊行，由其學生 Edwin Bidwell Wilson 編輯出版。同一時期，亥維賽德也是受麥克斯韋著作的影響在英國發展了矢量分析，于1881年和1883年以 The relations between magnetic force and electric current (磁力與電流的關系)為題發表了關于矢量分析的建議，系統的矢量分析在他1893年出版的Electromagnetic theory(電磁學理論)一書的卷一里。亥維賽德是在1888年聽說美國人吉布斯也發展了矢量分析的。

(三維物理空間的世界)矢量分析是出于表述電磁學、電-動力學的需要對四元數的實用主義裁剪，它帶來了一些便利和發展。但是，因為矢量分析是對嚴謹的四元數代數的實用主義裁剪，因此它的危害也是巨大的。眾多的一團漿糊似的電-動力學教科書和眾多筆者這樣的學電-動力學卻學了一腦子漿糊的人，就是證據！

四元數滿足普通數和二元數的交換律以外的所有代數運算規則，最重要的是它有除法。但是，剔出其中的矢量部分作為單獨的數學體系，問題可就麻煩嘍：(1)矢量有點乘和叉乘兩種乘法(甚至被有些人誤以為是獨立的)，且結果性質還不一樣，原則上它們都不是矢量啊(學物理的容易明白，兩個同樣對象的乘積，其量綱和自身就不一樣，它必然是不同性質的物理量！)，叉乘的結果只是在三維空間碰巧因為對偶關系可以當作矢量而已8)；(2)矢量叉乘不滿足結合律，這是大事情，是四元數沒有的大問題；(3)矢量沒有除法；(4)矢量模平方不滿足模平方乘積的恒等式；(5)矢量不為零但叉乘可能為零(太可怕了!)，這是代數最要避免的東西。這些問題都是因為(普通四元數世界)矢量只是四元數的局部，故有叉乘的可能性，而一般意義下的矢量就沒有叉乘運算了。比如，量子力學里的波函數可當作矢量，但沒有波函數的叉乘。后世的電-動力學教科書作者不理解那里面的(普通四元數世界)矢量及其算法的來源和性質，越抄越亂。

到了1893年，擁護四元數的人和擁抱新的矢量分析者之間的矛盾就冒出來了。作為四元數創始人的學生以及四元數研究者的數學家泰特，將矢量分析稱為hermaphrodite monster——不男不女的怪物！這話，真沒錯。泰特一人兩線作戰，分別支應四元數對坐標的戰場和四元數對矢量分析的戰場。在1890年On the importance of quaternionsin physics 一文中，泰特贊揚“四元數的自然特質。它以最顯而易見的方式越過坐標的任意性直接解釋了空間的物理特性(naturalness of quaternions which removed the arbitrariness of coordinatesand reveal the physical properties of space in themost obvious way)”。四元數是mode of representation (表示的模式)。當四元數后來成為算符表示轉動的時候，這一點就更清楚了。泰特把坐標比作大錘，有活兒得拿到錘子那兒去干，而四元數可比作象鼻子，靈活，啥活都能干，而且是主動式的。四元數是自然的！在他的 Treatise on quaternions的第三版序言中，泰特認為吉布斯是“one of the retarders of quaternion progress (四元數進展的主要遲滯者)”，現在看來，不幸被他言中。大量的物理系學生不懂四元數因而也就弄不清楚矢量分析里的代數思想當然就只能去死背公式的電-動力學課本，這極大地阻礙了電-動力學的教學！

而在另一方，亥維賽德因為自己是會四元數的，所以對四元數代數沒有任何負面評價，他只是認為四元數太難懂了，只能被 consummately profound metaphysicomathematician (學識極度淵博的形而上數學家)理解。但是，幾何學家凱萊(Arthur Cayley, 1821—1895)就不那么客氣了，他宣稱四元數只是一個使用坐標的特殊方法或者理論而已，對他來說四元數只能算是特殊的計算或者解析幾何。凱萊是代數大家，他怎么可能不知道四元數的偉大意義呢(這可是近世代數的開山之作)，他對四元數代數的這個態度，讓筆者捉摸不透。其實，四元數與矢量分析之爭也是比較奇怪的事兒。(普通四元數世界)矢量分析脫胎于四元數虛部的乘法，特殊的地方不過是微分算符，按說它們不該成為互為敵對的兩種方法。據說，因為矢量分析更直接貼近物理問題而為物理學家們所擁護，這話如今看來也未必有道理。首先矢量分析有內傷，學起來也很麻煩；至于更貼近物理問題，那得看是什么物理問題。描述轉動還是得用四元數！

補充一句，因為除法代數只有二元數、四元數和八元數，因此矢量叉乘只對三維矢量成立；如果放棄結果唯一性要求的話，對七維矢量也存在叉乘。其它維度空間里對應矢量叉乘的操作，是外積。

04 格拉斯曼、佩爾斯與線性代數

哈密頓從二元數，即復數，出發去構造triplet，結果落到了quaternion上。作為一個被形而上學武裝到牙齒的抽象派學者，哈密頓也一直尋找 polylets of ever higher dimensions (更高維多重數)。在哈密頓發展四元數的同時，將矢量拓展到高維線性空間的可能性由格拉斯曼(Hermann Gunther Grassmann，1809—1877，語言學家，數學家，物理學家)取得了進展，這體現在他1844年出版的《線性展開的學問》(Die lineale Ausdehnungslehre，Wiegand，1844)一書中(圖5)，此乃是線性代數的鼻祖！1862年，格拉斯曼還出版了《展開的學問-完備嚴謹版》(Die Ausdehnungslehre. vollst?ndig und in strenger Form begründet，Enslin，1862)一 書。然而，由于追求抽象、嚴謹，格拉斯曼的書也是只有無畏的數學家能讀，故其書出版后30年里幾乎無人問津。格拉斯曼憤而退出數學界，專心研究語言學。格拉斯曼認可數學是形式的理論，他用最一般和最抽象方式研究空間里的帶方向的線(directed lines in space)。格拉斯曼著作的目的是將幾何抽象化。注意，帶方向的線，這個形象后來被賦予給了vector一詞，甚至成了vector的標準解釋，這也是漢語矢量一詞的由來。我愿意再強調一遍，vector作為字，是攜帶者的意思，作為數學概念它可不是什么既有大小又有方向的量：vector的性質由它所遵循的線性運算法則來定義，它可以沒有方向、甚至沒有長度！此外，格拉斯曼還為我們提供了格拉斯曼代數，滿足1?ξ = ξ；ξ?ξ = 0 ，你看出來了，這可以用來描述費米子。

圖5 Grassmann和他的《作為數學新分支的展開學》(部分版本有“線性的”一詞，為線性展開學) 吉布斯在1881年出版 Elements of vector analysis 一書時是讀過格拉斯曼的著作的。吉布斯矢量分析里的某些矢量性質，并不局限于三維矢量。哈密頓，格拉斯曼和吉布斯，他們的研究都指向 multiple algebra (任意多重代數)。但是，凱萊認為多重代數始于美國人佩爾斯(Benjamin Peirce, 1809—1880，圖6)，這也是一個熱情的四元數支持者。佩爾斯1870年就寫成、在1881年正式出版了《線性結合代數》(linear associate algebra, Johns Hopkins University Press, 1881)一書，在1855年還出版過 analytical mechanics (分析力學)，可見其受哈密頓影響至深。佩爾斯認為“the greatest value of the square root of minus one was its‘ magical power of doubling the actual universe, and placing by its side an ideal universe, its exact counterpart, with which it can be comparedand contrasted, and, by means of curiously connecting fibres, form with it an organic whole, from which modern analysis has developed her surpassing geometry!’ see linear associate algebra, p.216—217”. 在《線性結合代數》這本書里，佩爾斯總結了那時的所有超復數和小于7個單位的線性結合代數。吉布斯1886年發表過名為 Multiple algebra 的文章，1887年凱萊也發表了同名文章。Erdehnungslehre, vector analysis, multiple algebra，和multiple associate algebra，這些思想匯集到一起，我們上大學時都要學的 linear algebra (線性代數)這門學問于是水到渠成。

圖6 佩爾斯

說起線性代數，必須提到矩陣一詞。線性代數的關鍵詞是 linear transformation (線性變換)，它是 multiple algebra 的根。線性矢量的變換常用一個矩陣表示。一般科學史認為矩陣一詞由凱萊于1858年提出，吉布斯認為凱萊1858年的文章 Memoir on thetheory of matrices 的基礎其實已經見于1844年格拉斯曼《展開的學問》了！實際上，1844 年，艾森斯坦 (Gotthold Eisenstein, 1823—1852) 發表的 Allgemeine Untersuchungen über die Formen dritten Grades (關于三次式的一般研究)一文也包含矩陣的思想，這是艾森斯坦于1843年夏拜會哈密頓以后發表的，而哈密頓就是被同他的談話給嚇到了，才全力以赴撿起他多次放下的triplet研究從而于當年10月16日發明了四元數的。其實，象Block of n2 quantities，代數方程組的判別式，函數變換的雅可比判別式，都容易讓人想起矩陣，或者說就是矩陣。 有趣的是，自1890年以后物理學家接受了矢量分析，作為矢量分析之母體的四元數卻被棄置道旁(有個成語買櫝還珠象是專門為此準備的)。筆者讀完十年大學都沒接觸過四元數。Sir Edmund Whittaker (1873—1956)于1940年曾呼吁復活哈密頓的四元數，當時也沒有多少響應。然而，四元數里的深刻數學與物理怎么可能會被埋沒呢？哈密頓當年就對四元數的價值深信不疑，它是關于自然的反映，它一定會帶來更多的數學與物理。我們就慢慢等著看好了。Never mind when，哈密頓1859年對泰特這樣說。其實，哪用等多久，克利福德(Willian Kingdon Clifford，1845—1879)代數的出現，作為四元數作用對象的旋量的提出，立時就讓四元數在電磁學和經典力學以外發現更神奇的應用，讓物理學家不得不認真學習四元數9)。至于由四元數開啟的發明代數對象和代數規則給數學帶去的影響，筆者不懂，不論。 05 多余的話

哈密頓第一個去掉了加在自然數之上的代數限制，打開了通往近世代數之門。去掉這些限制(交換律、分配律、結合律)的代數學的發展，讓我們更加深刻地認識了這些限制的性質。這事兒很哲學，也啟發筆者認識到太多的事物是在失去以后我們才意識到它的存在的。代數反映數的形式、結果與運算邏輯，它是自然的，必然見于物理世界。或者反過來說，欲弄明白那些描述物理的數學，認真學一下代數這門最基礎的、小學一年級就開始學的學問，可能對我們大多數人來說還是有必要的。吉布斯于1886年在 Multiple algebra 一文中寫過一句很煽情的話：“We begin by studying multiple algebra. We end, I think, by studying MULITPLE ALGEBRA!”嗯，俺們開始時學的是 multiple algebra，我們收工時發現學的是 MULITPLE ALGEBRA！若是筆者大一的時候讀過這句話，恐怕學電-動力學時也不會放任自己一腦糊涂醬吧。 面對前述電-動力學教科書里的矢量分析公式列表，筆者當時的直覺就是，這玩意兒一定不對！讓筆者傷心又欣慰的是，筆者的直覺是對的。這玩意兒到底是哪兒來的，它怎么得以流行以及其得以流行的理由是什么，它的內在缺陷和危害有哪些，我們又該如何自救？這些問題，在荒廢了許多年的大好時光以后，筆者才算有了一點點粗淺認識。筆者在此分享出來，希望能有助于未來年輕人學習物理、數學，當然也包括別的一些領域。關于知識的學習，學得淺碎不如無。可是，在不同的初期階段人們畢竟是跟從老師學習的，這老師的水平就顯得至關重要了。因此，針對老師我更想說“教人淺碎不如無”。天下之大，能糊口的職業多了去了，誤人子弟的事情并不是非干不可。一個人，若是選擇了當教師的職業，就不要指望“以其昏昏使人昭昭”的奇跡。一年級小孩的算術也許只需要教 [4 ×(3 + 2)- 6] ÷ 7 = 2 ，但老師如果修過非交換代數、非結合代數甚至非交替代數，那用前述式子教出來的小孩的前程可能就不一樣。有人可能說啦，哪能教那么多呢？我不太同意這種觀點。作為至今有了48年上學經驗的老舊小學生，我個人認為學習應該采取“牛吃草”的戰略。牛吃草，是先足足地吃一肚子再說，有空的時候通過反芻慢慢消化。知識不是線性的結構，也唯有在多知道，尤其是要多知道高深學問的框架大略，的前提下才能互相比照印證最后達成消化的效果。也許確實不可以一味追求多教，但是這不是用來掩蓋教師知識儲備嚴重不足的借口。教育的主要矛盾，永遠是學習者無限強烈的求知欲同教育者少得可憐的知識儲備之間的矛盾。

責任編輯：lq