神奇的正態分布源于“加”。
時隔多年,或許你早就記不得歲那年夏天高中悶熱的教室,但可能會記得有一天數學老師說著要給大伙看個稀奇——一塊祖傳的高爾頓板。盡管班上大多數同學都叫不出它的名字,卻也從小到大在科技館、博物館見多了,一點都提不起勁兒。老師一本正經地開始講,這個圖形就是正態分布,它有諸多的性質……午后的時光更加昏沉而緩慢地流逝。
不過,這里面蘊含的數學可一點都不無聊,讓我們來觀察一下高爾頓板的結構。
從最上方的節點往下,是幾排交錯排列的釘子。從入口扔下的小球撞上一個釘子,就像觸網的乒乓球一樣,彈向左邊和右邊的概率相等。咦?這不就是老早學過的楊輝三角嗎?最上方只有一種可能,下降之后,左右兩邊比例變成,繼續這個步驟,第行的比例系數其實就是次二項式的展開系數或者。正因如此,這種分布被稱為二項分布。
楊輝三角/圖片來源:維基百科
二項式系數看起來與正態分布風馬牛不相及,但是從高爾頓板的實驗看來,要是增加釘子的層數和底部的格子數(也就是增加),那么二項分布將逼近于正態分布:
二項分布逼近正態分布的過程丨圖片來源:維基百科
為什么一個離散的分布會跟一個連續的分布扯上關系呢?這個結論最早由法國數學家棣莫弗在1738年證明,他發現,如果不斷地拋一枚硬幣,那么得到的正面次數服從二項分布,只要拋得次數夠多,那最終將逼近正態分布。也就是說,假如賭博勝和負的概率是對半分的,那么賭博次的盈虧最終就是上面這個分布。
棣莫弗(Abraham de Moivre 1667-1754)丨圖片來源:維基百科
不過這一結論在當時并沒有引起重視,畢竟并不是所有賭徒都能像梅雷一樣交上帕斯卡這樣的朋友。百年之后,拉普拉斯試圖挽救這個定理的人氣,依然沒有成功。為了紀念這對“難兄難弟”,現在人們把這個定理稱為棣莫弗-拉普拉斯定理。
這種逼近的本質究竟是什么呢?我們看到,不管是高爾頓板,還是多次賭博,二項分布拆成每一步都是簡單的概率事件。那么就可以說,二項分布是這樣的一步一步“加”起來的。
如果是比更復雜的分布,把它們大量加起來是否仍然有類似的性質呢?高斯等人在研究實驗物理學時發現,如果對一個物理量進行多次測量,最終的測量誤差總是像這樣的:
誤差演示丨Python作圖
在物理學中,誤差來自于無關因素的微小擾動。這些擾動加起來,就是整體的誤差。這個整體誤差雖然層次不齊,但形狀與正態分布還是大致吻合的。從那以后,實驗的誤差一般都當作是正態分布。為了紀念高斯的貢獻,也把正態分布稱為高斯分布。
至此,我們已經大概能想象到,正態分布的逼近與這種“加”的性質有關,剩下證明就是數學家的事了。如今,我們把這一系列逼近正態分布的性質稱為“中心極限定理”,結論從最初的二項分布,已經擴展到了任意分布(包括同分布和不同分布)的廣闊天地。就如同上一段中的誤差——即便我們對微觀下的擾動一無所知,也能通過這種極限形式,了解大樣本下的整體行為。
應用這一思想的最為經典的例子當屬統計力學。假如有一大堆粒子,每個都雜亂無章地運動,我們自然無從知曉每一個粒子的運動狀況。不過,如果把每一個粒子的動量當作是一個隨機分布的話,那就可以把所有這些分布“加”起來當做整體的動量。如此一來,中心極限定理豈不是大有用處?
的確如此。如果對理想氣體應用中心極限定理,得到的正是大名鼎鼎的麥克斯韋速度分布:
這正是均值為,方差為的正態分布。結論并不出乎意料,畢竟速度是矢量,并沒有明顯的方向取向,所以均值是。方差的意義略微復雜一些,就此略過,不過可以直觀地理解:對于溫度越高,粒子質量越小的氣體,其速度就越不穩定。
要想得到速率(速度大小)的分布,只需要考慮速度分布這個三維空間中的一個球殼就行了。即是說,在上面那個式子基礎上乘
麥克斯韋速率分布丨圖片來源:維基百科
物理學中一般是用玻爾茲曼分布來推導麥克斯韋分布的,但玻爾茲曼分布本身也可以用中心極限定理間接推導出來。之所以說是間接,只需要看它的形式
這根本不是正態分布。歸根結底,能量的分布在這里不能相加,但在推導過程中,還是能見到正態分布。具體操作會稍微復雜一些,這里就不扯遠了。
責任編輯:lq
-
測量
+關注
關注
10文章
5161瀏覽量
112911 -
物理
+關注
關注
0文章
101瀏覽量
25273 -
系數
+關注
關注
0文章
15瀏覽量
8323
原文標題:中心極限定理:從高爾頓板到麥克斯韋分布
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
世紀大并購!傳高通有意整體收購英特爾,英特爾最新回應

FRED應用:模擬沃拉斯頓棱鏡偏振器
OCAD應用:菲涅爾透鏡初始結構設計
英特爾前Xeon首席架構師加盟高通
Kellton Tech 凱爾頓科技公司:實力背景支撐,人工智能安全的開路先鋒(創新先驅)
組合架側面端子板的結構特點
面對高通收購,Apollo 50億美元投資,你該買入英特爾股票嗎?
傳高通向英特爾發出整體收購邀約,后者市值超900億美元
高通探索收購英特爾芯片設計業務的可能性
高通或收購英特爾部分設計業務,拓展產品線戰略浮現
HDI線路板和高多層板的區別

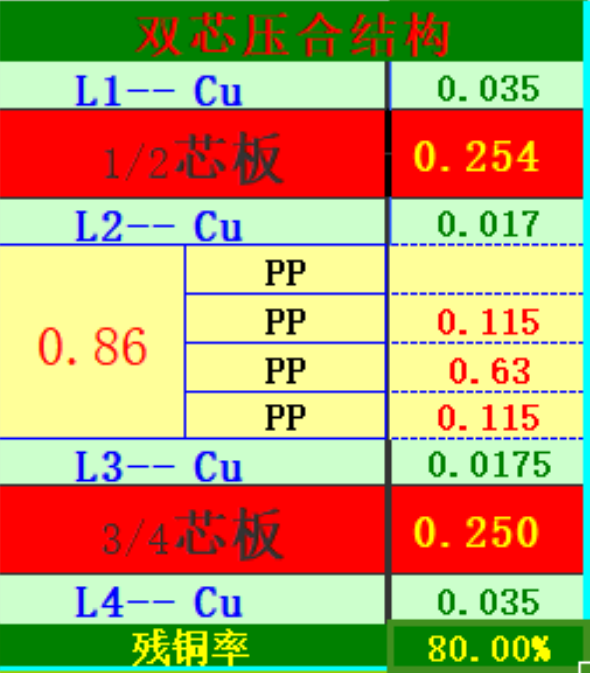
高頻PCB板 雙芯壓合結構 打包Altium Designer 14的GERBER文件


















評論