在直流電路中,功耗僅是直流電壓乘以直流電流(以瓦特為單位)的乘積。但是,對于帶有無功分量的交流電路,我們必須以不同的方式計算消耗的功率。
電功率是電路中能量消耗的“速率”,因此,所有電氣和電子組件及設備都對其可安全處理的電功率量有所限制。例如,一個1/4瓦的電阻器或一個20瓦的放大器,電力可能隨直流量或交流量而隨時間變化。電路在任何時刻的電量都稱為瞬時電量,它由功率等于伏特乘以安培(P = V * I)的眾所周知的關系給出。因此,一瓦特(每秒消耗一焦耳的能量的比率)將等于一伏特乘以一安培的伏安乘積。
那么,電路元件吸收或提供的功率就是該元件兩端的電壓V和流經(jīng)該元件的電流I的乘積。因此,如果我們有一個電阻為“ R”歐姆的直流電路,則電阻的耗散功率(以瓦特為單位)可以通過以下任一通用公式得出:
其中:V是直流電壓,I是直流電流,R是電阻值。
因此,只有當電壓和電流同時存在時,電路中的功率才存在,即沒有開路或閉路條件。考慮以下標準電阻直流電路的簡單示例:
直流電阻電路
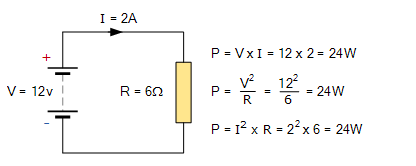
交流電路中的電力在直流電路中,電壓和電流通常是恒定的,不會隨時間變化,因為沒有與電源相關的正弦波形。但是,在交流電路中,電壓,電流和功率的瞬時值受電源的影響而不斷變化。因此,我們無法以與直流電路相同的方式來計算交流電路中的功率,但仍可以說功率(p)等于電壓(v)乘以安培(i)。
另一個重要的一點是,交流電路包含電抗,因此存在功率成分,這是由該成分產(chǎn)生的磁場和/或電場造成的。結果是,與純電阻組件不同,該功率被存儲,然后在正弦波形經(jīng)過一個完整的周期周期后返回電源。
因此,電路吸收的平均功率是一個完整周期內(nèi)存儲的功率與返回的功率之和。因此,電路的平均功耗將是一個完整周期內(nèi)瞬時功率與瞬時功率的平均值p,瞬時功率p定義為瞬時電壓v與瞬時電流i的乘積。請注意,由于正弦函數(shù)是周期性且連續(xù)的,因此在所有時間內(nèi)給出的平均功率將與在單個周期內(nèi)給出的平均功率完全相同。
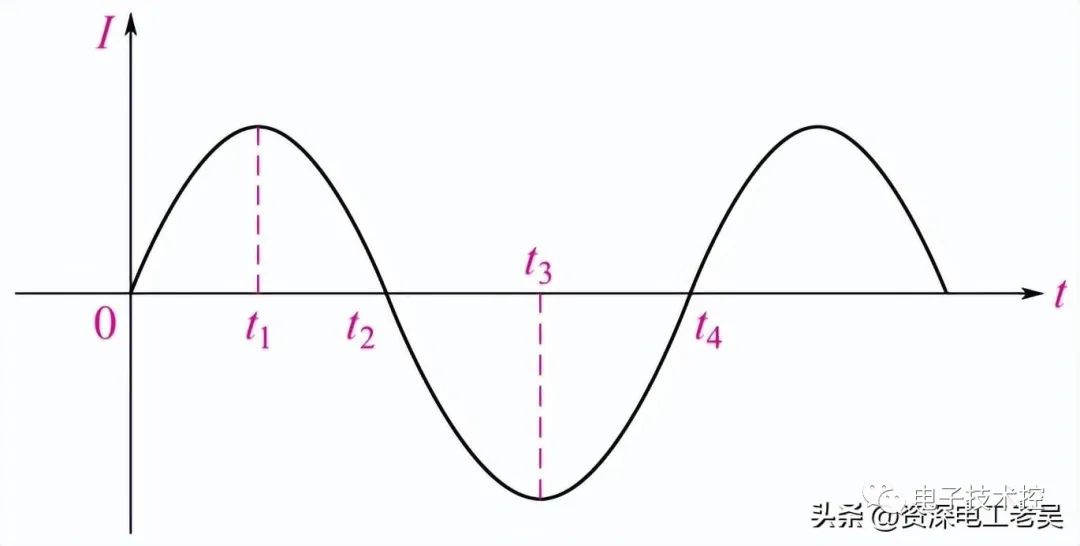
讓我們假設電壓和電流的波形都是正弦波,因此我們回想一下:
正弦電壓波形
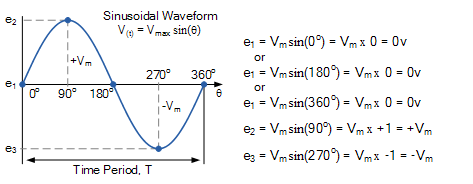
由于瞬時功率是任何時刻的功率,因此:
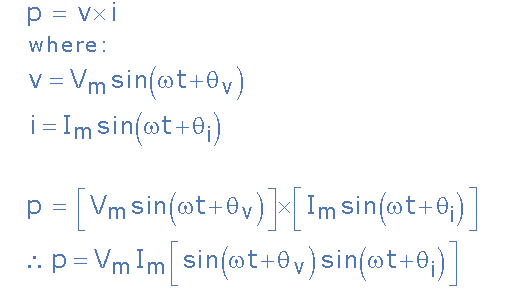
應用以下公式的三角積和和:
和θ =θ v - θ 我入上式(電壓和電流波形之間的相位差)給出:
其中V和I分別是正弦波形的均方根(rms)值,v 和i,θ是兩個波形之間的相位差。因此,我們可以將瞬時功率表示為:
瞬時交流功率方程
該方程式向我們顯示瞬時交流功率具有兩個不同的部分,因此是這兩個項的總和。第二項是隨時間變化的正弦曲線,由于項的2ω部分,其頻率等于電源角頻率的兩倍。但是,第一項是一個常數(shù),其值僅取決于電壓(V)和電流(I)之間的相位差θ。
由于瞬時功率會隨著時間的變化而正弦曲線的輪廓不斷變化,因此很難進行測量。因此,在數(shù)學上使用冪的平均值或平均值更方便,也更容易。因此,在固定的周期數(shù)內(nèi),正弦曲線瞬時功率的平均值簡單地表示為:
其中V和I是正弦有效值,而θ(Theta)是電壓和電流之間的相角。功率單位為瓦特(W)。
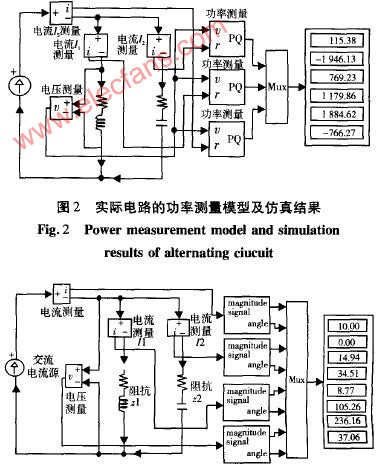
如圖所示,也可以使用流過電路的電壓V rms或電流I rms,從電路的阻抗(Z)中找到在電路中耗散的交流電源。
責任編輯人:CC
-
電源
+關注
關注
184文章
17704瀏覽量
249963 -
交流電路
+關注
關注
0文章
184瀏覽量
28836
發(fā)布評論請先 登錄
相關推薦
交流電路中電容和阻抗之間的關系,如何計算電容器的阻抗?
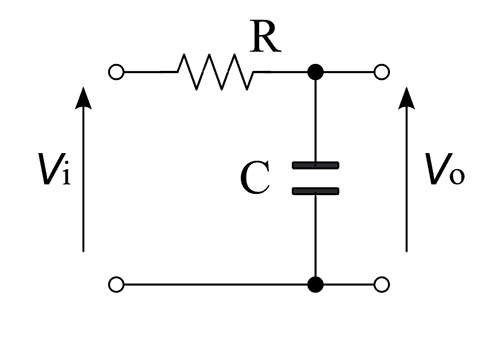
交流電路中的電源(一)
基本元件并聯(lián)的交流電路與正弦交流電路的計算舉例
正弦穩(wěn)態(tài)交流電路相量的研究
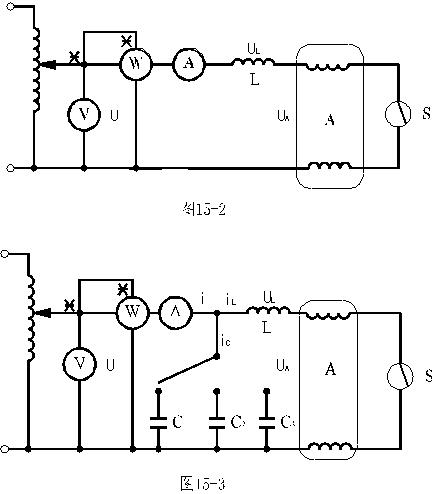
交流電路中基本參數(shù)電阻、電感和電容的測量
單項正弦交流電路的分析
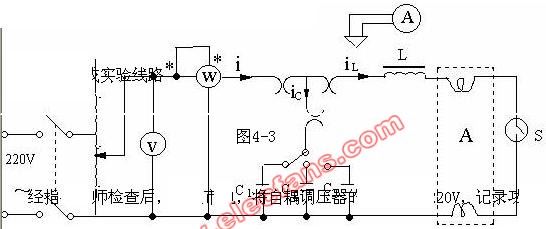
單一參數(shù)交流電路的分析計算





 一文詳解交流電路中的電源
一文詳解交流電路中的電源
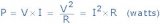










評論