讀完本文,可以去力扣解決如下題目:
215.數組中的第 K 個最大元素(Medium)
快速選擇算法是一個非常經典的算法,和快速排序算法是親兄弟。
原始題目很簡單,給你輸入一個無序的數組nums和一個正整數k,讓你計算nums中第k大的元素。
那你肯定說,給nums數組排個序,然后取第k個元素,也就是nums[k-1],不就行了嗎?
當然可以,但是排序時間復雜度是O(NlogN),其中N表示數組nums的長度。
我們就想要第k大的元素,卻給整個數組排序,有點殺雞用牛刀的感覺,所以這里就有一些小技巧了,可以把時間復雜度降低到O(NlogK)甚至是O(N),下面我們就來具體講講。
力扣第 215 題「數組中的第 K 個最大元素」就是一道類似的題目,函數簽名如下:
intfindKthLargest(int[]nums,intk);
只不過題目要求找第k個最大的元素,和我們剛才說的第k大的元素在語義上不太一樣,題目的意思相當于是把nums數組降序排列,然后返回第k個元素。
比如輸入nums = [2,1,5,4], k = 2,算法應該返回 4,因為 4 是nums中第 2 個最大的元素。
這種問題有兩種解法,一種是二叉堆(優先隊列)的解法,另一種就是標題說到的快速選擇算法(Quick Select),我們分別來看。
二叉堆解法
二叉堆的解法比較簡單,實際寫算法題的時候,推薦大家寫這種解法,先直接看代碼吧:

二叉堆(優先隊列)是比較常見的數據結構,可以認為它會自動排序,我們前文 手把手實現二叉堆數據結構 實現過這種結構,我就默認大家熟悉它的特性了。
看代碼應該不難理解,可以把小頂堆pq理解成一個篩子,較大的元素會沉淀下去,較小的元素會浮上來;當堆大小超過k的時候,我們就刪掉堆頂的元素,因為這些元素比較小,而我們想要的是前k個最大元素嘛。當nums中的所有元素都過了一遍之后,篩子里面留下的就是最大的k個元素,而堆頂元素是堆中最小的元素,也就是「第k個最大的元素」。
二叉堆插入和刪除的時間復雜度和堆中的元素個數有關,在這里我們堆的大小不會超過k,所以插入和刪除元素的復雜度是O(logK),再套一層 for 循環,總的時間復雜度就是O(NlogK)。空間復雜度很顯然就是二叉堆的大小,為O(K)。
這個解法算是比較簡單的吧,代碼少也不容易出錯,所以說如果筆試面試中出現類似的問題,建議用這種解法。唯一注意的是,Java 的PriorityQueue默認實現是小頂堆,有的語言的優先隊列可能默認是大頂堆,可能需要做一些調整。
快速選擇算法
快速選擇算法比較巧妙,時間復雜度更低,是快速排序的簡化版,一定要熟悉思路。
我們先從快速排序講起。
快速排序的邏輯是,若要對nums[lo..hi]進行排序,我們先找一個分界點p,通過交換元素使得nums[lo..p-1]都小于等于nums[p],且nums[p+1..hi]都大于nums[p],然后遞歸地去nums[lo..p-1]和nums[p+1..hi]中尋找新的分界點,最后整個數組就被排序了。
快速排序的代碼如下:

關鍵就在于這個分界點索引p的確定,我們畫個圖看下partition函數有什么功效:
索引p左側的元素都比nums[p]小,右側的元素都比nums[p]大,意味著這個元素已經放到了正確的位置上,回顧快速排序的邏輯,遞歸調用會把nums[p]之外的元素也都放到正確的位置上,從而實現整個數組排序,這就是快速排序的核心邏輯。
那么這個partition函數如何實現的呢?看下代碼:
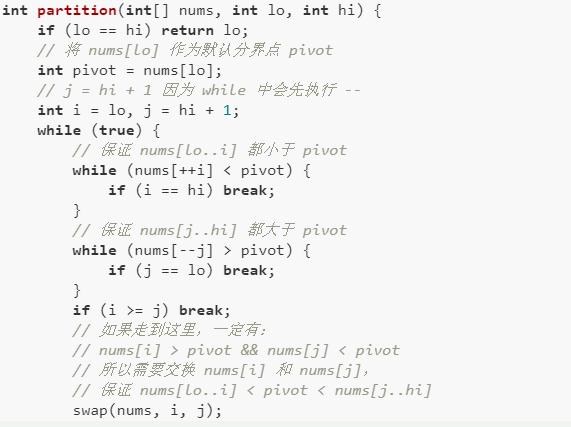

熟悉快速排序邏輯的讀者應該可以理解這段代碼的含義了,這個partition函數細節較多,上述代碼參考《算法4》,是眾多寫法中最漂亮簡潔的一種,所以建議背住,這里就不展開解釋了。
好了,對于快速排序的探討到此結束,我們回到一開始的問題,尋找第k大的元素,和快速排序有什么關系?
注意這段代碼:
intp=partition(nums,lo,hi);
我們剛說了,partition函數會將nums[p]排到正確的位置,使得nums[lo..p-1] < nums[p] < nums[p+1..hi]。
那么我們可以把p和k進行比較,如果p < k說明第k大的元素在nums[p+1..hi]中,如果p > k說明第k大的元素在nums[lo..p-1]中。
所以我們可以復用partition函數來實現這道題目,不過在這之前還是要做一下索引轉化:
題目要求的是「第k個最大元素」,這個元素其實就是nums升序排序后「索引」為len(nums) - k的這個元素。
這樣就可以寫出解法代碼:

這個代碼框架其實非常像我們前文二分搜索框架的代碼,這也是這個算法高效的原因,但是時間復雜度為什么是O(N)呢?按理說類似二分搜索的邏輯,時間復雜度應該一定會出現對數才對呀?
其實這個O(N)的時間復雜度是個均攤復雜度,因為我們的partition函數中需要利用雙指針技巧遍歷nums[lo..hi],那么總共遍歷了多少元素呢?
最好情況下,每次p都恰好是正中間(lo + hi) / 2,那么遍歷的元素總數就是:
N + N/2 + N/4 + N/8 + … + 1
這就是等比數列求和公式嘛,求個極限就等于2N,所以遍歷元素個數為2N,時間復雜度為O(N)。
但我們其實不能保證每次p都是正中間的索引的,最壞情況下p一直都是lo + 1或者一直都是hi - 1,遍歷的元素總數就是:
N + (N - 1) + (N - 2) + … + 1
這就是個等差數列求和,時間復雜度會退化到O(N^2),為了盡可能防止極端情況發生,我們需要在算法開始的時候對nums數組來一次隨機打亂:

前文洗牌算法詳解寫過隨機亂置算法,這里就不展開了。當你加上這段代碼之后,平均時間復雜度就是O(N)了,提交代碼后運行速度大幅提升。
總結一下,快速選擇算法就是快速排序的簡化版,復用了partition函數,快速定位第 k 大的元素。相當于對數組部分排序而不需要完全排序,從而提高算法效率,將平均時間復雜度降到O(N)。
責任編輯:xj
原文標題:快排親兄弟:快速選擇算法詳解
文章出處:【微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
-
算法
+關注
關注
23文章
4608瀏覽量
92844 -
代碼
+關注
關注
30文章
4780瀏覽量
68539
原文標題:快排親兄弟:快速選擇算法詳解
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 215.數組中的第K個最大元素(Medium)
215.數組中的第K個最大元素(Medium)










評論