移動通信技術對數據傳輸速率要求越來越高。一種提高傳輸速率的思路是使用更高階的QAM 調制方式,例如5G NR 的256QAM PDSCH,微波的1024QAM,2048QAM和4096QAM 調制。更高階的QAM 調制方式對系統也提出了更高的要求。例如某個系統的EVM 測試結果為3%,這個EVM 算好還是不好,單純從數值看似乎很好,但是EVM 的好壞與否不僅要看數值,還要看其調制階數,不同調制階數對EVM要求不同。直觀來看,更高階QAM 調制方式對EVM 有更高要求,但是具體要求是多少?例如對1024QAM 調制,EVM 要小于多少才能實現正常通信?本文主要討論這個問題。EVM確定了,就可以指導系統信噪比SNR(SIGNAL NOISE RATIO)的指標分解和預算。
例如3GPP TS38.141對5G NR 不同調制方式的PDSCH EVM 要求如下表,從表中也可以看到隨著調制階數的提高,EVM 的要求在不斷提高,這些EVM 是怎么定出來的?目前已經有客戶開始測試1024QAM 的PDSCH,TS38.141 沒有給出1024QAM 的EVM 要求,在測試的時候1024QAM EVM多少才算通過?本文將會給出答案。
表1、TS38.141對不同階QAM EVM指標要求
| Modulation scheme for PDSCH | Required EVM (%) |
| QPSK | 18.50% |
| 16QAM | 13.50% |
| 64QAM | 9% |
| 256QAM | 4.50% |
1、QAM調制及EVM以及EVM與SNR的關系
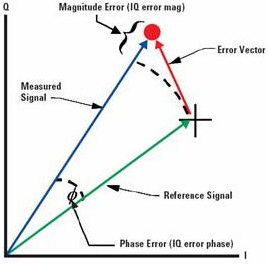
圖1、EVM定義
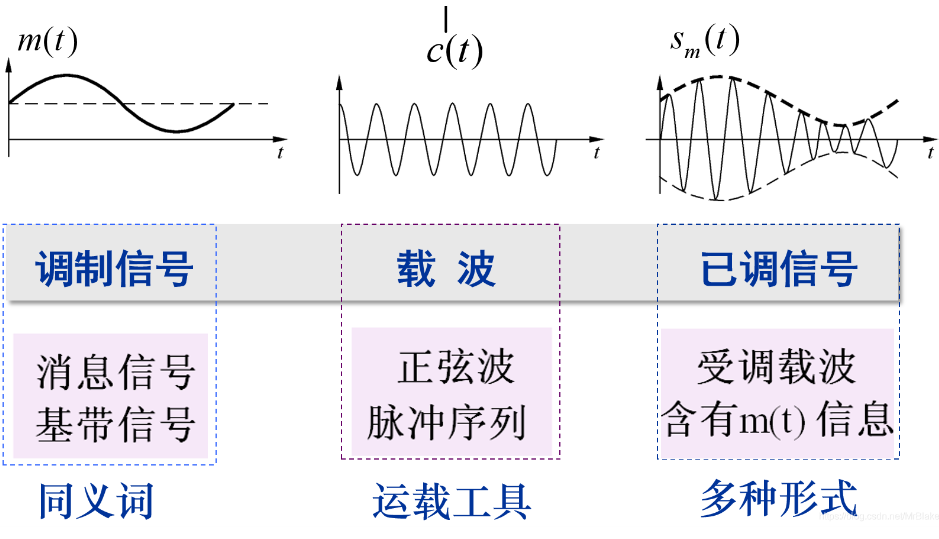
QAM 調制信號通常用其EVM 來衡量信號質量,EVM是英文Error Vector Magnitude縮寫,意為誤差向量幅度,其定義為誤差矢量Error Vector 的幅度與參考信號Reference Signal 幅度的比值,有時候用百分比比表示,有時候用dB 表示。通常測量的EVM為其RMS 值,計算公式如下:
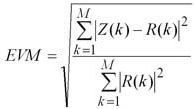
EVM 可以與信噪比SNR 相互換算,在星座圖中,EVM 是以電壓表示的,因而二者之間的換算公式如下,當然如果有編碼增益,要在該公式中考慮編碼增益,例如擴頻增益。
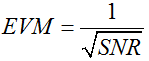
2、不同階QAM信號對EVM的要求
不同階QAM 對信號的抗干擾能力是不一樣的,數字調制信號調制方式越復雜,頻率帶寬利用率越高,調制方式越復雜,抗干擾能力越差,功率利用率低,也就是說接收時需要較高的C/N比,才能達到相同傳輸質量,選擇調制方式需要根據通信系統在這兩個方面折衷256QAM 的符號點間距離比BPSK 調制近的多,這意味256QAM 和BPSK 相比容易被干擾而造成誤碼。
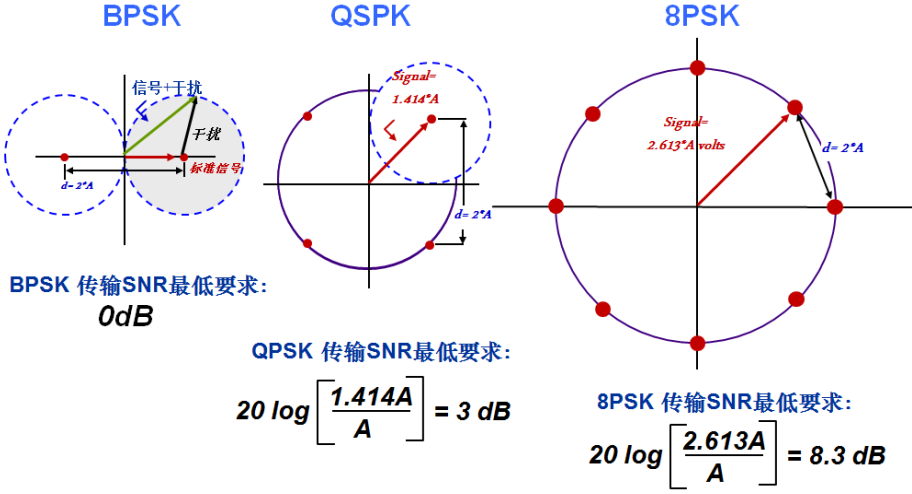
圖2、不同調制方式抗干擾能力
從EVM 的含義看,結合幾種調制方式的星座圖拿來看,如果要保證通信正常,也就是星座點不發生誤判,則要求每個星座點的誤差矢量幅度最大為0.5a(其中a 為相鄰星座點之間的間距),即|E|max<0.5a,因而每個星座點需要落在以參考信號為中心,半徑為0.5a 的圓內。由于不同星座點的參考信號幅度是不一樣的,離原點最遠的那個星座點對應的參考信號幅度最大,記為|R|max,則其可容忍的EVM 最小,即EVM_thre=0.5a/|R|max,只要所有星座點的EVM小于EVM_thre,就不會發生誤判,即總的EVM 小于EVM_thre。下圖中的A=0.5a,表示相鄰星座點間距的一半。
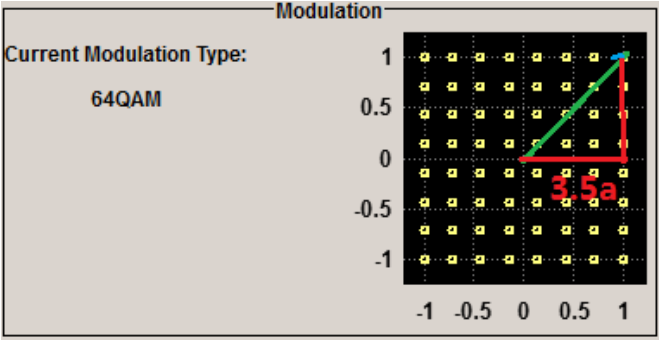
圖3、64QAM EVM_thre 示意圖
比如64QAM,星座圖可以看作是間距為a 的8x8 陣列,那么距離原點最遠的那個星座點坐標就是(3.5a,3.5a),矢量長度為1.414x3.5a,為了不發生誤判,允許的矢量誤差要小于半個星座間距(0.5a),這時的EVM<0.5a/(1.414x3.5a)=10.10%,為了保證接收機正常解調,留有一定的余量,5G NR 協議TS38.141 將64QAM 的EVM 限值設定在9%,是合理的。
當然這種估算方法保證了所有星座點的都不會發生誤判,由于距離原點近一點的星座點參考信號幅度會小些,其EVM 會大些也不會發生誤判,假設所有星座點同時達到最大誤差矢量|E|max=0.5a,同時所有星座點等概率出現,此時系統的EVM 達到容忍上限,EVM 再大就會誤判。此時系統的EVM RMS 值成為EVMRMS_thre,只要EVM 小于改值EVMRMS_thre,則系統一定不會發生誤判。

圖4、計算不同QAM 調制方式下對系統EVM 和SNR 要求門限
通過圖4 Matlab 代碼就可以計算出EVMRMS_thre 和EVM_thre,并計算出了其對系統SNR 的要求值。不同調制方式下對系統要求的EVM 和SNR 門限如表2 所示。從表中可看出,調制階數越高,對系統的EVM 和SNR 要求就越高。
表2、不同QAM 調制方式對系統EVM 和SNR 要求
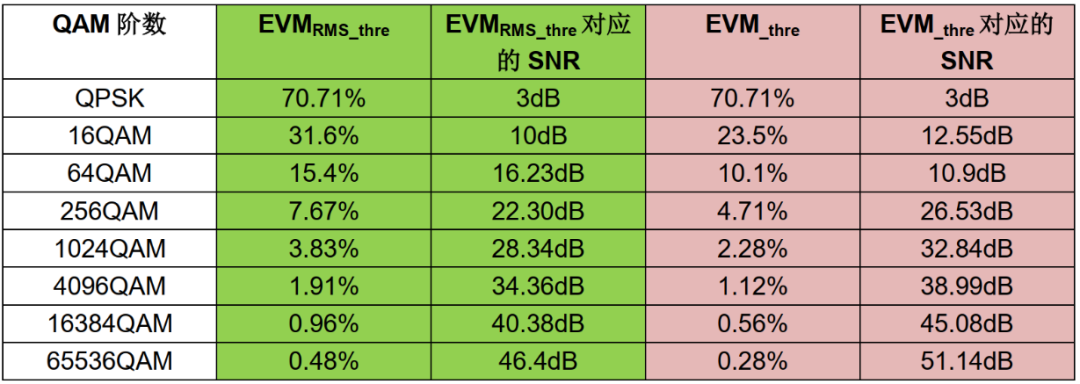
以目前已經使用的最高調制階數4096QAM 為例,其對系統的EVM 的RMS值要求小于1.91%,如果以最遠點計算EVM 要求小于1.12%。如果將信號源和頻譜儀直接相連,相當于在沒有衰落的靜態信道條件下,EVM RMS 值最好一般在0.2%左右,所以4096QAM 對EVM 的要求已經接近于硬件的極限水平。
3、實驗驗證
使用信號源產生一個4096QAM 信號,使用頻譜分析儀進行解調。
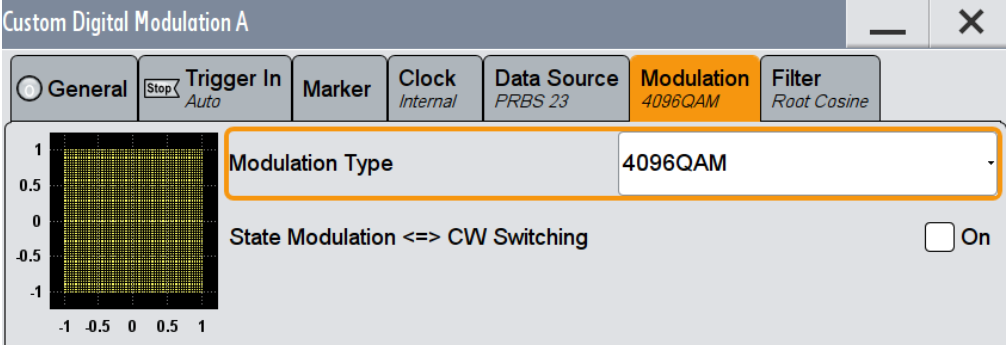
圖5、生成4096QAM 調制信號
在不額外增加噪聲的條件下,FSW 的解調結果如圖6,其EVM 很好,星座圖清晰可見。
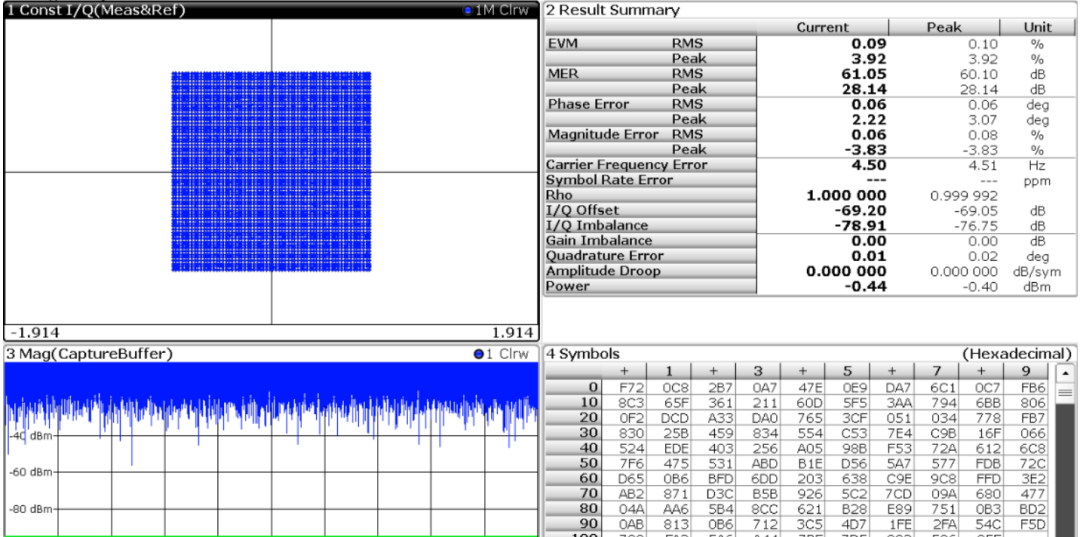
圖6、不加噪聲下FSW 對4096QAM 信號解調結果
根據表1 計算結果,4096QAM 對系統的EVM 要求必須小于1.91%,對應的SNR 為34.36dB。在上述信號基礎上增加-34dB 的AWGN 噪聲,此時加噪聲后信號的解調結果如圖8 所示,星座圖已經接近于模糊和誤判,對應的EVM 測試結果為1.56%,與理論計算1.91%還是比較接近。
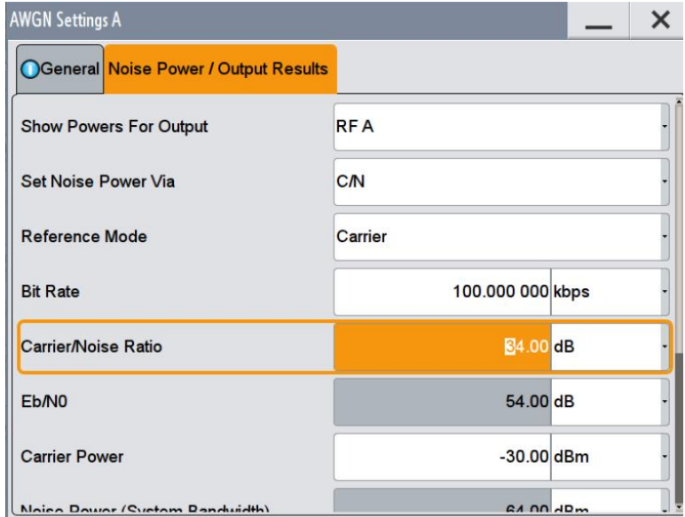
圖7、4096QAM 信號增加-34dB 的AWGN 噪聲
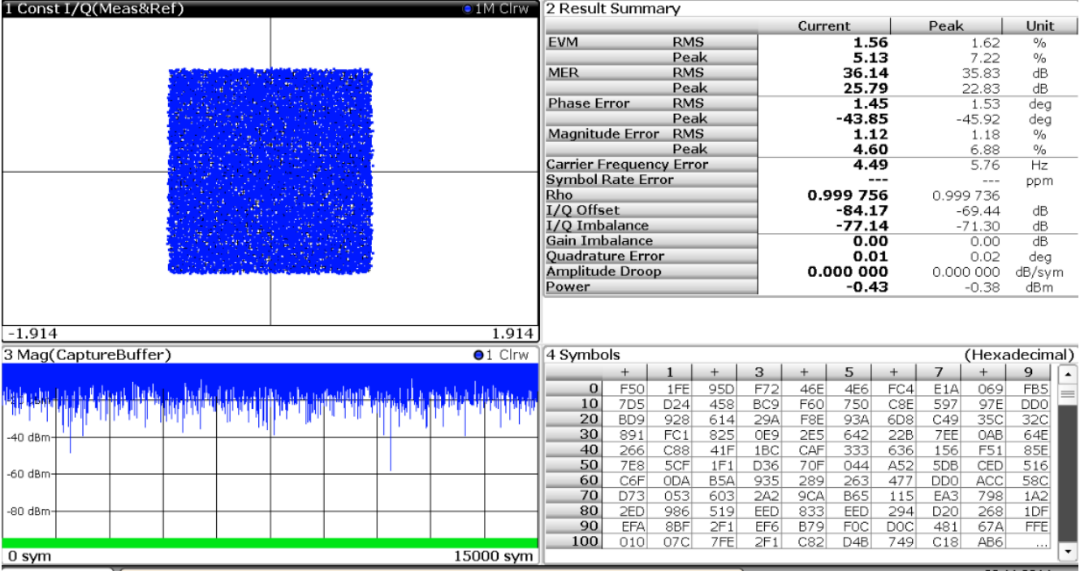
圖8、加-34dB 噪聲下FSW 對4096QAM 信號解調結果
4、結論
更高階的QAM 調制方式對系統EVM 和SNR 提出了更高的要求,系統的EVM 測試結果算好還是不好,不能只單純看EVM 數值,還要看其調制階數。本文計算了不同調制階數下星座點不發生誤判時對系統的EVM 和SNR 要求,具體結果參考表2,該結論可以理解調制階數與EVM的關系以及對系統SNR的要求,可以用來指導系統設計和器件選型。
原文標題:5G NR調制階數與EVM關系以及對系統SNR要求分析
文章出處:【微信公眾號:微波射頻網】歡迎添加關注!文章轉載請注明出處。
責任編輯:haq
-
通信
+關注
關注
18文章
6024瀏覽量
135950 -
SNR
+關注
關注
3文章
195瀏覽量
24405 -
EVM
+關注
關注
3文章
866瀏覽量
41041 -
5G
+關注
關注
1354文章
48436瀏覽量
563965
原文標題:5G NR調制階數與EVM關系以及對系統SNR要求分析
文章出處:【微信號:mwrfnet,微信公眾號:微波射頻網】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
AFE7071 RF輸出0.5*LO and 1.5*LO frequency處有異常噪聲怎么解決?
PGA308的evm板通迅正常,為什么沒有電壓輸出?
什么是正交幅度調制(QAM)?
中國聯通超大帶寬和1024QAM商用驗證完成,單用戶速率達5.52G
三星與高通聯手實現1024QAM,下行速度提升超20%?
QPSK調制解調機制深入解析




 1024QAM調制中EVM要小于多少才能正常通信?
1024QAM調制中EVM要小于多少才能正常通信?










評論