作者:Divyanshu Mishra
編譯:ronghuaiyang
導讀
權值衰減和L2正則化,到底是不是同一個東西,這篇文章給你答案。
神經網絡是偉大的函數逼近器和特征提取器,但有時它們的權值變得過于特定化,導致過擬合。這就是正則化概念出現的地方,我們將討論兩種主要權重正則化技術之間的細微差別,它們經常被錯誤地認為是相同的。
介紹
1943年,Warren McCulloch和Walter Pitts首先提出了神經網絡,但當時還不夠流行,因為神經網絡需要大量數據和計算能力,這在當時是不可行的。但隨著上述約束條件和其他訓練技術的進步(如參數初始化和更好的激活函數)變得可行,它們再次開始主導各種比賽,并在各種人類輔助技術中找到了它的應用。
如今,神經網絡構成了許多著名應用的最主要的部分,如自動駕駛汽車、谷歌翻譯、人臉識別系統等,并應用于幾乎所有人類發展所使用的技術。
神經網絡非常擅長于將函數近似為線性或非線性,在從輸入數據中提取特征時也非常出色。這種能力使他們在大量的任務中表現出色,無論是計算機視覺領域還是語言建模。但我們都聽過這句名言:
“能力越大,責任越大。”
這句話也適用于全能的神經網絡。它們作為強大的函數近似器的能力有時會導致它們通過逼近一個函數來過擬合數據集,這個函數在它被訓練過的數據上表現得非常好,但在測試它之前從未見過的數據時卻敗得很慘。更有技術意義的是,神經網絡學習的權值對給定的數據更加專門化,而不能學習可以一般化的特征。為了解決過擬合的問題,應用了一類稱為正則化的技術來降低模型的復雜性和約束權值,迫使神經網絡學習可泛化的特征。
正則化
正則化可以定義為我們為了減少泛化誤差而不是減少訓練誤差而對訓練算法所做的任何改變。有許多正規化策略。有的對模型添加額外的約束,如對參數值添加約束,有的對目標函數添加額外的項,可以認為是對參數值添加間接或軟約束。如果我們仔細使用這些技術,這可以改善測試集的性能。在深度學習的環境中,大多數正則化技術都基于正則化估計器。當正則化一個估計量時,有一個折衷,我們必須選擇一個增加偏差和減少方差的模型。一個有效的正規化是使一個有利可圖的交易,顯著減少方差,而不過度增加偏差。
在實踐中使用的主要正規化技術有:
① L2正則化
② L1正則化
③ 數據增強
④ Dropout
⑤ Early Stopping
在這篇文章中,我們主要關注L2正則化,并討論我們是否可以將L2正則化和權重衰減作為同一枚硬幣的兩面。
L2 正則化
L2正則化屬于正則化技術的一類,稱為參數范數懲罰。之所以提到這類技術,是因為在這類技術中,特定參數的范數(主要是權重)被添加到被優化的目標函數中。在L2范數中,在網絡的損失函數中加入一個額外的項,通常稱為正則化項。例如:
交叉熵損失函數的定義如下所示。
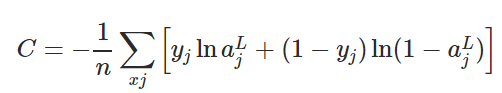

為了將L2正則化應用于任何有交叉熵損失的網絡,我們將正則化項添加到損失函數中,其中正則化項如下所示:

在上式中,λ是正則化參數,與應用的正則化量成正比。如果λ=0,則不應用正則化,當λ= 1時,對網絡應用最大正則化。λ是一個超參數,這意味著它不是在訓練期間學習的,而是由用戶手動調整或使用一些超參數調整技術,如隨機搜索。
現在讓我們把這些放在一起,形成L2正則化的最終方程,應用于下式所給出的交叉熵損失函數。

上面的例子展示了L2正則化應用于交叉熵損失函數,但這一概念可以推廣到所有可用的損失函數。下式給出了L2正則化更一般的公式,其中C0為非正則化損失函數,C為加入正則化項的正則化損失函數。

注:我們在對網絡進行正則化時不考慮網絡的bias,原因如下:
1、與權重相比,bias通常需要更少的數據來精確擬合。每個權重指定了兩個變量如何相互作用(w和x),因此要想很好地擬合權重,就需要在各種條件下觀察兩個變量,而每個bias只控制一個單一變量(b)。因此,我們對bias不使用正則化,以免引入太多的方差。2、對bias進行正則化可能引入大量的欠擬合。
為什么L2 正則化有用?
實踐推理:
讓我們試著理解L2正則化基于損失函數的梯度的工作原理。如果我們對網絡中所有權重和偏差取上面式子中所示方程的偏導數或梯度,即?C/?w和?C/?b。求偏導數,我們得到:

我們可以使用backpropagation算法計算上述方程中提到的?C0/?w和?C0/?b項。由于沒有應用正則化項,偏置參數的偏導將不變,而權重參數將包含額外的(λ/n)*w)正則化項。
偏置和權重的學習規則由此變為:
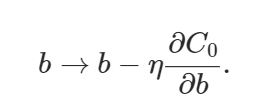
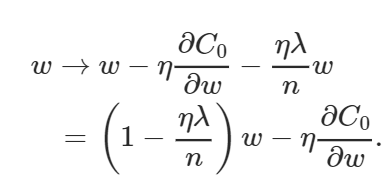
上面的權值方程類似于通常的梯度下降學習規則,除了現在我們首先通過 (1?(η*λ)/n)重新調整權值w。這就是L2正則化經常被稱為權重衰減的原因,因為它使權重變小。因此,你可以看到為什么正則化工作的時候,它使網絡的權值更小。權值變小意味著,如果我們在這里或那里改變一些隨機輸入,網絡的行為不會有太大的變化,這反過來使正則化的網絡很難學習數據中的局部噪聲。這迫使網絡只學習那些在訓練集中經常看到的特征。
個人的直覺:
簡單地從優化損失函數的角度來考慮L2正則化,當我們把正則化項添加到損失函數中我們實際上增加了損失函數的值。因此,如果權值越大,損失也就越高,訓練算法會試圖通過懲罰權值來降低損失函數,迫使它們取更小的值,從而使網絡正則化。
L2 正則化和權值衰減是一樣的嗎?
L2正則化和權值衰減并不是一回事,但是可以根據學習率對權值衰減因子進行重新參數化,從而使SGD等價。不明白?讓我給你詳細解釋一下。
以λ為衰減因子,給出了權值衰減方程。

在以下證明中可以證明L2正則化等價于SGD情況下的權值衰減:
1、讓我們首先考慮下面圖中給出的L2正則化方程。我們的目標是對它進行重新參數化,使其等價于上式中給出的權值衰減方程。
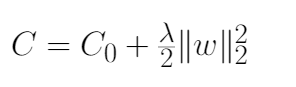
2、首先,我們找到L2正則化損失函數相對于參數w的偏導數(梯度),如下式所示。


注意:上圖中這兩種符號的意思是一樣的。
3、得到損失函數的偏導數結果后,將結果代入梯度下降學習規則中,如下式所示。代入后,打開括號,重新排列,使其等價于在一定假設下的權值衰減方程。

4、你可以注意到,最終重新排列的L2正則化方程和權值衰減方程之間的唯一區別是α(學習率)乘以λ(正則化項)。為了得到兩個方程,我們用λ來重新參數化L2正則化方程。
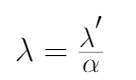
5、將λ'替換為λ,對L2正則化方程進行重新參數化,將其等價于權值衰減方程,如下式所示。

從上面的證明中,你必須理解為什么L2正則化在SGD情況下被認為等同于權值衰減,但對于其他基于自適應梯度的優化算法,如Adam, AdaGrad等,卻不是這樣。特別是,當與自適應梯度相結合時,L2正則化導致具有較大歷史參數和/或梯度振幅的權值比使用權值衰減時正則化得更少。這導致與SGD相比,當使用L2正則化時adam表現不佳。另一方面,權值衰減在SGD和Adam身上表現得一樣好。
一個令人震驚的結果是,帶有動量的SGD優于像Adam這樣的自適應梯度方法,因為常見的深度學習庫實現了L2正則化,而不是原始的權重衰減。因此,在使用L2正則化有利于SGD的任務上,Adam的結果要比使用動量的SGD差。
總結
因此,我們得出結論,盡管權值衰減和L2正則化在某些條件下可以達到等價,但概念上還是有細微的不同,應該區別對待,否則可能導致無法解釋的性能下降或其他實際問題。
本文轉自:AI公園,作者:Divyanshu Mishra,編譯:ronghuaiyang,
轉載此文目的在于傳遞更多信息,版權歸原作者所有。
審核編輯 黃昊宇
-
神經網絡
+關注
關注
42文章
4771瀏覽量
100723 -
正則化
+關注
關注
0文章
17瀏覽量
8128
發布評論請先 登錄
相關推薦
ADS131M03打印輸出的電壓值與實際輸入電壓值對不上是怎么回事?
模擬信號、數字信號、ADC與DAC傻傻分不清楚?一文了解,收藏再看

用adc讀取電壓值時,顯示的電壓值是亂碼怎么解決?
PLC多種通訊方式匯總學習~

用adc讀取電壓值時,顯示的電壓值是亂碼,如何解決?
如果在不清楚適配器的是否支持QC3.0的情況下,嘗試切換至QC3.0協議,該如何判斷是否成功切換至QC3.0協議?
頻段、信道、帶寬和傳輸速率,還傻傻分不清楚?

LDO和DCDC還傻傻分不清?快來搞懂它

一文介紹:UWB-AOA產品特點及其應用
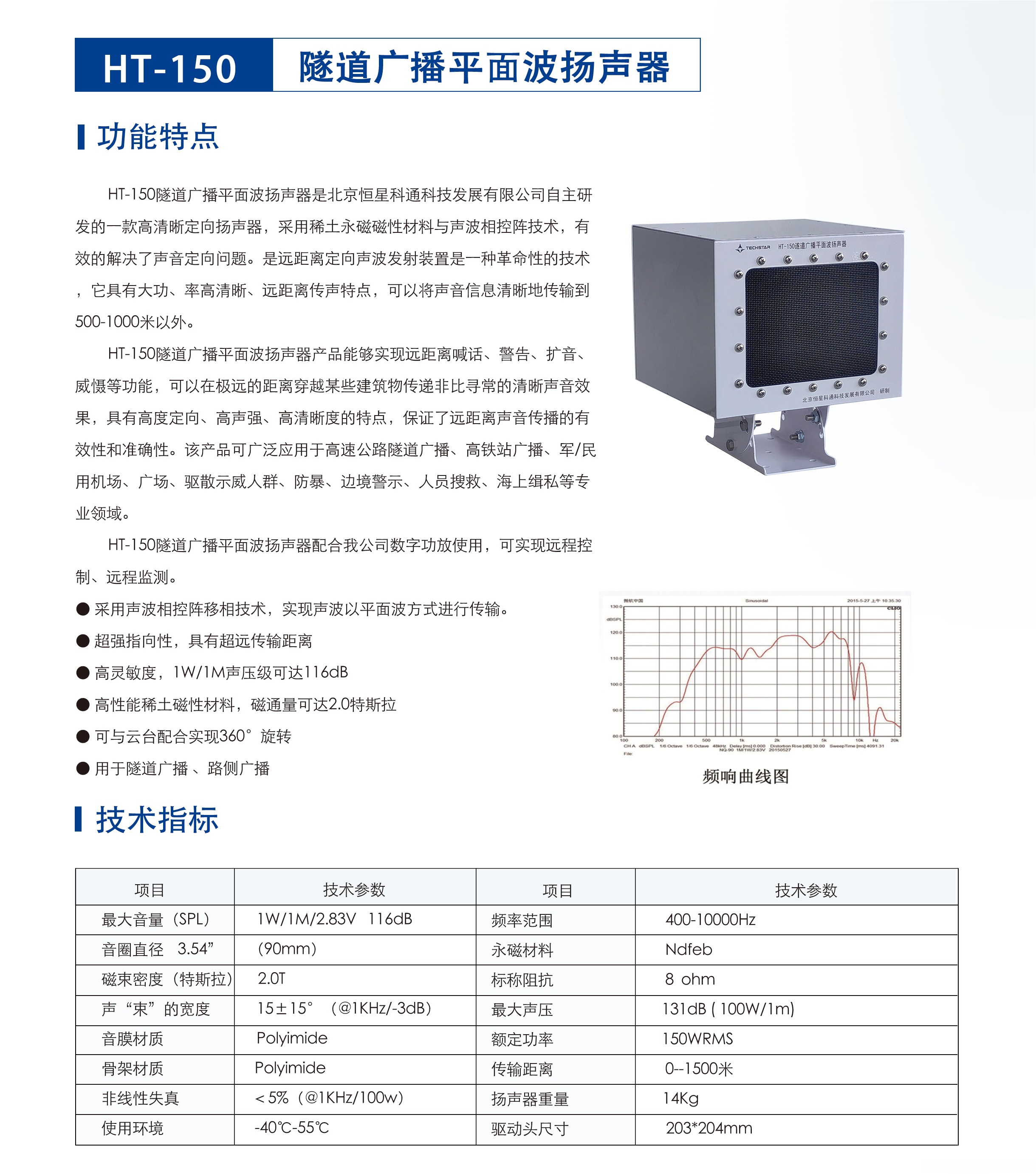
如何解決隧道廣播聽不清楚的問題
傻傻分不清?射頻模擬信號源和矢量信號源的區別
晶體與晶振傻傻分不清?看完這篇文章您就明白了

晶體與晶振傻傻分不清?看完這篇文章您就明白了





 權值衰減和L2正則化傻傻分不清楚?本文來教會你如何分清
權值衰減和L2正則化傻傻分不清楚?本文來教會你如何分清










評論