袁廚攜袁記菜館全體工作人員祝大家在新的一年,健健康康,開開心心。發量暴增,錢包超大。
哎,元旦假期結束了,又要繼續搬磚了,我們接著做題吧,今天我們好好說說單調棧和單調隊列。其實很容易理解,單調棧就是棧內單調遞增或單調遞減的棧,棧內元素是有序的,單調隊列同樣也是。
下面我們通過幾個題目由淺入深,一點一點挖透他們吧!
提綱
單調隊列
劍指 Offer 59 - II. 隊列的最大值
題目描述:
請定義一個隊列并實現函數 max_value 得到隊列里的最大值
若隊列為空,pop_front 和 max_value 需要返回 -1
示例 1:
輸入: ["MaxQueue","push_back","push_back","max_value","pop_front","max_value"]
[[],[1],[2],[],[],[]]
輸出: [null,null,null,2,1,2]
示例 2:
輸入:
["MaxQueue","pop_front","max_value"]
[[],[],[]]
輸出: [null,-1,-1]
題目解析:
我們先來拆解下上面的示例 1

其實我覺得這個題目的重點在理解題意上面,可能剛開始刷題的同學,對題意理解不夠透徹,做起來沒有那么得心應手,通過上面的圖片我們簡單了解了一下題意,那我們應該怎么做才能實現上述要求呢?
下面我們來說一下雙端隊列。我們之前說過的隊列,遵守先進先出的規則,雙端隊列則可以從隊頭出隊,也可以從隊尾出隊,不用遵守先進先出的規則,我們先通過一個視頻來簡單了解下雙端隊列。
我們可以用雙端隊列做輔助隊列,用輔助隊列來保存當前隊列的最大值。我們同時定義一個普通隊列和一個雙端單調隊列。普通隊列就正常執行入隊,出隊操作。max_value 操作則返回咱們的雙端隊列的隊頭即可。下面我們來看一下代碼的具體執行過程吧。
我們來對視頻進行解析
1.我們需要維護一個單調雙端隊列,上面的隊列則執行正常操作,下面的隊列隊頭元素則為上面隊列的最大值
2.出隊時,我們需要進行對比兩個隊列的隊頭元素是否相等,如果相等則同時出隊,則出隊后的雙端隊列的頭部仍為上面隊列中的最大值。
3.入隊時,我們需要維持一個單調遞減的雙端隊列,因為我們需要確保隊頭元素為最大值嘛。
題目代碼:

239.滑動窗口最大值
題目描述:
給你一個整數數組 nums,有一個大小為 k 的滑動窗口從數組的最左側移動到數組的最右側。你只可以看到在滑動窗口內的 k 個數字。滑動窗口每次只向右移動一位。
返回滑動窗口中的最大值。
示例1:
輸入:nums = [1,3,-1,-3,5,3,6,7], k = 3 輸出:[3,3,5,5,6,7]
題目解析:
題目讓我們找出每個滑動窗口的最大值,那么題目具體含義是怎樣呢?

就是為了讓我們輸出每個窗口的最大值,那我們思考一下,我們一個數組一共有多少窗口呢?
比如我們這個例子中,我們的窗口長度為 3 ,數組長度為 8,我們的窗口每次移動一位,所以我們一共有 8 - (3 - 1)也就是 8 - 3 + 1。所以我們返回數組的長度是跟原數組長度和滑動窗口的長度有關的。
也就是 winlen = len(數組長度) - k(滑動窗口長度) + 1。下面我們來看一個視頻,相信通過這個視頻,大家一下就能搞懂啦。
下面我們對視頻進行拆解。
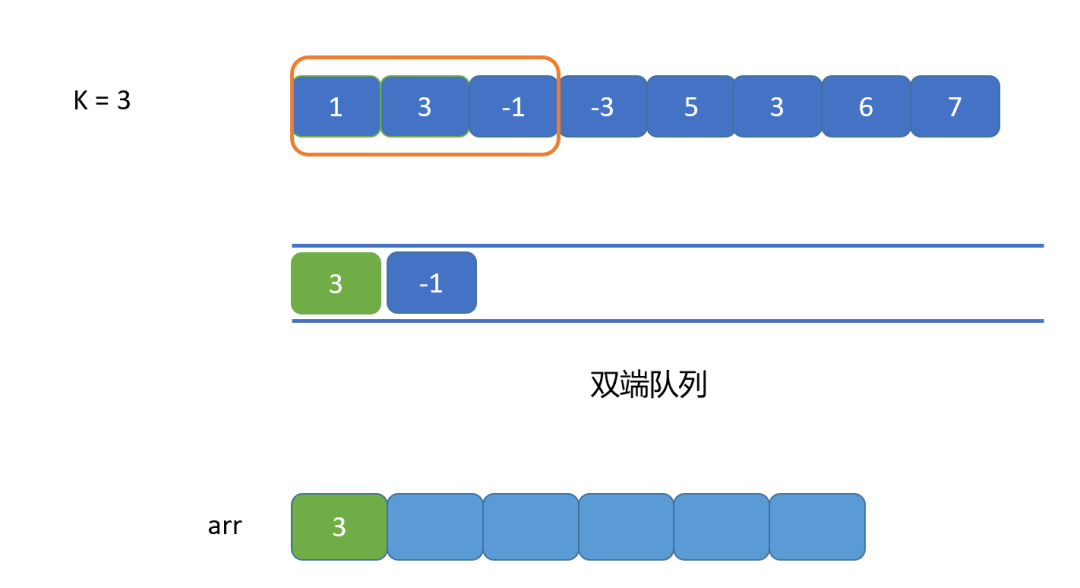
1.先將我們第一個窗口的所有值按照規則存入單調雙端隊列中,單調隊列里面的值為單調遞減的。如果發現隊尾元素小于要加入的元素,則將隊尾元素出隊,直到隊尾元素大于等于新元素時,再讓新元素入隊,目的就是維護一個單調遞減的隊列。第一個窗口的所有值入隊之后情況,如下圖。是因為 3 要入隊時,此時隊中有 1 ,不能保證單調遞減,所以需要 1 出隊,然后 3 入隊, -1 入隊時,隊中有 3 ,滿足單調,所以 -1 可以入隊。

2.我們將第一個窗口的所有值,按照單調隊列的規則入隊之后,因為隊列為單調遞減,所以隊頭元素必為當前窗口的最大值,則將隊頭元素添加到數組中。
3.移動窗口,判斷當前窗口前的元素是否和雙端隊列隊頭元素相等,如果相等則出隊,此時滑動窗口的最大值發生改變了。
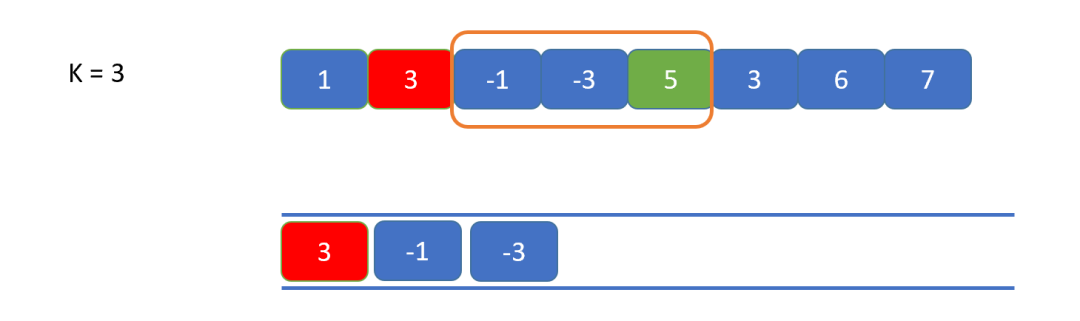
4.繼續然后按照規則進行入隊,維護單調遞減隊列,這里和第一條規則一致。
5.每次將隊頭元素存到返回數組里。
6.返回數組
是不是一下就搞懂啦。你真帥,下面我們來看一下代碼吧。
題目代碼
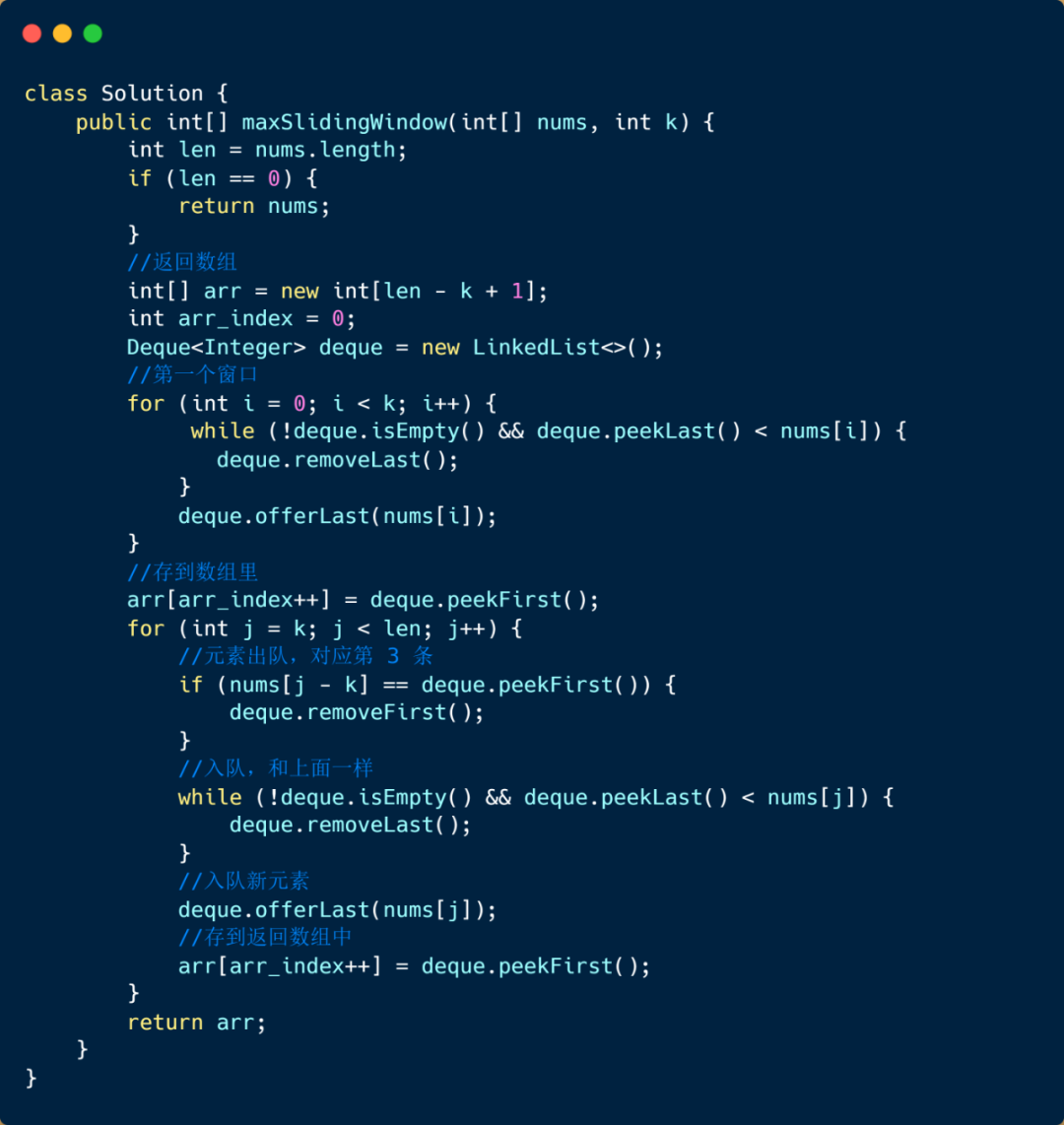
單調棧
leetcode 155 最小棧
設計一個支持 push ,pop ,top 操作,并能在常數時間內檢索到最小元素的棧。
push(x) —— 將元素 x 推入棧中。
pop() —— 刪除棧頂的元素。
top() —— 獲取棧頂元素。
getMin() —— 檢索棧中的最小元素。
輸入:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
輸出:
[null,null,null,null,-3,null,0,-2]
題目解析
感覺這個題目的難度就在讀懂題意上面,讀懂之后就沒有什么難的了,我們在上面的滑動窗口的最大值已經進行了詳細描述,其實這個題目和那個題目思路一致。
該題讓我們設計一個棧,該棧具有的功能有,push,pop,top等操作,并且能夠返回棧的最小值。比如此時棧中的元素為 5,1,2,3。我們執行 getMin() ,則能夠返回 1。這塊是這個題目的精髓所在,見下圖, 這個題目也可以不利用輔助棧解決,但是不符合本文主題,所以在這里先不進行詳細描述。大致思路為,把當前最小值用一個變量保存,需要入棧的值小于當前最小值時,先把當前最小值入棧,再將需要入棧的值入棧,并更新當前最小值。如果大于當前最小值,則直接入棧。getMin()函數則直接返回變量保存的值即可。下面我們來看一下我們借助輔助棧,如何解決這個題目吧。

我們一起先通過一個視頻先看一下具體解題思路,通過視頻一定可以整懂的,我們注意觀察棧 B 內的元素。
我們來對視頻進行解析
1.我們執行入棧操作時,先觀察需要入棧的元素是否小于棧 B 的棧頂元素,如果小于則兩個棧都執行入棧操作。
2.棧 B 的棧頂元素則是棧 A 此時的最小值。則 getMin() 只需返回棧 B 的棧頂元素即可。
3.出棧時,需要進行對比,若棧 A 和棧 B 棧頂元素相同,則同時出棧,出棧后B 的棧頂保存的仍為此時棧 A 的最小元素
題目代碼

leetcode 739 每日溫度
題目描述:
請根據每日 氣溫 列表,重新生成一個列表。對應位置的輸出為:要想觀測到更高的氣溫,至少需要等待的天數。如果氣溫在這之后都不會升高,請在該位置用 0 來代替。
示例1:
輸入:temperatures = [73, 74, 75, 71, 69, 72, 76, 73]
輸出:arr = [1, 1, 4, 2, 1, 1, 0, 0]
示例2:
輸入:temperatures = [30,30,31,45,31,34,56]
輸出:arr = [2,1,1,3,1,1,0]
題目解析
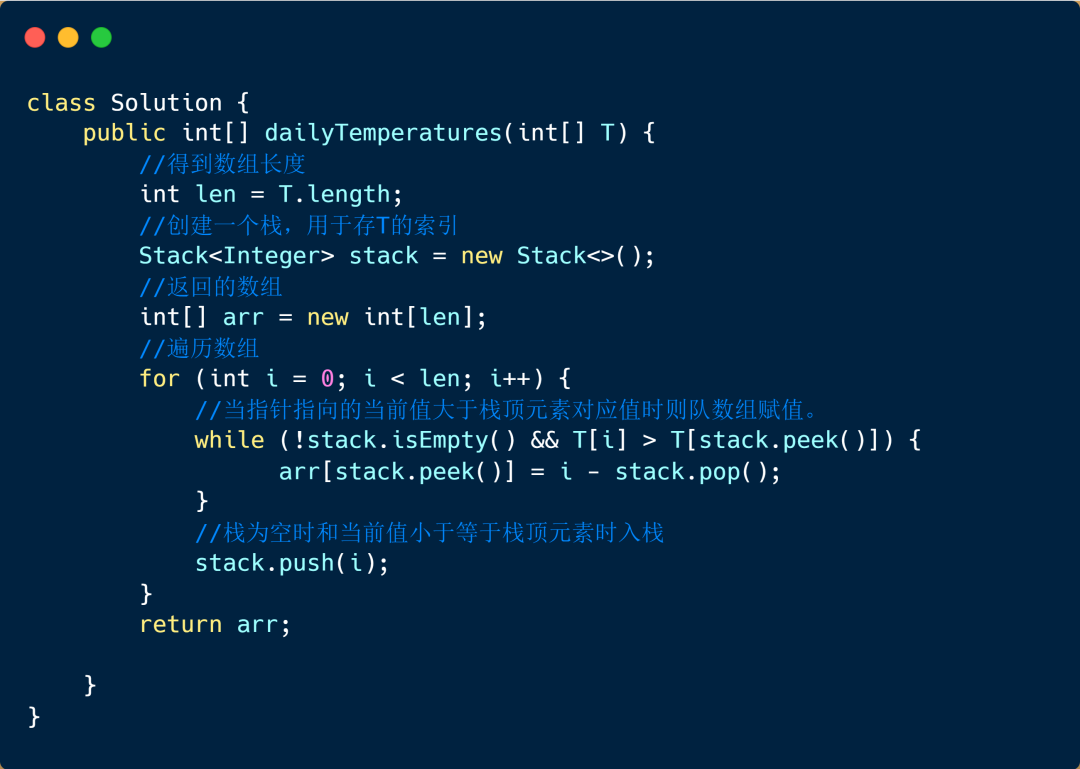
其實我們可以換種方式理解這個題目,比如我們 temperatures[0] = 30,則我們需要找到后面第一個比 30 大的數,也就是 31,31的下標為 2,30 的下標為 0 ,則我們的返回數組 arr[0] = 2。理解了題目之后我們來說一下解題思路。
遍歷數組,數組中的值為待入棧元素,待入棧元素入棧時會先跟棧頂元素進行對比,如果小于等于該值則入棧,如果大于則將棧頂元素出棧,新的元素入棧。
例如棧頂為69,新的元素為72,則69出棧,72入棧。并賦值給 arr,69 的索引為4,72的索引為5,則 arr[4] = 5 - 4 = 1,這個題目用到的是單調棧的思想,下面我們來看一下視頻解析。
注:棧中的括號內的值,代表索引對應的元素,我們的入棧的為索引值,為了便于理解將其對應的值寫在了括號中
leetcode 42 接雨水
這道接雨水也是一道特別經典的題目,一道必刷題目,我們也用單調棧來解決。下面我們來看一下題目吧
題目描述:
給定 n 個非負整數表示每個寬度為 1 的柱子的高度圖,計算按此排列的柱子,下雨之后能接多少雨水。
示例1:
輸入:height =[0,1,0,2,1,0,1,3,2,1,2,1]
輸出:6
示例2:
輸入:height =[4,2,0,3,2,5]
輸出:9
示例2:
輸入:[4,3,2,0,1,1,5
輸出:13
題目解析:
看了上面的示例剛開始刷題的同學可能有些懵逼,那我們結合圖片來理解一下,我們就用示例3的例子進行舉例,他的雨水到底代表的是什么。輸入代表的是黃色箱子的個數,藍色箱子代表雨水數量。縫隙之間可以裝多少水
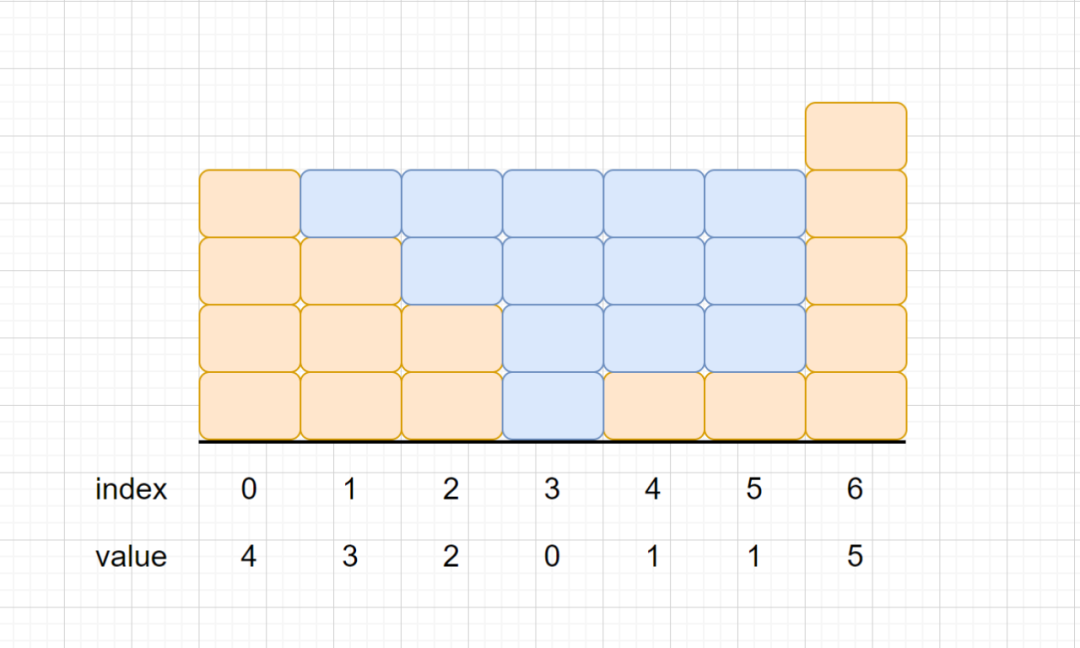
說明:上面是由數組 [4,3,2,0,1,1,5]表示的高度圖,在這種情況下,可以接 13個單位的雨水(見下圖)。
上圖則為我們的題目描述,是不是理解了呢?你也可以這樣理解我們在地上放置了若干高度的黃色箱子,他們中間有空隙,然后我們想在他們里面插入若干藍色箱子,并保證插入之后,這些箱子的左視圖和右視圖都不能看到藍色箱子。 好啦題目我們已經理解了,下面我們來看一下接雨水問題到底該怎么做,其實原理也很簡單,我們通過我們的例3來進行說明。 首先我們依次入棧4,3,2,0我們的數組前四個元素是符合單調棧規則的。但是我們的第五個1,是大于0的。那我們就需要0出棧1入棧。但是我們這樣做是為了什么呢?有什么意義呢?別急我們來看下圖。
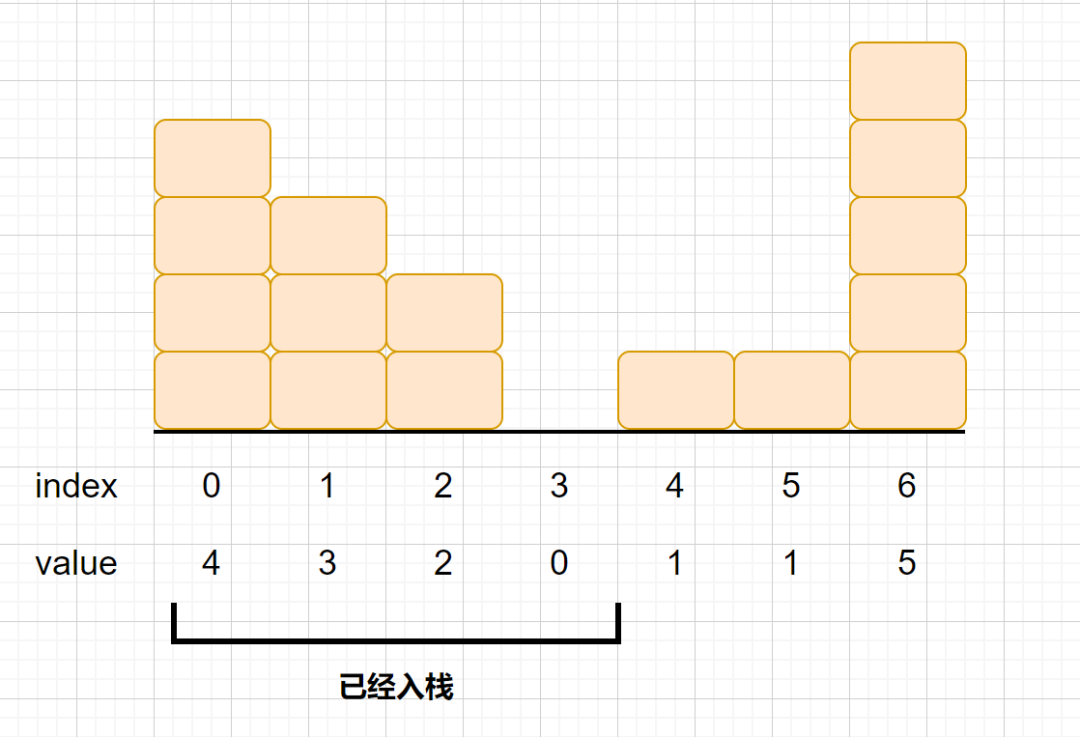
上圖我們的,4,3,2,0已經入棧了,我們的另一個元素為1,棧頂元素為0,棧頂下的元素為2。那么我們在這一層接到的雨水數量怎么算呢?2,0,1這三個元素可以接住的水為一個單位(見下圖)這是我們第一層接到水的數量。 注:能接到水的情況,肯定是中間低兩邊高的情況
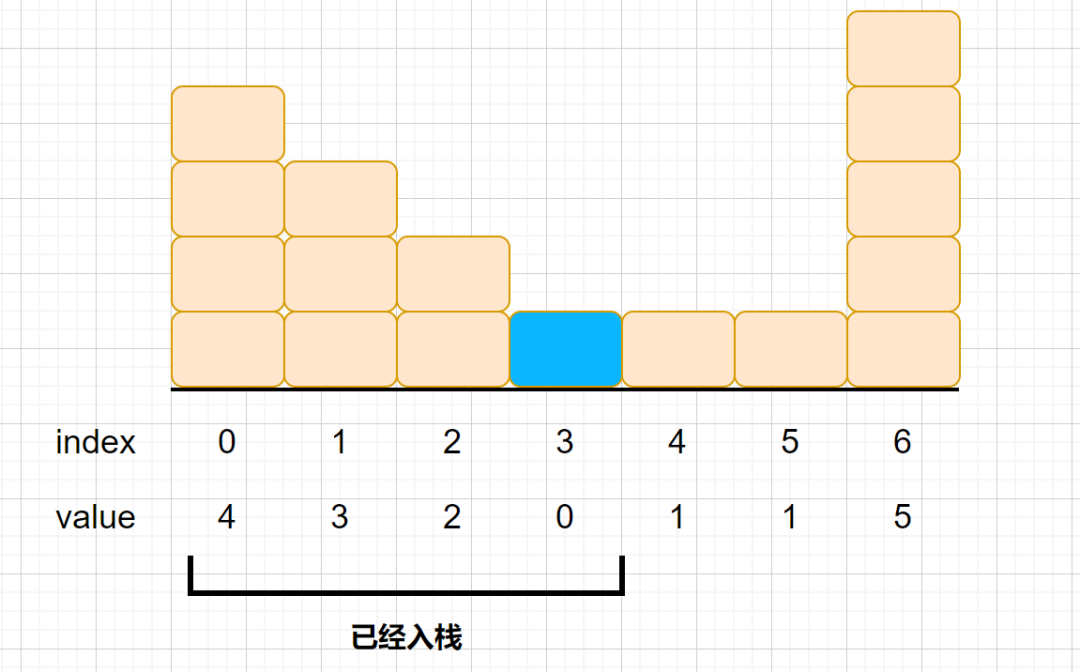
因為我們需要維護一個單調棧,所以我們則需要將0出棧1入棧,那么此時棧內元素為4,3,2,1。下一位元素為1,我們入棧,此時棧內元素為4,3,2,1,1。 下一元素為5,棧頂元素為1,棧頂的下一元素仍為1,則需要再下一個元素,為2,那我們求當前層接到的水的數量。 注:棧內保存的應是索引值,這里為了便于理解用了value值

我們是通過2,1,1,5這四個元素求得第二層的接水數為1*3=3;1是因為min(2-1,5-1)=min(1,4)得來的,大家可以思考一下木桶效應。裝水的多少,肯定是按最短的那個木板來的,所以高度為1,3的話是因為5的索引為6,2的索引為2,他們之間共有三個元素(3,4,5)也就是3個單位。所以為6-2-1=3。 將1出棧之后,我們棧頂元素就變成了2,下一元素變成了3,那么3,2,5這三個元素同樣也可以接到水。
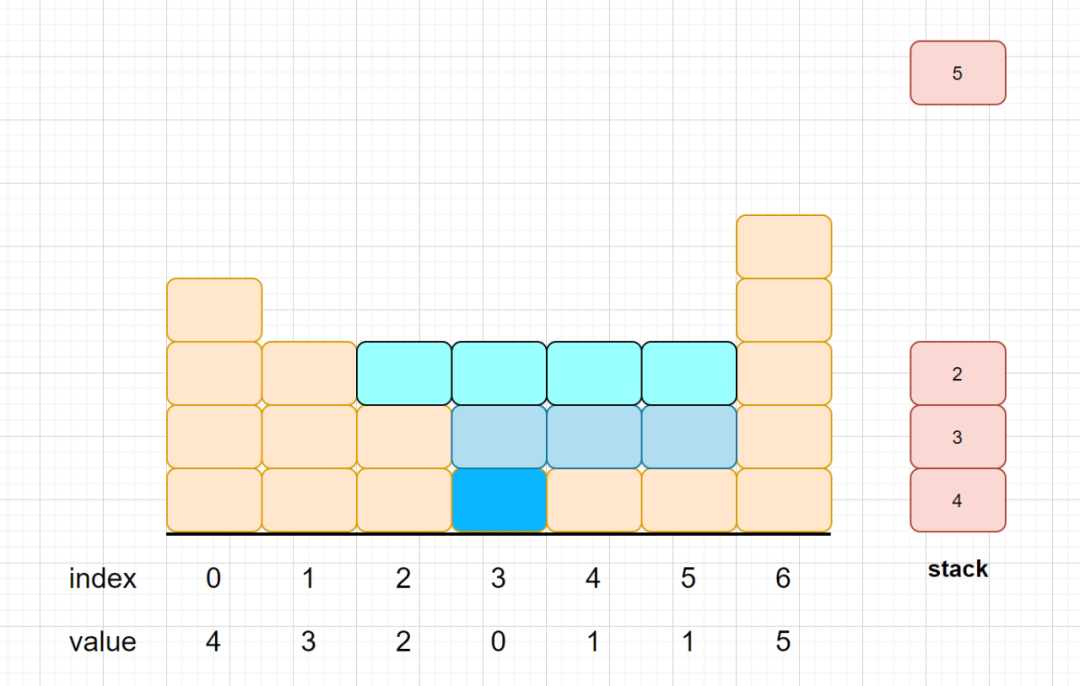
這是第三層的接水情況,能夠接到4個單位的水,下面我們繼續出棧2,那么我們的4,3,5仍然可以接到水啊。
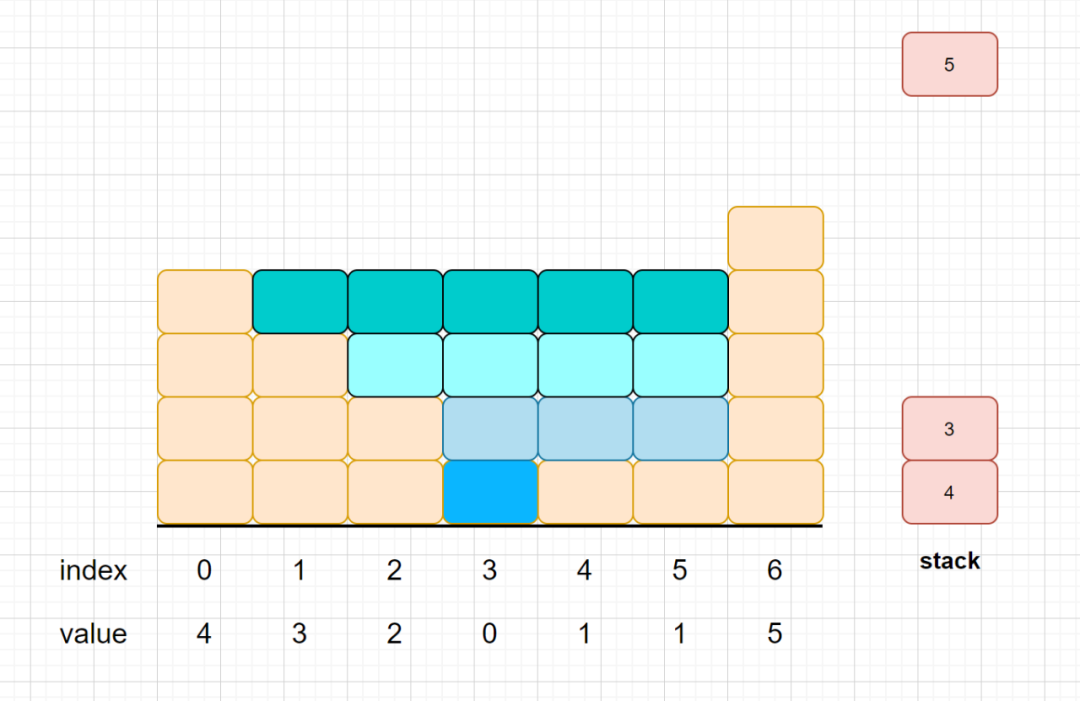
這是我們第四層接水的情況,一共能夠接到5個單位的水,那么我們總的接水數加起來,那就是1+3+4+5=13。你學會了嗎?別急還有動圖我們,我們再來深入理解一哈。
題目代碼:
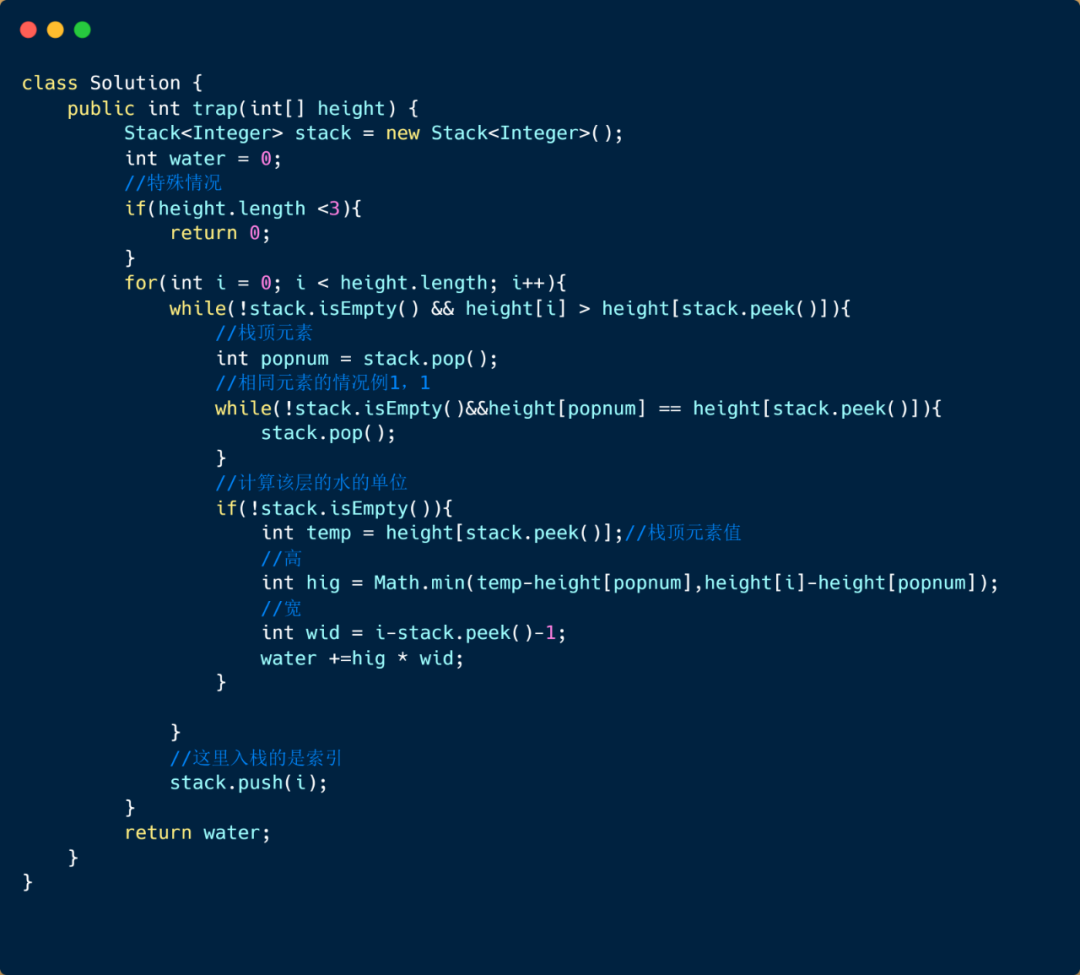
好啦,咱們的單調隊列和單調棧的題目到這里就算總結完畢啦,希望對你能有一點點幫助。
原文標題:深入淺出搞通單調隊列單調棧
文章出處:【微信公眾號:嵌入式ARM】歡迎添加關注!文章轉載請注明出處。
責任編輯:haq
原文標題:深入淺出搞通單調隊列單調棧
文章出處:【微信號:gh_c472c2199c88,微信公眾號:嵌入式微處理器】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
RabbitMQ消息隊列解決方案
程序設計與數據結構
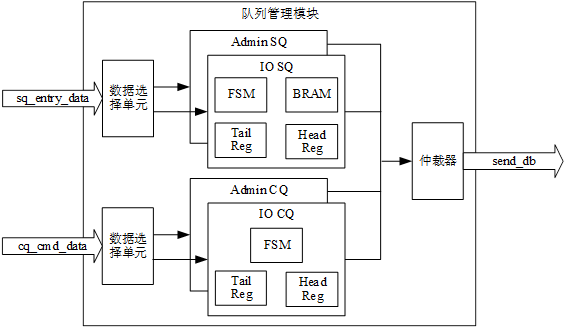
NVME控制器之隊列管理模塊
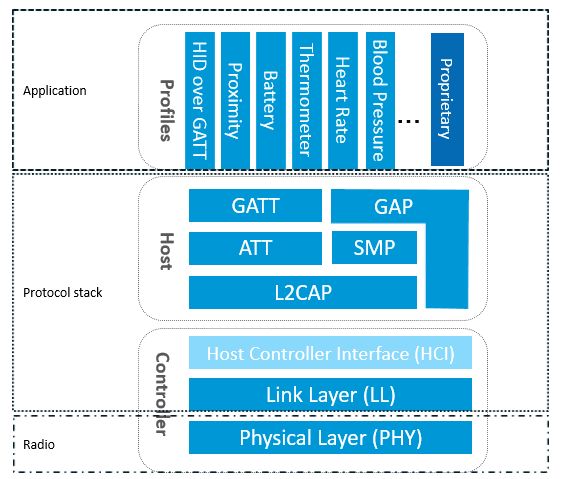
深入淺出解析低功耗藍牙協議棧



















評論