當前，電子設備的主要失效形式之一就是熱失效。據統計，電子設備的失效有55％是溫度超過規定值引起的，隨著溫度的增加，其失效率呈指數增長。對于很多電子設備，即使是溫度降低1℃，也將使設備的失效率降低一個可觀的量值。因此，電子設備的熱設計越來越受到重視，采用合理的熱設計，提高散熱系統的性能成為保證電子產品整體可靠性的關鍵技術之一。

針對封裝散熱結構優化問題中存在的難點，本文提出了一種基于近似模型和隨機模擬的快速全局優化方法。建立封裝散熱結構的高精度近似模型，能夠有效地控制優化設計中仿真分析的重復次數，協調計算成本和計算精度這一對矛盾。隨機模擬能夠很好地解決混合離散變量優化問題，并且魯棒性好、全局尋優能力強。最后以方形扁平封裝器件（QFP）為例，應用該方法實現了封裝散熱結構的優化。

1 近似模型

1.1 近似模型的產生

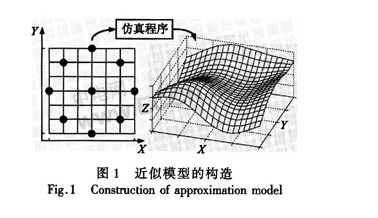
所謂近似模型是指計算量小，但計算結果與仿真程序相近的分析模型。在優化過程中，用近似模型替代仿真程序能夠克服計算量過大的問題。構造近似模型需要三個步驟：①根據試驗設計生成若干樣本點；②用仿真程序（如CFD、FEA等）對樣本點進行分析，獲得輸入／輸出數據；③在輸入／輸出數據的基礎上構造出近似模型，如圖1所示。為了控制仿真分析的重復次數，本文將建立封裝散熱結構的高精度近似模型，具體思路是將Kriging建模技術與CVT試驗設計相結合。

1.2 Kriging近似模型

式中，F是由樣本點處f（x）的值構成的矩陣；R為相關矩陣，即R（i，j）=R（si，sj）。在求解式（3）之前，需要先求出相關函數中的相關參數θ，對它的求解可以轉化為如下的優化問題

式中，r（x）為相關向量。與其他模型相比，Kriging模型有以下優勢：沒有對未知函數的形式作任何限制性假定；能自適應地調整各個樣本點上分配的權值；考慮了回歸誤差項的空間相關性。對Kriging方法更詳盡的論述可參閱文獻［2-3］。

1.3 CVT試驗設計

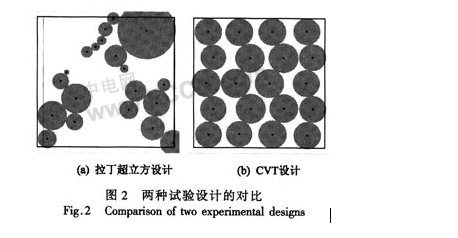
試驗設計是安排仿真試驗的方法，它決定了構造近似模型所需的樣本點。最近發現，CVT設計的某些性能（樣本點分布均勻度、所構造模型的精度）優于流行的拉丁超立方設計。圖2對二者進行了比較，為便于觀察，以每個樣本點為圓心作圓，并且設法保證該圓與以最鄰近樣本點為圓心的圓外切。圖2（b）中各圓半徑相差不大，并能覆蓋住絕大部分區域，具有很均勻的空間分布特性；而圖2（a）中樣本點的空間分布特性是很不穩定的。本文采用CVT設計來構造近似模型。

1.4數值算例

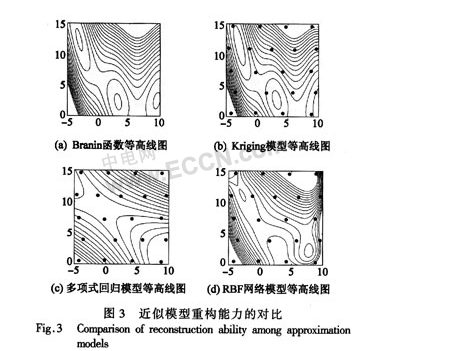
根據Jones的建議，以等高線圖來評價近似模型的性能。圖3（a）為Branin函數，圖3（b）為Kriging模型，同時示出CWT樣本點。在圖3（a）與圖3（b）中，等高線的形狀和最優點的位置都很接近。圖3（c）中的多項式回歸模型有嚴重的形狀失真，而且幾乎完全遺漏了最優點的位置。圖3（d）為RBF神經網絡，它稍優于多項式回歸模型，但還是不如Kriging模型。因此，在三種模型中Kriging的重構能力最強。

2基于隨機模擬的優化方法

隨機模擬是目前幾種主要的約束非線性離散優化方法之一。它通用性強，對目標函數、約束條件以及離散變量的個數沒有特殊要求，并且容易獲得全局最優解。但其缺點也很突出，需要成千上萬次地求解目標函數，容易造成計算開銷過大，該問題可以通過使用近似模型加以解決。近似模型與隨機模擬相結合不僅解決了計算量大的問題，而且使它們各自的優勢得到了最大程度的發揮，本文采用這一方法來對封裝散熱結構進行優化。

隨機模擬還需要避免重復抽樣。重復的試驗樣本占用了計算時間卻不提供有效信息，嚴重地影響著尋優效率。為解決這一問題，本文在隨機模擬中采用了Quasi-Monte Cado法。與經典Monte Carlo法不同，Quasi-Monte Carlo法的抽樣過程具有“記憶”特性，它的試驗樣本是按照擬隨機序列選取的，其生成算法保證了試驗樣本之間總是“盡可能地相互回避”。在抽樣的任何階段，相繼的試驗樣本都“知道”前面的空隙在哪里，從而避免了重復抽樣，提高了尋優的效率。

3 應用實例

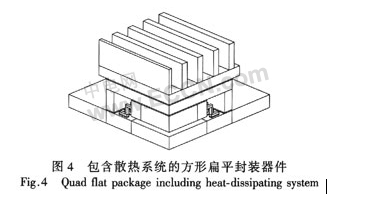
本文以包含散熱系統的方形扁平封裝器件為研究對象（圖4）。該模型作了如下假設和簡化：根據對稱性取1／4結構進行分析；對引線和焊點的形態進行了簡化；外部的對流換熱只以自然對流的方式進行。

在文獻［6］的基礎上，本文采用參數化設計語言APDL組織和管理有限元分析命令，使溫度場仿真過程實現了完全的參數化，根據幾何實體間的相對位置關系來選定需要進行操作的實體。結構的有限元模型如圖5所示。

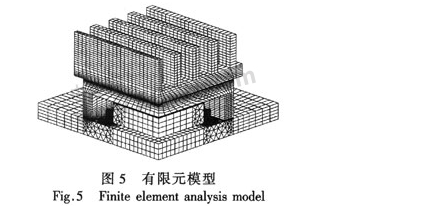
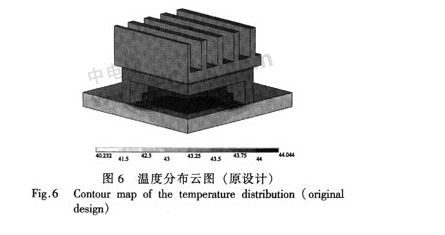
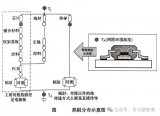
芯片發出的熱量在結構中以熱傳導的形式進行傳遞，到達外表面后以對流和輻射的形式進行散熱。通過溫度場仿真，發現作為熱源的芯片溫度最高，沿著熱量傳輸的路徑溫度呈下降分布，最高溫度出現在芯片的中心，為44.044℃，如圖6所示。為了提高芯片的可靠性，充分挖掘散熱系統的潛力，本文試圖通過改進封裝散熱結構的設計來降低芯片溫度。

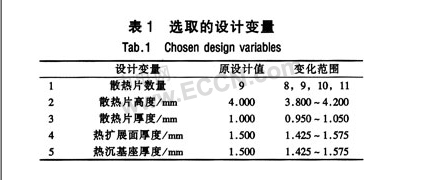
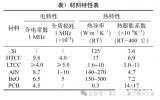
考慮如下設計變量：散熱片數量、散熱片高度、散熱片厚度、熱擴展面厚度和熱沉基座厚度，其原設計值和參數變化范圍如表1所示。以芯片中心溫度為優化目標，并施加約束條件，封裝總高度不得超過原高度的101％。

根據Jones的“10倍準則”，調用Researchsampling software工具箱，采用CVT試驗設計選取59個樣本點，并按照指定格式將其編寫成自定義重分析文件。然后ANSYS就可以根據該文件和前面建好的參數化分析流程自動進行重分析，獲得相應的輸入／輸出數據。在這組數據的基礎上，調用DACE工具箱，根據Kriging方法構造出封裝散熱結構溫度場仿真的近似模型。

接下來利用隨機模擬進行尋優計算。根據Quasi-Monte Carlo法，首先借助Research samplingsoftware工具箱生成5維的擬隨機序列，再將其映射到設計空間。然后根據所施加的約束條件，從中挑選出可行解，構成可行試驗樣本序列。最后，在可行試驗樣本序列和前面建好的近似模型的基礎上進行隨機模擬。經過103 884次模擬，得到了優化結果：散熱片數量為11，散熱片高度為4.20 mm，散熱片厚度為1.04 mm，熱擴展面厚度為1.44 mm，熱沉基座厚度為1.49 mm，此時芯片中心溫度的Kriging預測結果為42.319℃。

將上述設計參數代入ANSYS的APDL分析文件，經過溫度場仿真，發現芯片中心溫度的有限元計算結果為42.324℃（圖7），與預測結果十分接近，僅相差0.005℃，這說明所建立的近似模型具有很高的精度。盡管如此，對該模型進行求解所需的時間卻很短，超過10萬次的求解只需十幾秒鐘，而在同一PC上進行一次有限元溫度場仿真卻需要將近4 min。因此使用近似模型代替仿真程序能夠大大提高隨機模擬優化的計算效率。

優化后封裝總高度比原來增加了0.96％，已經基本達到了可行域的邊界。優化后的芯片中心溫度為42.324℃，相對于原先的44.044℃有了明顯的降低。如果需要進一步降低芯片工作溫度，可以考慮使用強迫對流換熱。

為了進一步驗證Kriging近似模型的有效性，從可行試驗樣本序列中隨機選取70個樣本作為測試樣本，然后分別用有限元程序和Kriging模型對測試樣本進行分析，并計算出Kriging預測結果與有限元分析結果之間的差值，該差值就是Kriging近似模型的預測誤差。Kriging模型在這70個測試樣本上所產生的預測誤差Ep如圖8所示。

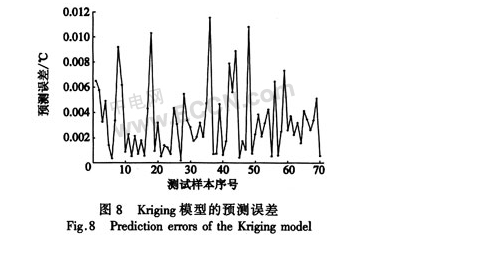
可以看出，Kriging模型在測試樣本集合上所產生的最大預測誤差也只為0.01～0.012℃，完全能夠滿足優化設計的需要。

4結論

針對封裝散熱結構優化問題中存在的難點，提出了一種基于近似模型和隨機模擬的快速全局優化方法。建立封裝散熱結構的近似模型，能夠有效地控制優化設計中仿真分析的重復次數。所采用的Kriging模型具有很高的預測精度，數值算例的分析結果表明，它對未知目標函數的重構能力明顯高于多項式回歸模型和RBF神經網絡；同時，具有良好空間均勻性的CVT試驗設計使Kriging模型的泛化能力達到了最大程度的發揮。

基于隨機模擬的優化解決了設計變量中含有離散變量的問題，在隨機模擬中采用了Quasi-Monte Carlo法，有效地提高了尋優的效率。最后以方形扁平封裝器件為例，以芯片的中心溫度為優化目標，應用該方法實現了封裝散熱結構的優化，獲得了令人滿意的結果。近似模型方法很好地協調了優化設計中計算成本和計算精度這一對矛盾，顯著地提高了隨機模擬優化的計算效率，具有推廣應用價值。

編輯：jq