一、關于IIR數字濾波器

當然關于IIR濾波器的知識，想必大家在教材上都已經很熟了，這里我就簡單說一下自己的理解好了。

正如前面說的，IIR數字濾波器，即無限長單位脈沖響應數字濾波器。所謂無限長單位脈沖響應，也就是說，對于一個系統，我們給其輸其激勵，在輸出端得到的一串序列hn是無限長的，又因為我們討論的都是因果系統，即只考慮n大于零的部分，所以，hn可以表示為0《= hn 《 無窮大。

前面還說了，IIR區別于FIR濾波器的還一個特點就是他的反饋結構，即IIR濾波器的輸出，不僅與輸入激勵有關，還與當前的輸出值也有關，用差分方程來表示就是

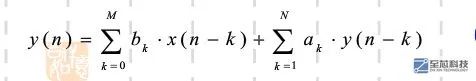
根據這個差分方程可以看出：

1、跟FIR濾波器的差分方程進行對比的話會發現，IIR濾波器的差分方程等式右邊的前半部分跟FIR濾波器的差分方程類似，都是對輸入信號進行的卷積運算，只不過FIR濾波器是將輸入信號與系統的單位脈沖響應進行卷積，而這里是輸入信號跟IIR濾波器的零點系數進行卷積

2、后半部分是IIR濾波器的極點部分，也可以看做是一個N階的FIR濾波器，運算對象是系統的輸出信號的一部分與極點系數的一部分。

3、因此，IIR濾波器的輸出就可以看成是 兩個FIR濾波器的運算，即

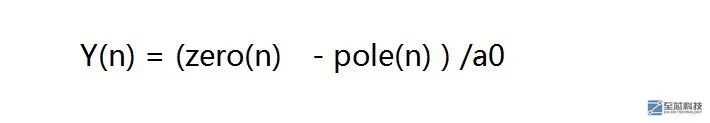
ao即Y（n）的系數

然而IIR濾波器的表示形式還有一種方式，就是我們常說的系統函數，即對差分方程中的輸入輸出進行Z變換，并通過移位運算得到H（z），而它也就是系統單位脈沖響應的Z變換

二、關于零極圖

我們知道，系統函數的分子分母都是一個乘加多項式，既然這樣，分子分母就可以進行因式分解，也就是我們書本上的系統的零極點表達式

零極圖的作用可不小，既然我們濾波器的系統函數完全可以用零極點來表示，也就是說，我們濾波器的性質，也可以通過零極圖來分析，比如可以通過零極圖來看系統的單位脈沖響應的形狀，系統的因果性與穩定性之類的

1、零極圖與單位脈沖響應

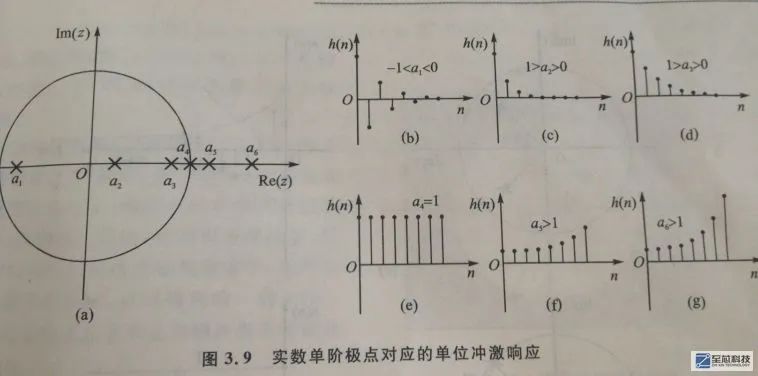
看上面這張圖，現在假如有個IIR數字濾波器，假設只有一個極點，極點位置的不同會導致濾波器單位脈沖響應形狀的不同，總結如下：

1、極點在單位圓內時，單位脈沖響應的形狀呈下降收斂狀，極點在單位圓上時，單位脈沖響應的形狀呈直線狀，極點在單位圓外時，單位脈沖響應的形狀呈上升發散狀，且離單位圓越遠，放大倍數越大

2、單位脈沖響應的形狀主要是由濾波器的極點位置決定，零點位置主要是影響單位脈沖響應的幅度特性和相位特性（上圖中雖然沒有畫出零點，大家可以通過matlab仿真總結出這條結論）

2、零極圖與濾波器的因果性，穩定性

通過教材我們已經知道了，我們所研究的都是因果系統，而因果系統的收斂域不包括任何一個極點。為什么呢？因為極點是導致系統函數趨于無窮大的點，一旦收斂域包含了極點，那就會導致系統函數不收斂，因此，因果系統的收斂域必須大于離單位圓原點最遠的那個極點，也就是說，只要知道了一個因果系統的極點分布，那么他的收斂域也就已經確定了。假如定義一個系統的極點分別為 ： 1 ，-2，0.5，-3，那么這個系統的收斂域就是 z 》 3.

關于穩定性問題，我們知道，只有當系統函數的收斂域包含單位圓的時候，單位脈沖響應絕對可和，這時候系統才是穩定的，又由于之前說的因果性， 系統函數的收斂域不能包含任何一個極點，因此我們知道，只有當極點在單位圓內的時候才符合要求，因此，極點在單位圓內成了系統穩定的必要條件。

三、關于IIR濾波器的設計方法

其實，我們書本上介紹的什么脈沖響應不變法，雙線性變換法之類的設計方法，設計過程都太過于繁瑣，想必大家都深有體會，可能原理不是很難理解，但是真正讓我們去手動去算一個題，還不知道要算到什么時候。但是matlab為我們提供好了設計函數，我們甚至不需要知道那些變換方法，也可以設計出符合要求的濾波器。但是，書本上既然寫了，總有他寫這些東西的目的，可能我們實在不好理解他的運算過程，但是也要大體上知道這回事，畢竟人家是當時的科學巨匠的畢生心血，哪有那么好懂~是吧，我們只要是會用就不錯了，下面就簡單總結一下這幾種方法：

IIR數字濾波器都是經過低通模擬濾波器變換而來的，因為模擬濾波器的理論已經很成熟了，而且有大量的數據供我們直接使用，比如巴特沃斯濾波器的設計過程，已經給我提供好了求最小濾波器階數和零極點的公式，只要我們將濾波器指標帶進去計算就好了。

至于這些公式怎么來的，說實話我也看不懂，只知道是一大片數學公式推導而來，很多朋友一看到這群數學公式肯定就迷糊了，甚至是失去了學習的興趣了，太過繁瑣的數學公式的推導，使得我們的教材變得枯燥無味，我是過來人我深有體會，雖然這樣的教材很嚴謹，但是卻抹殺了學生的積極性，并沒有取得好的教學目的，其實還是感覺那句老話說的對“高手在民間啊”，很多一些不出名的關于信號處理的書，卻硬是把信號處理這門課寫的生動有趣，讓人一讀便懂，甚至有種豁然開朗的感覺。再反觀我們使用的教材，雖然獲得了什么什么教學獎，然而感覺并沒有真正站在學生的角度在寫這本書，學生看到只是大片的數學公式，也就喪失了信心了。

常用的模擬濾波器設計模型大概有這幾種，巴特沃斯濾波器，切比雪夫濾波器、和橢圓濾波器，這幾個濾波器都模擬低通濾波器，要想得到其他類型的濾波器，需要經過變換，然而這幾種提供了詳細的設計資料，有了這些資料，我們就能通過變換將其變換為我們需要的其他類型的數字濾波器。

例如，我想設計一個IIR帶通濾波器，根據需要

1、 我需要先確定濾波器指標，主要包括通帶最大衰減，阻帶最小衰減，通帶截止頻率，阻帶截止頻率

2、有了這4個模擬帶通濾波器的指標，我們可以用頻率變換公式將這4個指標轉換為相應模擬低通濾波器的指標。

3、有了低通濾波器的指標，就可以根據經典濾波器的資料，設計成相應的模擬低通濾波器。

4、 對模擬低通濾波器進行頻率變換，得到我們想要的模擬帶通濾波器

5、最后可以通過脈沖響應不變法或者雙線性變換法，得到我們需要的數字帶通濾波器

下面就總結一下這兩種變換方法

脈沖響應不變法

上面說了，需要通過脈沖響應不變法或者雙線性變換法將模擬帶通濾波器轉換為我們需要的數字帶通濾波器。既然是模擬濾波器，也就是說，是單位脈沖響應ht的拉普拉斯變換，如果對模擬濾波器的系統函數進行逆拉普拉斯變換就可以得到ht，有了ht，再通過抽樣不就可以轉化為hn了嘛，所以，脈沖響應不變法可以總結如下：

1、對模擬濾波器的系統函數進行逆拉普拉斯變換得到時域上連續的系統的單位沖激響應ht

2、對ht進行n點等間隔抽樣，得到時域上離散的系統的單位脈沖響應hn

3、對hn進行Z變換，得到數字濾波器的系統函數H（Z）

需要注意的是，在對時域上連續信號進行等間隔抽樣的時候，我們知道，時域抽樣等同于頻域的周期延拓，如果不滿足一定的條件，就會導致信號的頻域混疊 ，而這個條件，就是我們采樣定理所給出的，即必須得保證模擬濾波器的帶寬是有限帶寬，并且采樣頻率fs 》 2fmax.

看下面這張圖我來解釋一下

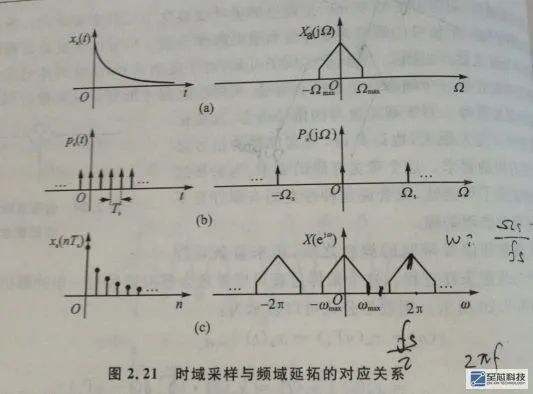
這里我來解釋一下采樣定理，假如有一個帶限模擬信號，他的時域和頻域波形如圖第一排所示，可以看到在頻域，他的帶寬為2Ωmax，即最大角頻率為Ωmax

而Ωmax= 2πfmax，這里的fmax是模擬頻率，單位是hz，跟角頻率不同

現在用一個頻率為fs的信號對原模擬信號在時域進行等間隔抽樣，采樣信號在頻域的波形如圖第二排所示，角頻率Ωs = 2πfs，是一個周期為Ωs的周期信號

圖上第三排是模擬信號經采樣后的時域波形與頻域波形，時域波形很直觀，就是由連續信號變為了離散信號，頻域波形變成了原模擬信號波形的周期延拓，周期為2π

大家知道，在數字頻域，角頻率w = Ω / fs ，所以我們看到在Ωs的正下方對應的是2π，數字頻域0到2π之間對應的當然就是π，而這里的π對應的模擬頻率，當然就是fs/2，而數字頻域的wmax 則對應 Ωmax / fs ，即 wmax = 2πfmax / fs

所以，要想保證經采樣后的信號的頻譜不發生頻率混疊，就必須要保證wmax 《 π

因此推得 fs 》 2fmax

正是因為如此，脈沖響應不變法只能用來設計低通和帶通濾波器，不能設計高通和帶阻濾波器，因為后兩者在數字頻域π處均存在頻譜分量

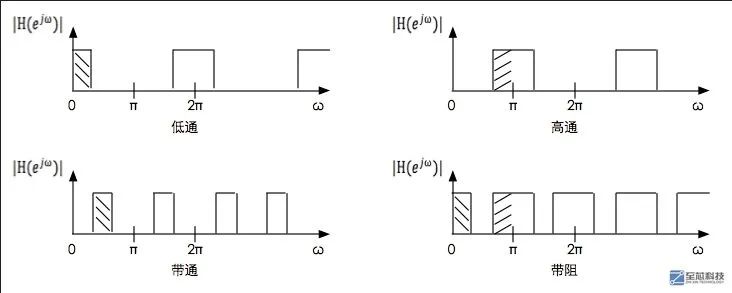
雙線性變換法

雙線性變化法相對于脈沖響應不變法適應性更強，不存在混疊失真的情況，但是計算過程也是相當的復雜，具體過程其實書上都有寫，只不過就是太過繁瑣，讓人看得不爽。好在matlab為我們提供了設計好的函數，matlab工具箱里的函數 butter ellip cheby1 cheby2 等函數都是基于雙線性變換法來設計的函數，可以直接將跳過復雜的設計過程，由我們制定的濾波器指標直接生成數字濾波器的零極點系數。

既然這樣，我們之前還那么多廢話干什么？直接講matlab設計不就好了？其實并不是這樣，知識是一個體系，只有有了前面的知識做鋪墊，才能為以后的設計打下基礎，要不然只會調用matlab函數，不懂為什么這樣的，到后面就遇到瓶頸了。

好了，在了解這些理論知識之后我們就可以來設計我們的濾波器，其實當這些東西都掌握的差不多的時候，你會發現設計濾波器并不是很難

和FIR濾波器一樣，我先把濾波器要求說明一下，然后再按照設計要求進行設計

四、IIR濾波器的matlab設計與FPGA實現

要求設計一個IIR低通數字濾波器，要求：：

1、 設計成切比雪夫II型濾波器

2、截止頻率為500hz，阻帶最小衰減為60db，采樣頻率為2000hz，，濾波器階數為7

3、合成信號為100，500，800hz的正弦信號的疊加

4、要求分別采用直接II型結構和級聯型結構分別在FPGA上實現，并通過modelsim仿真出濾波后的100HZ正弦波

5、級聯結構為了提高運行速度采用流水線結構設計

6、通過matlab對modelsim輸出的數據進行仿真，看是否符合要求

前面說過了，matlab為我們提供了IIR濾波器設計的工具箱，我們可以直接調用函數，就可以直接由濾波器指標設計成數字濾波器

如上圖所示，我們直接調用cheby2型函數，送人濾波器設計指標，直接就可以設計出符合要求的濾波器，可以說，就這么幾行代碼，一個濾波器就設計完成了。但是，我們不僅要設計出濾波器，還要實現它，并且是FPGA硬件實現，光有這些數據是不行的，上面設計的濾波器輸出如下

可以看到，這些數據是無法在FPGA上實現的，我們需要將他們量化，具體進行多少bit的量化才可以設計出符合要求的濾波器，需要通過matlab仿真才知道。當然，由上面的系數構成的濾波器是理想濾波器，當然他們的位數不僅僅是這幾位，是因為matlab顯示的原因，后面還有很多位數沒有顯示出來，要知道，我們是要將這些數據送到FPGA內部的寄存器中進行運算的，不可能將所有位數都表示完整，只能表示個近似值，這就導致了有限字長效應，使得實際濾波器與理想濾波器還是有些差別的，因此，我們需要將這些系數進行量化，將量化后的濾波器系數求出幅頻響應，與理想濾波器的幅頻響應進行對比，來確定量化位數

上圖就是通過仿真來確定濾波器的量化位數，函數QuantIIRDirectArith是用來計算實際情況下濾波器的單位脈沖響應的，是人為編寫的函數，其中的算法我們可以不去深究，只知道輸入量化后的濾波器系數和需要濾波器輸出的位數，就可以計算出實際濾波器的輸出情況，與理想濾波器進行對比，從而確定量化位數，這里仿真出來，當量化位數為16的時候，波形就幾乎與理想情況吻合

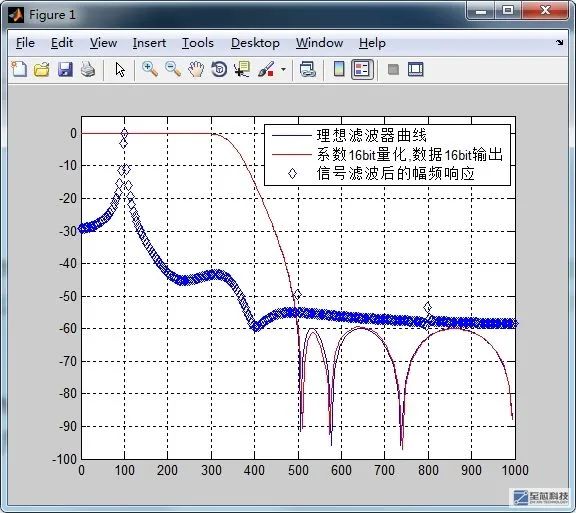
對于系數的量化問題，這里也不能像FIR濾波器一樣直接進行量化了，因為IIR濾波器不僅存在乘加運算，還存在除法運算。前面說了，IIR濾波器的輸出，可以看做是兩個FIR濾波器相減之后再除以系數a（0），這里的系數a（0） 就是極點系數的第一項，既然要除以這個系數，只要保證這個系數是2的整數次冪，就可以通過向右移位的方式來進行相除。例如，經過處理和量化之后，極點系數的第一項為1024，那么就相當于把兩個FIR濾波器的運算結果右移10位就好了

這也可以算是一種算法了，大家可以帶一個數進去試試，就知道這種算法的原理了，經過這種方式的量化后，我們得到的濾波器系數就變為

從這量化后的系數我們可以看出，零點部分完全就是一個FIR濾波器，極點部分還不太像，因為系數不對稱，這樣的話，我們有了濾波器的零極點系數，剩下的就是FPGA實現了。

對于FPGA的實現過程，零點部分完全和FIR濾波器的運算過程相同，就是將輸入信號存入寄存器之后，對輸入信號進行對稱系數累加，再分別與濾波器的零點系數進行相乘，最后將結果相加輸出濾波器極點部分zero（n）

極點部分跟零點部分類似，只有一點稍微需要注意，由于IIR濾波器存在反饋結構，濾波器的輸出也是極點部分的輸入。極點部分的累加相乘跟零點部分稍有不同，首先，極點部分不存在對稱結構，因此不需要將輸入信號進行對稱相加，只需要直接與極點系數相乘。還有就是，極點系數的第一項不參與相乘，因為他是輸出Y（n） 的系數，從第二項開始才進行乘加運算，例如pole_coe（1）*y（n-1） ， pole_coe（2）*y（n-2）。..。..。.

前面說過，零點部分與極點部分進行減法運算，結果再除以Y（n）的系數之后，就是IIR濾波器的輸出

在用FPGA實現IIR濾波器的時候要注意這幾點，我總結如下

1 、 首先要注意，不管是存儲數據的寄存器型變量還是線型變量都不要忘記定義成有符號型數據

2、 要注意字長問題，兩個N位數據相加，至少需要N+1位寄存器存儲結果才能保證結果不溢出，兩個N位數據相乘，至少需要2N位寄存去存儲，大部分情況下，2N-1位就可以了

3、最后的截尾處理，如果不能夠保證截取的位數能夠將輸出的數據完整表示，可以考慮放棄精度，舍棄低位取高位。例如上面，假如我截取sum_div的0到15位不能夠表示IIR濾波器的輸出，也就是說有些IIR濾波器輸出的數據要大于2^15，因此，截尾的時候可以考慮截取1到16位作為結果，這樣做話相當于降低了量化位數，精度降低了，但可以保證輸出正確幅度的波形

下面是將疊加信號進行濾波后的輸出情況

五、級聯結構的IIR濾波器的FPGA實現

其實在實際應用中，應用最廣泛的還是級聯型結構，因為這種結構的系統函數除了一個系數之外完全是由零極點構成，而且占用資源少，速度快。

級聯結構說白了就是幾個直接型結構的IIR濾波器相乘罷了，有了直接型結構的基礎，再來設計級聯結構就很簡單了。

設計級聯結構的關鍵一步就是如何將直接結構的濾波器系數轉換為級聯結構的系數，其實這也是一個算法問題，說實話這個算法我也沒看明白，就是通過一系列的數學運算，將直接型結構轉化為了級聯結構的系數

可以看到，我們設計好直接型結構濾波器之后，直接調用轉換函數，就可以得到級聯結構的濾波器系數，其中b0為增益系數，就是放在零點部分外面的那個系數。轉換函數是人為寫的，我也不太懂為什么是這樣轉換的，既然別人已經做好了這種算法，我們實在看不懂的話就直接拿來用好了

函數Qcoe是量化函數，就是前面講過的，要將極點系數量化為2的整數次冪的量化函數。

經過這樣的處理之后，就會得到了四個直接型結構的IIR濾波器，每階IIR濾波器的計算方法都跟前面直接型濾波器的計算方法相同，這里不做解釋。

級聯型結構在進行FPGA實現的時候要注意每一階濾波器的輸出數據的位寬，即通過matlab仿真出每級濾波器輸出數據的最大值，算一下用多少位的寄存器才能表示這個數值，下面是合成信號依次通過各級濾波器，并計算每通過一級濾波器后的輸出位寬

合成信號每通過一級濾波器，就相當于對信號進行了一次濾波，通過仿真可以看到，每通過一級濾波器，輸出的信號更加趨于圓滑

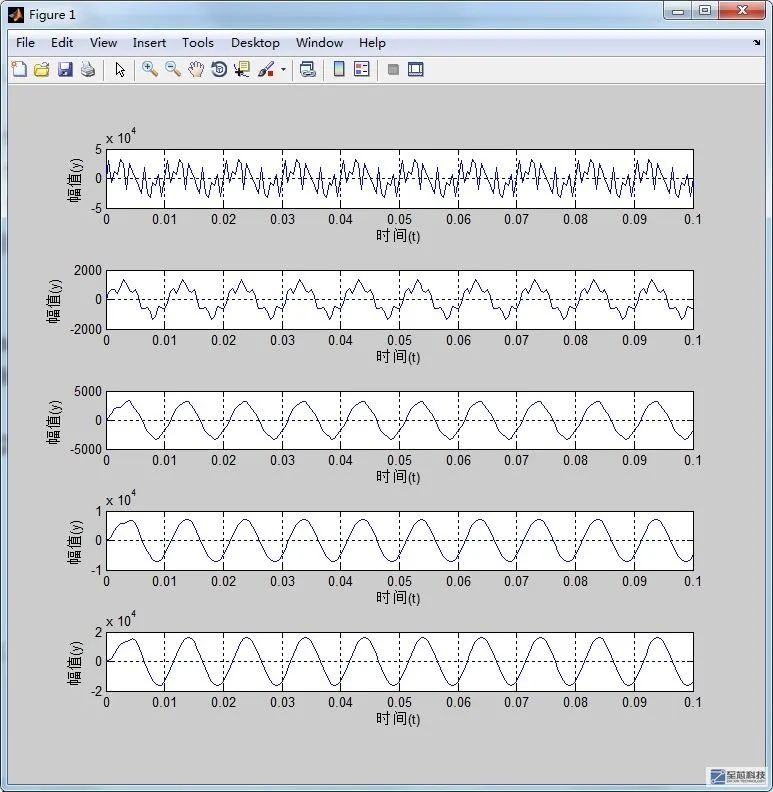
級聯結構的FPGA實現過程是比較費勁的，因為要設計多級濾波器，雖熱每級濾波器的代碼都是直接型濾波器，但其中的零極點系數的運算還是需要我們自己修改，而且還有仿真好每級濾波器的輸出是否正常。但是沒辦法，因為IIR濾波器幾乎沒有IP核可以調用，我們也只能手寫了

在進行零極點系數乘積運算的過程中，我們一方面可以調用乘法器來進行運算，另一方面可以利用移位的方式進行乘法運算

例如上圖，474可以分解成幾個2的整數次冪的形式的累加形式，因此，可以通過移位的方式實現乘法運算

采用級聯方式實現FPGA的過程要注意的是每級濾波器的輸出位數，保證每級濾波器的輸出數據沒有溢出，其他地方都跟直接型類似

至于采用流水線結構實現級聯結構，就是在每級濾波器的輸出部分加一個寄存器，每來一個時鐘將數據輸出，這一點很簡單了，想必能看到這里的朋友對FPGA這點技巧還是很了解的。

下面是modelsim仿真輸出的各級濾波器的波形，與matlab仿真結果相比幾乎相同，證明我們的結果是正確的

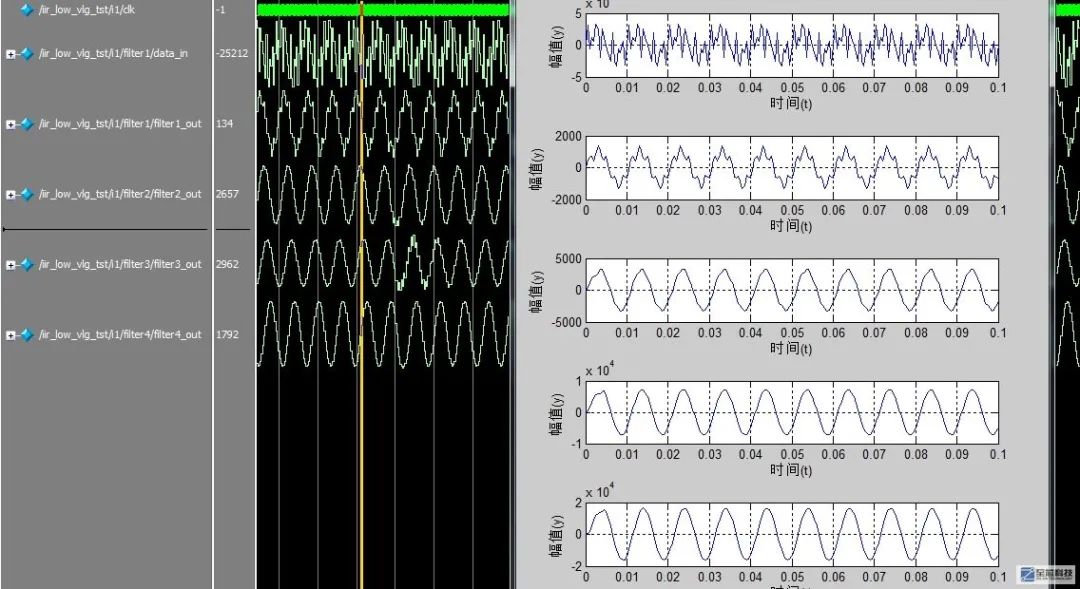
原文標題：零基礎學FPGA（三十） IIR數字濾波器的FPGA實現筆記

文章出處：【微信公眾號：FPGA設計論壇】歡迎添加關注！文章轉載請注明出處。

責任編輯：haq