在FPGA系統(tǒng)中有兩個基本準則非常重要，分別為：數(shù)字表示法和代數(shù)運算的實現(xiàn)。本博文主要介紹數(shù)字表示。

可以購買相關(guān)書籍進行研讀。

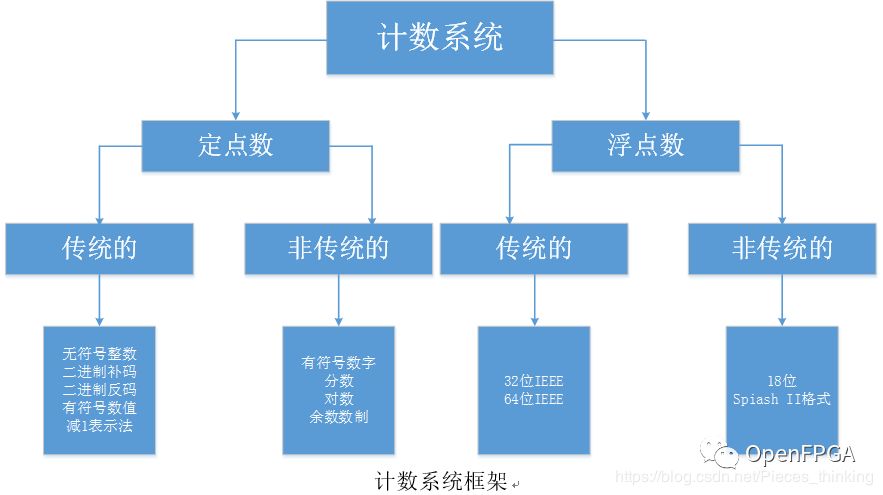
零、計數(shù)系統(tǒng)框架

一 、整數(shù)的表示

數(shù)字信號處理中需要考慮的基本要點是數(shù)字的表示，數(shù)字信號處理需要將量值用有限精度的數(shù)字表示。一方面，該表示必須足夠準確地處理數(shù)字信號處理系統(tǒng)中真實世界的輸入和輸出；另一方面， 該表示必須在硬件實現(xiàn)方面具有高效性。

二進制數(shù)的使用是任何數(shù)字系統(tǒng)的基礎(chǔ)， 當處理大型復(fù)雜的 DSP 系統(tǒng)時， 每秒將需要處理數(shù)十億次的乘加運算。因此， 通過減少位數(shù)來降低硬件開銷的方法將變得非常有意義。

假設(shè)有一個使用 16 位分辨率運算的 DSP 濾波應(yīng)用， 因此對于一個 16 位乘 16 位并行乘法 ， 硬件開銷的量級為 16 X 16 = 256 個單元。使用 16 位字長的原因是它就是 DSP處理器通常使用的字長， 鑒于習(xí)慣仍然選擇一樣的字長。在 FPGA世界中可以選擇分辨率。因此， 如果說 9 位分辨率已經(jīng)足夠了， 乘法器的硬件開銷即為 9 X 9= 81 個單元。這大約是使用 16 位計算開銷的 30%。

因此正確選擇字長很重要：使用太多位浪費硬件資源， 而太少則會損失分辨率。所以， 保證選擇正確的字長的前提是掌握算法和 DSP 知識。

1.1 二進制反碼

可使用二進制反碼描述正數(shù)和負數(shù)。求一個數(shù)的反碼只需對所有的位取反。然而需要注意， 當使用反碼時， 有兩種表示數(shù)字 0 的方法， 通常來說， 用反碼并不能直接表示算術(shù)運算。

當在這種數(shù)字系統(tǒng)中執(zhí)行二進制運算時， 將遇到奇怪的問題， 這是由于數(shù)字 0 有兩個表示版本。事實上，-0 小于+0，這是由于使用反碼表示時：-0+ 1 =+0;+0 -1=-0。

實現(xiàn)上述功能需要相當復(fù)雜的硬件。實際需要的是這樣一種系統(tǒng)， 其處理正數(shù)和負數(shù)與處理無符號數(shù)字一樣， 不需要增加硬件的復(fù)雜性。

反碼實際上從來沒有在實時 DSP 或數(shù)字系統(tǒng)中使用過， 但是它能夠引出標準形式的二進制補碼的概念。

1.2 二進制補碼

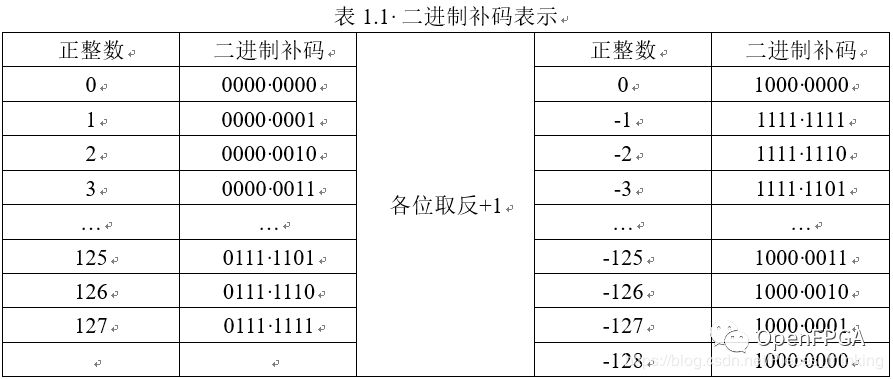
對于+0 和-0 來說， 更加合理的數(shù)字系統(tǒng)為只有一個 0 的二進制補碼。表 1.1 給出了二進制補碼的表示。

生成 0 的第 9 位可被忽略， 注意用二進制補碼可以表示- 128，但不能表示+ 128。在對正值取反時， 會發(fā)現(xiàn)需要用第 9 位表示負零。然而， 如果簡單地忽略這個第 9 位 ， 那么這個負零與正零的表示將完全相同。

注意在數(shù)值系統(tǒng)中， 每個位置上階的意義。例如對于十進制 156 來說：

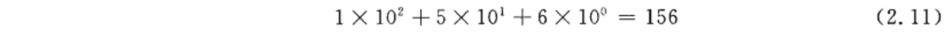
也就是說字符串“156”代表數(shù)字 156，它是每個位置上的值與其階的乘積的和。

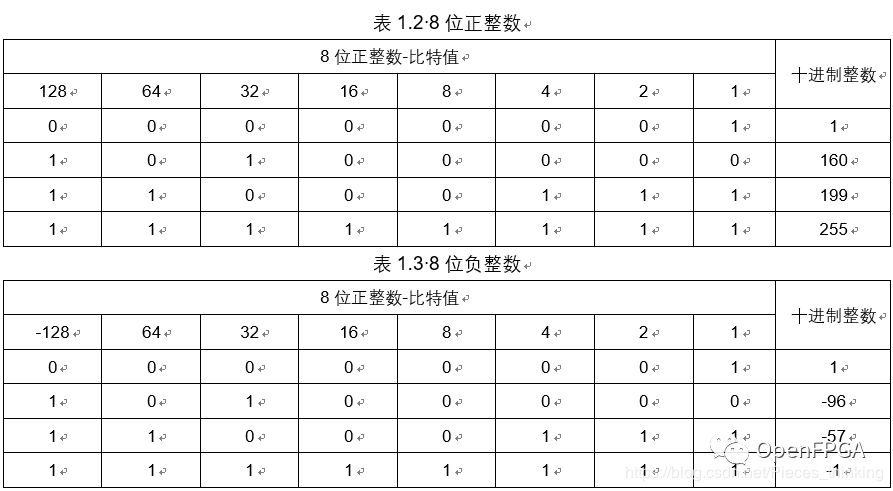
如表1.2 所示， 這個規(guī)則對二進制數(shù)也同樣適用。如表 1.3 所示， 對于二進制補碼整數(shù)， 如果將最左列考慮為負值， 則結(jié)果同樣適。

二、 非整數(shù)值的表示

在數(shù)字信號處理系統(tǒng)中， 經(jīng)常希望描述諸如正弦波的信號， 顯然需要處理非整數(shù)數(shù)值的情況。對這種非整數(shù)值要求的一種可能的解決辦法是允許正弦波幅度按比例增加并以整數(shù)形式來表示。

這種方法很常見， 但在某些情況下， 需要表示 0~1 之間的數(shù)值， 也需要表示整數(shù)之間的數(shù)值。用十進制表示小數(shù)很容易。通過引入十進制小數(shù)點來描述非整數(shù)， 并在小數(shù)點的右邊插人數(shù)字。例如：

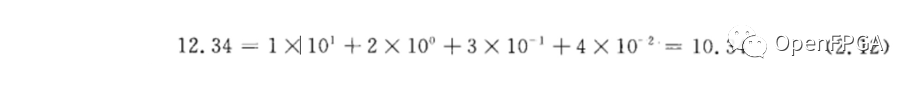
在式中， 字符串“10.34”代表數(shù)字 10. 34 ，即 10 的乘方的倍數(shù)的總和。

同樣地， 可以對二進制數(shù)執(zhí)行同樣的運算：

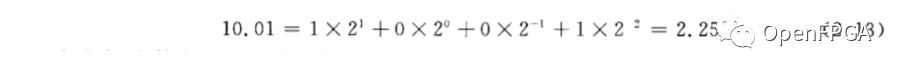
在式屮， 字符串“10.01”表示數(shù)字 2.25，即 2 的乘方的倍數(shù)的總和。

2.1 定點二進制數(shù)

定點數(shù)就是二進制小數(shù)點在固定位罝的數(shù)。二進制小數(shù)點左邊部分的位被定義為整數(shù)位， 而該點右邊部分的位被定義成小數(shù)位。舉例來說：“101.01011”有 3 個整數(shù)位， 5個小數(shù)位。如表 2.1 所示， 定點數(shù)按類似的方式處理有符號整數(shù)。

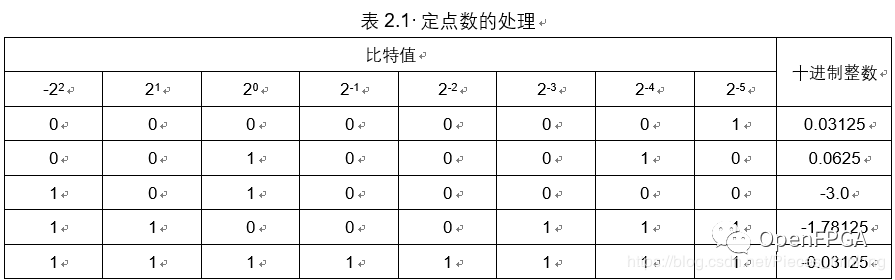
根據(jù)表 2.1可得， 110.00111（ 二進制數(shù)） = - 1.78125（ 十進制數(shù)）

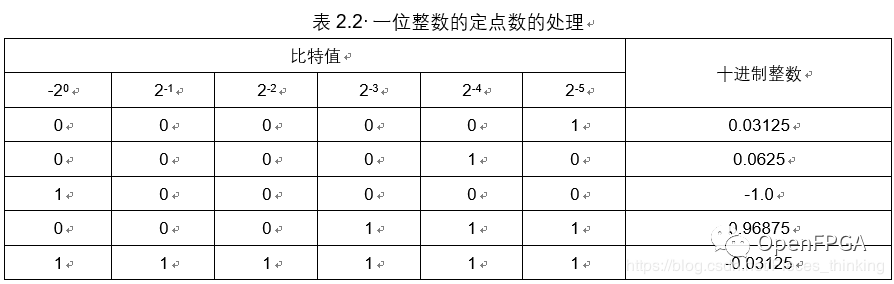
如表 2.2所示 ， 一種非常重要的定點數(shù)字類型只有一個整數(shù)位。

例如， Motorola StarCore 和 TI C62x DSP 處理器都使用只有一個整數(shù)位的定點表示法。這種格式可能是有問題的， 因為它不能表示+ 1.0，實際上， 任何定點格式都不能表示其負數(shù)最小值的相反數(shù)。

所以在使用定點數(shù)時要多加注意。一些 DSP 處理器結(jié)構(gòu)允許利用擴展位對格式進行 1 個整數(shù)位的擴展（ 這些擴展位就是附加的整數(shù)位）。

2.2 定點量化

重新考慮數(shù)字的格式：aaa. bbbb 表示 3 個整數(shù)位， 5 個小數(shù)位。可以表示- 4 和3.96785 之間的數(shù)， 數(shù)之間的步長為 0.03125。由于具有 8 位， 故具有 28 = 256 個不同的值。需要注意使用定點時的量化，將有± 1 /2LSB（ 最低有效位） 的誤差。

量化就是使用有限數(shù)位來表示無限精度的數(shù)。在十進制中， 很熟悉處理給定位數(shù)的十進制小數(shù)的方法。實數(shù)可以表示為 3.14159265… ， 可以量化或?qū)⑵浔硎鰹閹?4 個十進制位的小數(shù) 3.1416。如果在這里使用舍人， 則誤差為：

3.14159265…- 3.1416 =- 0.00000735

如果使用截斷法（ 即第 4 位小數(shù)以后的位數(shù)被扔掉） ， 則誤差將變得更大， 如下：

3.14159265…- 3.1415 = 0.00009265

很明顯， 舍人是比較合適的能夠得到預(yù)期精度的方法。然而該方法也會有一些硬件開銷。盡管開銷相對較小， 但它的確不是免費的。

當乘以小數(shù)時需要處理到給定數(shù)目的位數(shù)。例如， 如果需要計算兩個十進制小數(shù)位， 則計算過程如下：

0.57 X 0.43 = 0.2451

可被舍人到 0.25，或者截斷到 0.24。結(jié)果是不同的。

一旦開始在數(shù)字信號處理系統(tǒng)中執(zhí)行上億次的乘加運算， 就不難發(fā)現(xiàn)這些微小的誤差會因為累積而造成嚴重的影響。

2.3歸一化處理

使川二進制小數(shù)使得算術(shù)運算變得容易， 也易于處理字長增長。作為一個例子， 考這樣一個“ 機器”， 它有 4 位十進制數(shù)和一個具有 4 個數(shù)字位的算術(shù)單元， 范圍為-9999~+9999。兩個 4 位數(shù)相乘將導(dǎo)致多達 8 個有效數(shù)字。

6787 X 4198 = 28491826 --》（標定）2849.1826–》（截斷）2849

如果想把這個數(shù)送到該機器的下一級（ 算術(shù)運算具有 4 位的精度 ） ， 那么需要按比例減小 10000 倍， 然后截斷 。

將其歸一化到范圍-0.9999 ~+0.9999。

0.6787 X 0.4198 = 0.28491826 —》（截斷） 0.2849

現(xiàn)在截斷到 4 位的操作變得相當容易。當然兩種結(jié)果是嚴格一致的， 而差別僅僅在于如何執(zhí)行截斷和標定。

然而對輸入執(zhí)行歸一化操作， 所有的輸人值都位于-1~ + 1 的區(qū)間內(nèi)。可以注意到該區(qū)間內(nèi)任意兩個數(shù)的乘積同樣存在于-1 +1 的區(qū)間之內(nèi)。

同樣的歸一化操作也適用于二進制， 而且大多數(shù)數(shù)字信號處理系統(tǒng)也使用二進制點。

下面考慮 二 進 制 補 碼 中 的 8 位 數(shù) 值。因 此 該 數(shù) 值 的 取 值 范 圍 是 10 0 0 0 0 0 0~01111111 （-128~+127）。

如果將這些數(shù)歸一化到-1~ 1 之間（ 除以 128 ）， 那么二進制的范圍是 1.0000000~0.1111111（ -1~ 0.9921875，其中 127/128= 0.9921875 ）。所以把十進制乘法中歸一化的概念用于二進制。

十進制乘法 36 X 97=3492 等價于二進制乘法 0010 0100 X 0110 0001 = 0000 1101 1010010。在二進制中，將值歸一化就是計算 0.0100100 X 0.1100001 =0.00110110100100。等價于十進制中：

0.28125 X 0.7578125=0.213134765625

注意：在 數(shù) 字 信 號 處 理 系 統(tǒng) 中， 在 設(shè) 計 者 的 眼 中， 二 進 制 點 是 存 在 的， 然 而 卻 沒 有 實際 的 連 接 或 連 線。這 只 是 使 得 跟 蹤 字 長 增 長， 以 及 通 過 扔 掉 小 數(shù) 位 來 截 斷 變 得 更 加 容易。當 然 如 果 更 愿 意 使 用 整 數(shù) 并 且 跟 蹤 定 標 等 ， 也 可 以 這 樣 做。得 到 的 答 案 是 相 同 的 ，硬 件 開 銷 也 是 相 同 的。

2.4 小數(shù)部分截斷

二進制中， 截斷是簡單地將位去除的過程。通常使用這種強制的方法來將大的二進制字長變小， 通常需要截掉最低有效位 （LSB），該操作的影響是降低了準確度。

考慮將十進制數(shù) 7.8 9 9 2 截 斷 到 3 個 有 效 位 7.89。當然， 可以截斷最低有效位 ， 其結(jié)果是損失了精度（ 分辨率） ， 但它仍是最初 5 位數(shù)的代表。如果截斷最高有效位 992 （ 或0.0992）， 其結(jié)果將不是所希望的， 而且也失去了意義。

在二進制中， 最髙有效位截斷的概念是很少使用的， 在十進制的例子中， 最高有效位截斷通常是災(zāi)難性的。然而， 在某些極少情況下， 一系列的操作將導(dǎo)致整個數(shù)值的范圍減小。所以移除 MSB 也是有好處的。

截斷 MSB 通常發(fā)生在要截斷的位為空的時候。當使用有符號的值時， 由于丟失了符號位， 截斷 MSB 將會帶來問題。

舍入是一種更準確的方法， 但同時也是更復(fù)雜的技術(shù)。該技術(shù)需要進行一個加法操作， 然后再直接截斷，該過程等價于十進制的四舍五人， 即通過在 7 。 8 9 上 加 0 。 0 5 然 后 再 截 斷 到 7.9 來 舍人到一個小數(shù)位。因此簡單的舍人需要一個加法操作。

2.5 一種不同的方法 Trounding

Trounding 是截斷 truncation ）和 舍 人（ rounding ）之 間 的 一 種 折中方 法， 其 特 點如下。

① 和舍人一樣， Trcnmding 保留了 LSB 以上的信息。

② 它和舍人不同， 它不影響新的 LSB 以上的任何位。

其具體實現(xiàn)方法在 XtremDSP 中進行了詳細的介紹， 具體可以參看這部分相關(guān)內(nèi)容。Trounding 的好處是它不需要全加器， 而且可以通過或門得到比截斷更好的性能。盡管是一個很小的優(yōu)點， 但這種成本上的節(jié)省以及性能的改善還是有價值的。

三、 浮點數(shù)定義及表示

3.1 標 準 浮 點 數(shù) 表 述

浮點數(shù)可以在更大的動態(tài)范圍內(nèi)提供更高的分辨率， 通常當定點數(shù)由于受其精度和動態(tài)范圍所限不能勝任時， 浮點數(shù)能提供解決方案。當然， 也在速度和復(fù)雜度方面帶來了損失 ， 大多數(shù)的浮點數(shù)都遵循單精度或雙精度的 IEEE 浮點標準。標準浮點數(shù)字長由一個符號位 S，指數(shù) e 和無符號（ 小數(shù)） 的規(guī)格化尾數(shù)m構(gòu)成， 其格式如下：

浮點數(shù)可以用下式描述：

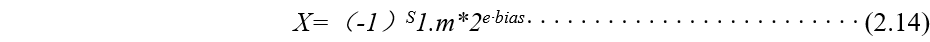
指數(shù) e=1…2 是為∞準備的。而 e=0 是 為 0 預(yù) 備 的。表 2.3 給 出 了 IEEE 的單精度和雙精度格式的參數(shù)。

在浮點乘法中， 尾數(shù)部分可以像定點數(shù)一樣相乘， 而把指數(shù)部分相加。浮點數(shù)減法復(fù)雜一些，因為首先將尾數(shù)歸一化， 就是將兩個數(shù)都調(diào)整到較大的指數(shù)， 然后將兩個尾數(shù)相加。對于加法和乘法混合運算來說， 最終的歸一化， 就是將結(jié)果尾數(shù)再統(tǒng)一乘小數(shù)1.m 形式的表達式， 這是非常必要的。

一些浮點編碼的范例 （ 單精度浮點 32 位， 注意這些運算都是基于二進制的計算）。如下：

注意小數(shù)點之前的 1 沒有被編碼（ 那里一直有個 1， 因而不需要顯式表示）。

3.2 浮點數(shù)的短指數(shù)表示

簡化浮點硬件的一種方法是創(chuàng)建一種使用短指數(shù)的數(shù)據(jù)格式。這種情況下有一個 4位的指數(shù)和一個 11 位的尾數(shù)。因此可以表示-7~ 8 的范圍內(nèi)的指數(shù)。其結(jié)果在動態(tài)范圍內(nèi)顯著地增加， 代價只是精度輕微降低。表 2.4 給出了定點數(shù)和短指數(shù)的比較。

3.3 浮點數(shù)的應(yīng)用

浮點在許多具有專用浮點單元（ FPU ） 的 DSP 處理器中被廣泛使用。不在 FPGA中使用浮點的原因如下。

① 運算速度慢：FPU 是一個復(fù)雜的單元， 設(shè)計中的每個代數(shù)運算將共用該單元。

② 低效的芯片面積：使用 FPGA 實現(xiàn) FPU 需要很大的硬件空間。

然而， 某些情況下 FPU 也許是必不可少的， 例如在需要一個巨大的動態(tài)范圍的應(yīng)用場合， 使用浮點可能使得設(shè)計更加簡單 ， 這是因為在定點設(shè)計中， 需要最好地利用可用的動態(tài)范圍， 但是在浮點設(shè)計中， 動態(tài)范圍的限制不是一個需要考慮的問題。

原文標題：基于 FPGA 的數(shù)字表示

文章出處：【微信公眾號：OpenFPGA】歡迎添加關(guān)注！文章轉(zhuǎn)載請注明出處。

責(zé)任編輯：haq