什么是GCN
由于高度的復雜性和信息的結構特征,圖上的機器學習是一項困難的任務。「GCN是被設計用來針對圖結構的神經網絡,它能從之前的網絡層中聚合信息。在圖中,這種機制能夠對節點產生有用的特征表示。」
GCN是基于圖機器學習的非常強大的神經網絡體系結構。
實際上,它們是如此強大,以至于隨機發起的2層GCN都可以產生網絡中節點的有用特征表示。
下圖說明了由此類GCN生成的網絡中每個節點的二維表示。請注意,即使沒有任何訓練,網絡中節點的相對接近度仍保留在二維表示中。
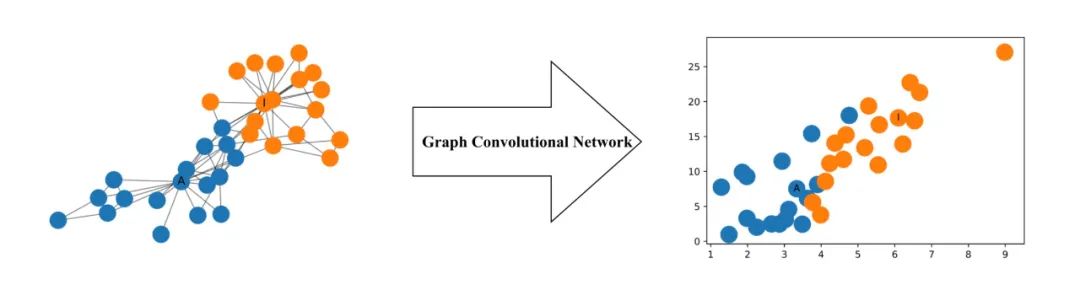
更正式地說,圖卷積網絡(GCN)是在圖上運行的神經網絡。給定圖G =(V,E),V表示節點,E表示邊,則GCN作為輸入
輸入特征矩陣X(N×F?),其中N是節點數,F?是每個節點的輸入特征數,以及圖結構的N×N矩陣表示形式,例如G的鄰接矩陣A
因此,GCN中的隱藏層可以寫成H?= f(H??1,A))。
其中H?= X,f是傳播(propagation)方式。每一層H?對應于一個N×Fi特征矩陣,其中每一行是一個節點的特征表示。在每一層,使用傳播規則f聚合這些特征,以形成下一層的特征。這樣,特征在連續層上變得越來越抽象。在此框架中,GCN的變體僅在傳播規則f的選擇上有所不同。
一個簡單的傳播規則
傳播規則中最簡單的一種是:
f(H?,A)=σ(AH?W?)
其中W?是第i層的權重矩陣,而σ是非線性激活函數,例如ReLU函數。權重矩陣的尺寸為F?×F??1;換句話說,權重矩陣的第二維的大小確定了下一層的特征數量。如果你熟悉卷積神經網絡,則此操作類似于過濾操作(filtering operation),因為這些權重在圖中的節點之間共享。
簡化
讓我們從最簡單的角度檢查傳播規則:
i = 1,滿足 f是輸入特征矩陣的函數
σ是恒等函數
選擇權重 AH?W?=AXW?= AX
換句話說,f(X,A)= AX。這個傳播規則可能有點太簡單了,稍后我們會添加缺失的部分。AX現在等效于多層感知器的輸入層。
一個簡單的圖形示例
舉一個簡單的例子,我們使用以下圖形:
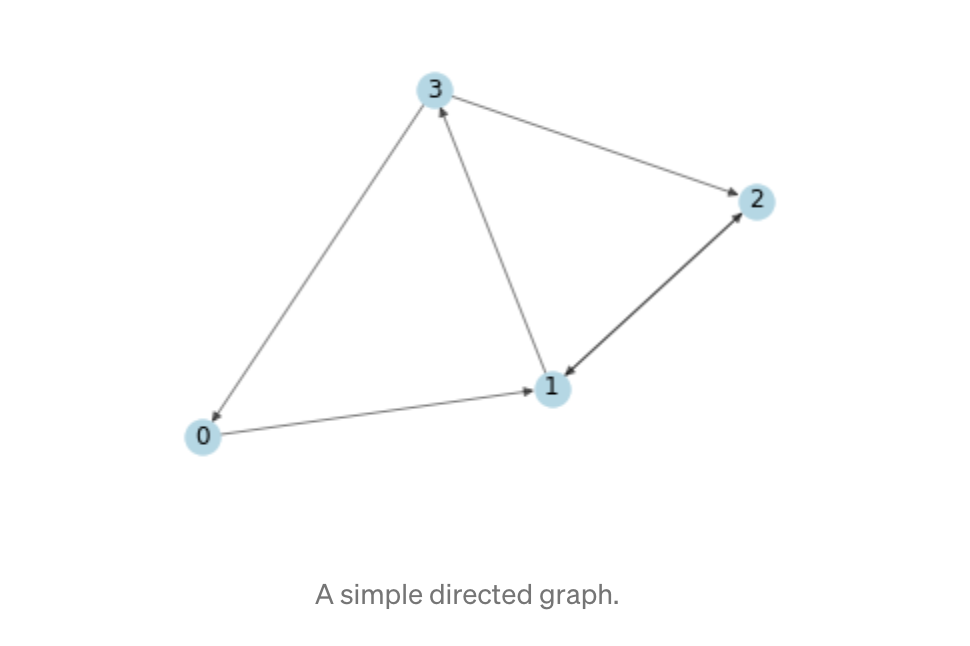
下面是其numpy鄰接矩陣表示形式。
A = np.matrix([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]],
dtype=float
)
接下來,根據其索引為每個節點生成2個整數特征,便于以后手動確認矩陣計算。
In [3]: X = np.matrix([
[i, -i]
for i in range(A.shape[0])
], dtype=float)
X
Out[3]: matrix([
[ 0., 0.],
[ 1., -1.],
[ 2., -2.],
[ 3., -3.]
])
應用傳播規則
好吧!現在,我們有了一個圖形,其鄰接矩陣A和一組輸入要素X。讓我們看看應用傳播規則時會發生什么:
In [6]: A * X
Out[6]: matrix([
[ 1., -1.],
[ 5., -5.],
[ 1., -1.],
[ 2., -2.]]
發生了什么?現在,每個節點(每行)的表示形式都是其鄰居特征的總和!換句話說,圖卷積層將每個節點表示為其鄰居的集合。注意,在這種情況下,如果存在從v到n的邊,則節點n是節點v的鄰居。
問題
你可能已經發現了問題:
節點的匯總表示不包括其自身的功能!
該表示是鄰居節點特征的集合,因此只有具有自環的節點才會在集合中包括自己的特征。度數較大的節點的特征將具有較大的值,而度數較小的節點將具有較小的值。這可能會導致梯度消失或爆炸,但對于隨機梯度下降算法(通常用于訓練此類網絡并且對每個輸入特征的比例(或值的范圍)敏感)也存在問題。在下文中,我將分別討論每個問題。
添加自環
為了解決第一個問題,可以簡單地向每個節點添加一個自環。實際上,這是通過在應用傳播規則之前將單位矩陣I與鄰接矩陣A相加來完成的。
In [4]: I = np.matrix(np.eye(A.shape[0]))
IOut[4]: matrix([
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]
])
In [8]: A_hat = A + I
A_hat * X
Out[8]: matrix([
[ 1., -1.],
[ 6., -6.],
[ 3., -3.],
[ 5., -5.]])
由于該節點現在是其自身的鄰居,因此在總結其鄰居的特征時會包括該節點自己的特征!
規范特征表示
通過將鄰接矩陣A與D的逆矩陣相乘來變換鄰接矩陣A,可以按節點度對特征表示進行歸一化。因此,我們簡化的傳播規則如下所示:
f(X,A)=D?1AX
讓我們看看發生了什么。我們首先計算度矩陣。
In [9]: D = np.array(np.sum(A, axis=0))[0]
D = np.matrix(np.diag(D))
D
Out[9]: matrix([
[1., 0., 0., 0.],
[0., 2., 0., 0.],
[0., 0., 2., 0.],
[0., 0., 0., 1.]
])
在應用規則之前,讓我們看看對鄰接矩陣進行轉換后會發生什么。
Berfore
A = np.matrix([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]],
dtype=float
)
After
In [10]: D**-1 * A
Out[10]: matrix([
[0. , 1. , 0. , 0. ],
[0. , 0. , 0.5, 0.5],
[0. , 0.5, 0. , 0. ],
[0.5, 0. , 0.5, 0. ]
])
請注意,鄰接矩陣每一行中的權重(值)已除以與該行相對應的節點的度。我們將傳播規則與變換后的鄰接矩陣一起應用:
In [11]: D**-1 * A * X
Out[11]: matrix([
[ 1. , -1. ],
[ 2.5, -2.5],
[ 0.5, -0.5],
[ 2. , -2. ]
])
得到與相鄰節點特征均值相對應的節點表示。這是因為(轉換后的)鄰接矩陣權重,與相鄰節點特征加權和的權重相對應。我鼓勵你自己驗證此觀察。
放在一起
現在,我們結合了自循環和標準化技巧。此外,我們將重新介紹先前為簡化討論而丟棄的權重和激活函數。
加重權重
首要任務是應用權重。請注意,這里D_hat是A_hat = A + I的度矩陣,即具有強制自環的A的度矩陣。
In [45]: W = np.matrix([
[1, -1],
[-1, 1]
])
D_hat**-1 * A_hat * X * W
Out[45]: matrix([
[ 1., -1.],
[ 4., -4.],
[ 2., -2.],
[ 5., -5.]
])
如果我們想減小輸出特征表示的維數,可以減小權重矩陣W的大小:
In [46]: W = np.matrix([
[1],
[-1]
])
D_hat**-1 * A_hat * X * W
Out[46]: matrix([[1.],
[4.],
[2.],
添加激活功能
我們選擇保留特征表示的維數并應用ReLU激活功能。
In [51]: W = np.matrix([
[1, -1],
[-1, 1]
])
relu(D_hat**-1 * A_hat * X * W)
Out[51]: matrix([[1., 0.],
[4., 0.],
[2., 0.],
[5., 0.]])
瞧!具有鄰接矩陣,輸入函數,權重和激活功能的完整隱藏層!
簡單樣例
最后,我們可以在真實圖上應用圖卷積網絡。我將向你展示如何產生我們在文章開頭看到的要素表示。
扎卡里的空手道俱樂部
扎卡里(Zachary)的空手道俱樂部是一種常用的社交網絡,其中節點代表空手道俱樂部的成員,其邊緣相互聯系。當扎卡里(Zachary)研究空手道俱樂部時,管理者與教練之間發生了沖突,導致俱樂部分裂為兩部分。下圖顯示了網絡的圖形表示,并且根據俱樂部的哪個部分標記了節點。管理員和講師分別標有“ A”和“ I”。
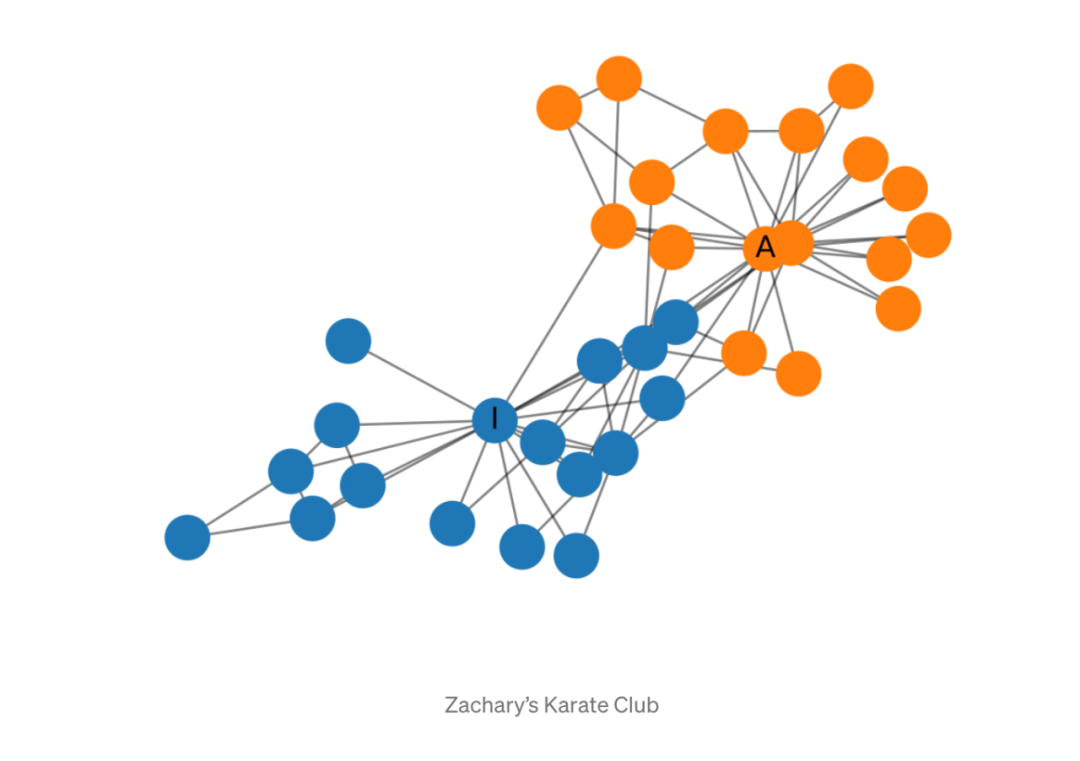
建立GCN
現在來建立圖卷積網絡。實際上我們不會訓練網絡,只是簡單地隨機初始化,以產生在本文開頭看到的功能表示。我們將使用圖網絡networkx表示整個圖,并計算A_hat和D_hat矩陣。
from networkx import karate_club_graph, to_numpy_matrixzkc = karate_club_graph()
order = sorted(list(zkc.nodes()))A = to_numpy_matrix(zkc, nodelist=order)
I = np.eye(zkc.number_of_nodes())A_hat = A + I
D_hat = np.array(np.sum(A_hat, axis=0))[0]
D_hat = np.matrix(np.diag(D_hat))
接下來,我們隨機初始化權重。
W_1 = np.random.normal(
loc=0, scale=1, size=(zkc.number_of_nodes(), 4))
W_2 = np.random.normal(
loc=0, size=(W_1.shape[1], 2))
堆疊GCN層:在這里,我們僅使用單位矩陣作為特征表示,即,每個節點都表示為單次熱編碼的分類變量。
def gcn_layer(A_hat, D_hat, X, W):
return relu(D_hat**-1 * A_hat * X * W)H_1 = gcn_layer(A_hat, D_hat, I, W_1)
H_2 = gcn_layer(A_hat, D_hat, H_1, W_2)
output = H_2
提取特征表示:
feature_representations = {
node: np.array(output)[node]
for node in zkc.nodes()}
瞧!特征表示很好地將Zachary空手道俱樂部中的社區分隔開來。而且我們還沒有開始訓練!
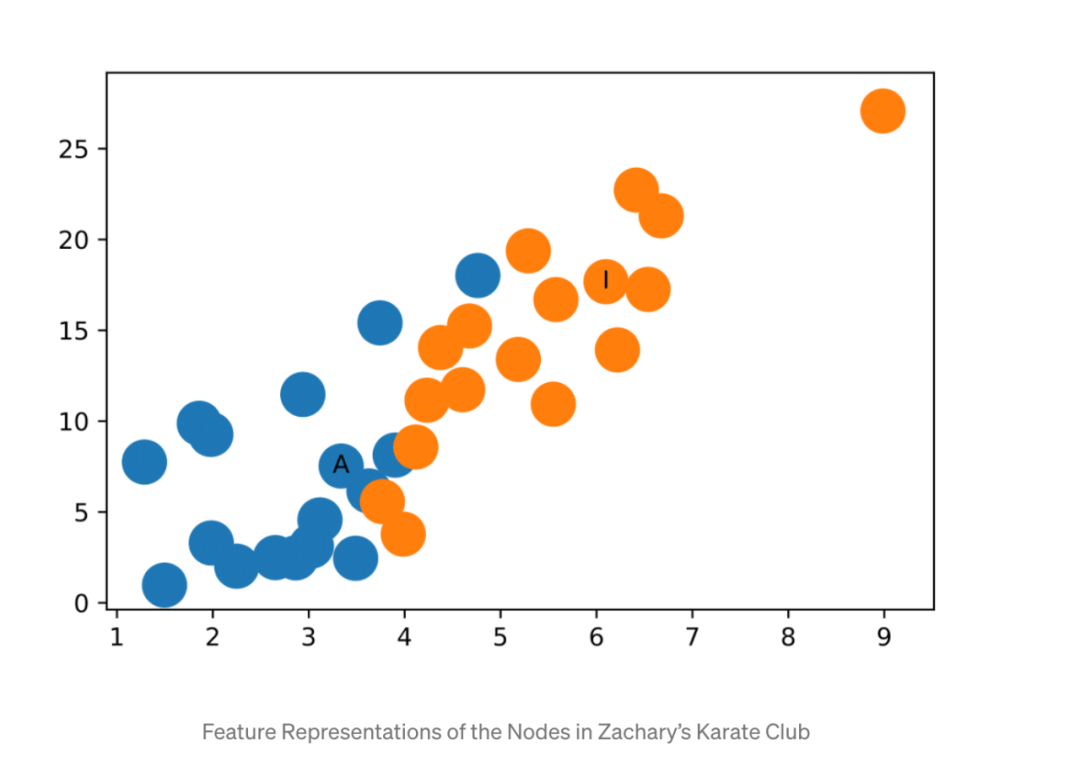
對于此示例,由于ReLU函數的作用,隨機初始化的權重很有可能在x軸或y軸上給出0值,因此需要進行幾次隨機初始化才能產生上圖。
結論在這篇文章中,我對圖卷積網絡進行了高級介紹,并說明了GCN中每一層節點的特征表示是如何基于其鄰域聚合而得出的。我們了解了如何使用numpy構建這些網絡以及它們的強大功能:即使是隨機初始化的GCN,也可以在Zachary的空手道俱樂部中分離社區。
編輯:lyn
-
機器學習
+關注
關注
66文章
8406瀏覽量
132566 -
GNN
+關注
關注
1文章
31瀏覽量
6335 -
GCN
+關注
關注
0文章
5瀏覽量
2284
原文標題:【GCN】2021年,我終于決定入門GCN
文章出處:【微信號:zenRRan,微信公眾號:深度學習自然語言處理】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
硬件工程師入門的基礎元器件知識





 關于GCN的入門學習知識詳解
關于GCN的入門學習知識詳解













評論