今天想談的問題是：什么是貝葉斯優化/Bayesian Optimization，基本用法是什么？

本文的定位是：幫助未接觸、僅聽說過、初次接觸貝葉斯優化的小白們一文看懂什么是貝葉斯優化和基本用法，大神/貝葉斯優化專家們求輕噴，覺得不錯的記得幫點贊/在看/轉發幫擴散哦！謝謝。

梳理這個問題有這么兩個原因：

1、在工業界，最近我看到不少同學在探索并使用貝葉斯優化的方法尋找更好的超參，找到performance更好的模型，漲點漲分；

2、家里另一位在學習和研究“Safety”強化學習的時候，發現一個“牛牛“的代碼是基于貝葉斯優化的，為了提高家庭地位不得不看一看啦哈哈哈。

于是之前僅僅只聽說過貝葉斯優化的我，趕緊知乎治學，面向Github編程，面向谷歌解決問題，一通搜索學習了解入門之后基本有個框架和概念了，遂記錄在此，望茫茫互聯網看到這個文章的小白們也可以快速入門貝葉斯優化/Bayesian Optimization！

貝葉斯優化應用場景

如果你要 解決的問題/面對的場景，假設輸入為x，輸出為f（x），有如下特點，那不妨試一下貝葉斯優化吧。

這個函數f（x）特點是計算量特別大，每次計算都特別耗時、耗資源；

甚至f（x）可能都沒有解析式表達式。

無法知道函數f（x）對于x的梯度應該如何計算。

需要找到函數f（x）在x自變量上的全局最優解（最低點對應的取值）

舉例：

我們有一個參數量巨大的推薦系統模型（或者是某個NLP模型），每次訓練很消耗資源和時間，但我們仍然期待找到更好的模型超參數讓這個推薦系統的效果更好，而人工參數搜索太費神、Grid Search太消耗資源和時間，想找一個不那么費神同時資源消耗和時間消耗也比Grid Search稍微小一點的辦法。

這個場景基本滿足以上特點：一是計算量大、二是模型對于超參數（比如learning rate學習率，batch size）的梯度無從知曉；所以可以考慮用貝葉斯優化來尋找最合適的一組超參。對此實際應用感興趣的同學可以進一步閱讀：Facebook efficient-tuning-of-online-systems-using-bayesian-optimization。

但這兒還是要給想用貝葉斯優化尋找超參的同學稍微潑以下冷水：由于實際系統的復雜性、計算量超級巨大（或者說資源的限制），可能連貝葉斯優化所需要的超參組合都無法滿足，導致最后超參搜索的結果不如一開始拍腦袋（根據經驗的調參）效果好哦。所以這是一個辦法，但最好不是唯一辦法哦。

一個關于Safe RL的例子：強化學習中的一個環境里有Agent A（比如一個小學生學如何騎自行車）在學習如何根據環境做出action，同時又有一個Agent B在幫助Agent A進行學習（比如有個老師擔心寶貝學生摔倒，要教學生騎車）。Agent B需要從多種策略（每個策略還有一些參數）里找到一個最優的策略組合幫助Agent A進行學習（比如學自行車的時候自行車旁邊放個2輪子、帶個頭盔，或者直接用手扶著，或者直接推著推著突然放手）。那么Agent B的如何選擇最優輔助策略組合以及對應策略的參數也可以使用貝葉斯優化。感興趣的同學可以閱讀NeurIPS 2020的Spotlight presentation文章：Safe Reinforcement Learning via Curriculum Induction。

圖1 Safe RL中例子

有了使用場景，我們就會問什么是貝葉斯優化啦。

什么是貝葉斯優化

貝葉斯優化定義的一種形象描述。

分享Medium上這個不錯的例子。

比如我們有一個目標函數c（x），代表輸入為x下的代價為c（x）。優化器是無法知道這個c（x）的真實曲線如何的，只能通過部分（有限）的樣本x和對應的c（x）值。假設這個c（x）如圖2所示。

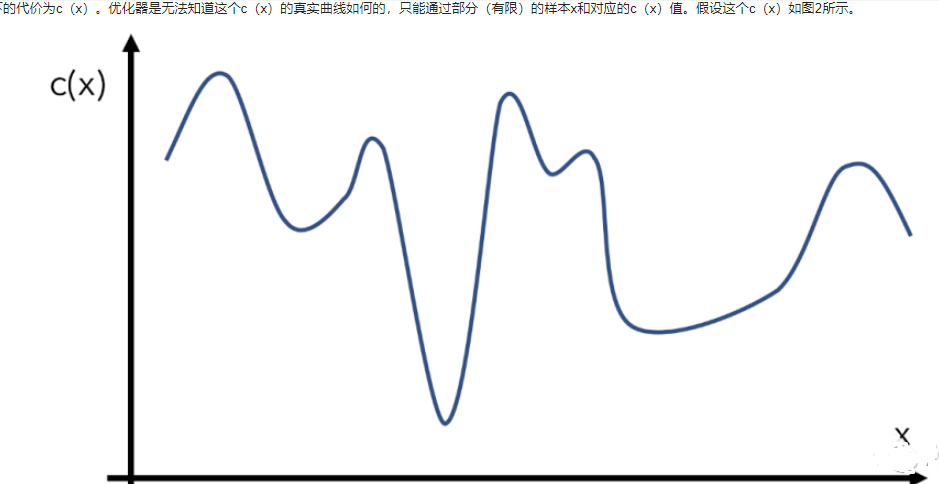
圖2 優化函數舉例

貝葉斯優化器為了得到c（x）的全局最優解，首先要采樣一些點x來觀察c（x）長什么樣子，這個過程又可以叫surrogate optimization（替代優化），由于無法窺見c（x）的全貌，只能通過采樣點來找到一個模擬c（x）的替代曲線，如圖3所示：

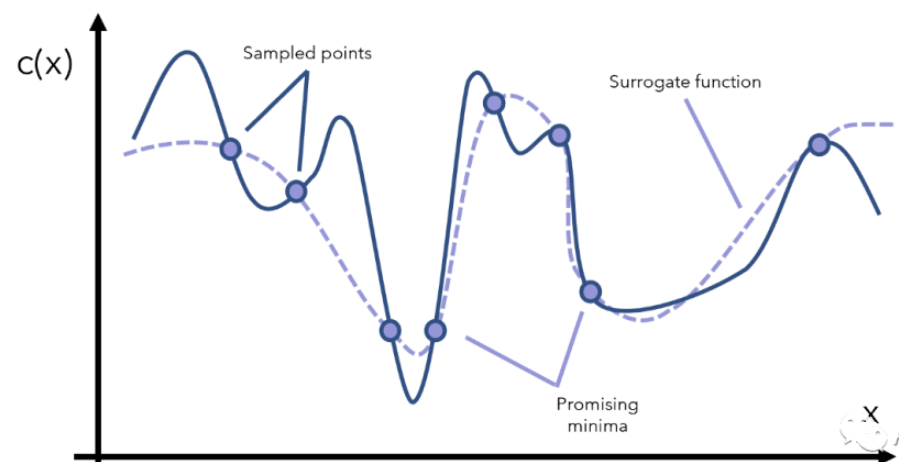
圖3 采樣的點與替代的曲線

得到這個模擬的/替代的曲線之后，我們就能找到兩個還算不錯的最小值對應的點了（圖3中標注的是promising minima），于是根據當前觀察到的這兩個最小點，再采樣更多的點，用更多的點模擬出一個更逼真的c（x）再找最小點的位置，如圖4所示。

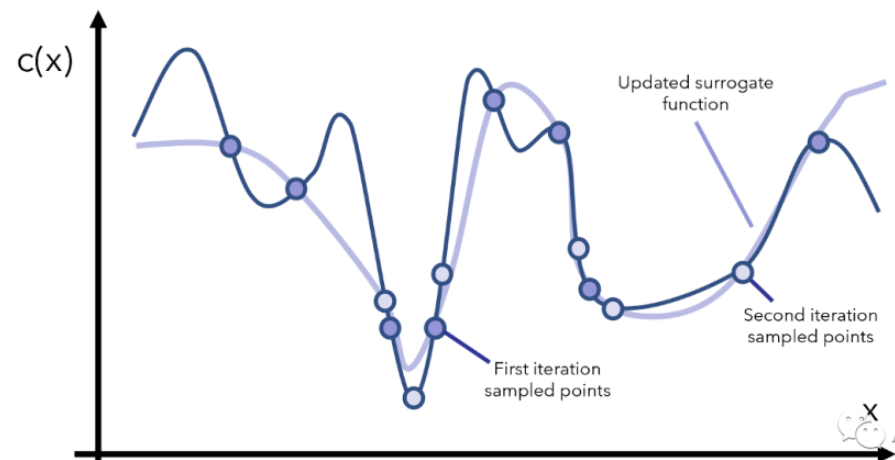
圖4 繼續采樣 空心的圈為第2次采樣的點

然后我們重復上面這個過程，每次重復的時候我們干以下幾件事情：先找到可擬合當前點的一個替代函數，然后根據替代函數的最小值所在的位置去采樣更多的 ，再更新替代函數，如此往復。

函數替代的例子： 給定x的取之范圍，那么一個復雜的函數y = arcsin（（ 1- cos（x） * cos（x）） / sinx） 則可以用y=x來替代。

如果我們的c（x）不是特別奇怪的話，一般來說經過幾次迭代之后，我們就能找到c（x）的最優解啦。當然如果c（x）特別奇怪，那可能是數據的問題而不是。。。c（x）的問題。再回頭來看上面這個過程，貝葉斯優化的厲害的地方：a 幾乎沒有對函數c（x）做任何的假設限定，也不需要知道c（x）的梯度，也不需要知道c（x）到底是個什么解析表達式，就直接得出了c（x）的全局最優。

以上例子中有兩個重要的點：

1、用什么函數作為替代函數（選擇函數進行curve-fiting的過程），對應Gaussian Processes；

2、如何根據當前信息和替代函數的局部最優點繼續采樣x，對應acquisition function。

為什么可以用Gaussian Processes對曲線進行擬合呢？

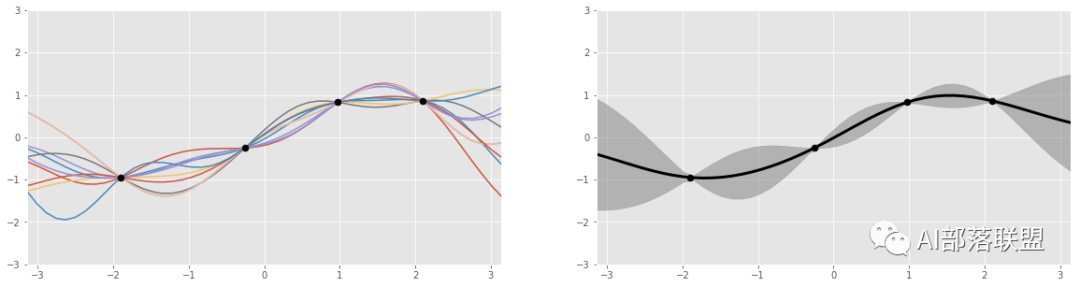
圖5 總共4個黑色的點，代表4個數據點。左邊是Gaussian process產生的多個函數曲線（紅、藍、黃等曲線）；右邊的圖顯示的是左圖的那些函數都會經過黑點，以及函數值的波動范圍（灰色部分）。

Gaussian Processes的一個非常大的優點：“先驗知識”可以根據新觀測量更新，而Gaussian Processes又可以根據這個更新后的“先驗知識”得到新的function的分布，從而更好的擬合數據點。也就是：如果我們觀測了3個函數值，那么有一種高斯分布和這三個觀測的數據點對應，而如果我們觀測了4個點，又可以新計算一個對應的高斯分布。

這里我們簡單以圖6為例描述一下：Gaussian Process是如何根據擬合數據，然后對新的數據做預測？

如圖6所示，假設現已觀測到3個點（左邊黑色的3個圈），假設這計算得到3個函數值分布是 ，Gaussian Process的理論告訴我們（具體理論先略了）給定一個新的 輸入 （左圖藍色 ），我們可以按照圖6左下角的方式計算出與藍色 對應的 的均值和方差，也就是輸出的范圍。

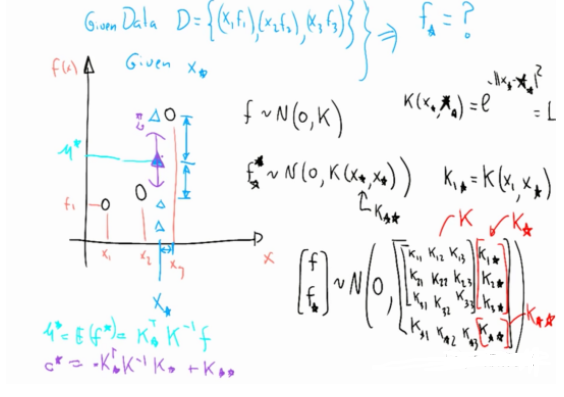
圖6 更新過程示意圖

acquisition function在決定如何選取新的采樣點是面臨兩個經典問題：exploitation和exploration，我稱之為深度和廣度。以圖5的例子來看，

exploitation意味著盡可能順著當前已知的信息，比如順著黑色點的地方來采樣更多的點，也就是深度。當已知信息利用到一定程度，這種exploitation方向的采樣會很少有信息增益。

exploration顧名思義就是更趨向探索性質，比如順著圖5右邊的灰色區域較大的地方探索，也就是廣度，探索更多未知的地方。

假設我們把acquisition functin簡寫為aq（x），整個貝葉斯優化可以概括為：

基于Gaussian Process，初始化替代函數的先驗分布；

根據當前替代函數的先驗分布和aq（x），采樣若干個數據點。

根據采樣的x得到目標函數c（x）的新值。

根據新的數據，更新替代函數的先驗分布。

并開始重復迭代2-4步。

迭代之后，根據當前的Gaussian Process找到全局最優解。

也就是說貝葉適優化實際上是：由于目標函數無法/不太好 優化，那我們找一個替代函數來優化，為了找到當前目標函數的合適替代函數，賦予了替代函數概率分布，然后根據當前已有的先驗知識，使用acquisition function來評估如何選擇新的采樣點（trade-off between exploration and exploitation），獲得新的采樣點之后更新先驗知識，然后繼續迭代找到最合適的替代函數，最終求得全局最優解。

貝葉斯優化偏公式的定義，個人還是更喜歡公式定義的。

Bayesian Optimization（BO）是對black-box函數全局最優求解的一種strategy。具體的 是一個定義在 上L-Lipschitz連續的函數，我們想要找到 的全局最優解：

這里我們假設函數 是一個black-box，對于這個black-box，我們只能觀測到有噪聲的函數值： 其中 ，也就是零均值高斯分布。于是整個優化目標可以變成：找到一系列的 使得 最小：

要讓 被快速優化到最小，由于 對應了函數 這個最小點，所以越靠近 開始采樣，那么采樣得到的一系列 越快結束 的優化，也就結束了 全局最優解的優化。

這一序列 具體是如何得到的呢？假設我們在第 次iteration里采樣到了 ，我們將新觀測到的數據加入到已有的觀測數據 里，然后通過優化一個叫actuisition function 的函數得到下一個時刻要采樣的 ，也就是 。

那么這個 要如何設計呢？歸根結底是如何根據已有的觀測量選擇 ，于是設計過程中就遇到了經典的exploration和exploitation問題，也就是是繼續沿著已有的信息深挖，還是擴大信息的覆蓋廣度？

我們已有的觀測量是 ，假設這些觀測量服從高斯分布 ，其中 分別是均值和方差，也對應著exploitation和exploration（方差通常也指不確定性）。那我們就根據expatiation和exploration來設計 吧，這里只介紹一鐘叫Gaussian Process-Upper Confidence Bound （GP-UCB）的設計：

很容易看出， a 其實就是均值和方差加權和，也就起到了調和exploitation和exploration的作用啦。至于其他幾種acquisition function，Expected Improvement （EI），（Predictive） Entropy Search，Thompson Sampling（TS）等本文就不再一一描述啦。

有了 就能確定新的采樣點了，Gaussian Process也就能跟著更新了，最終替代函數的擬合也就越來越貼近真實函數了，最終找到全局最優點。

結合上面的形象描述和公式定義描述，總結以下貝葉斯優化的兩個重點：

1. 定義一種關于要優化的函數/替代函數的概率分布，這種分布可以根據新獲得的數據進行不斷更新。我們常用的是Gaussian Process。

2. 定義一種acquisition function。這個函數幫助我們根據當前信息決定如何進行新的采樣才能獲得最大的信息增益，并最終找到全局最優。

貝葉斯優化的應用

紙上得來終覺淺，絕知此事要躬行。

我們就用python來跑幾個例子看看吧。以下例子需要安裝Gpy和GpyOpt這兩個python庫。

假設我們的目標函數是：

這個函數定義在［-1，1］之間，通常也叫domain。這個函數的在定義區間的最優點是：x 。于是代碼為：

import GPyOptdef myf（x）： return x ** 2bounds = ［{‘name’： ‘var_1’， ‘type’： ‘continuous’， ‘domain’： （-1，1）}］# 變量名字，連續變量，定義區間是-1到1max_iter = 15# 最大迭代次數myProblem = GPyOpt.methods.BayesianOptimization（myf，bounds）#用貝葉適優化來求解這個函數，函數的約束條件是boundsmyProblem.run_optimization（max_iter）#開始求解print（myProblem.x_opt）#打印最優解對應的x為-0.00103print（myProblem.fx_opt）#打印最優解對應d的函數值為0.0004

總結

本文主要有以下內容：

寫貝葉適優化的出發點。

貝葉適優化的適用場景。

貝葉適優化是什么？（包括一個形象和一個公式化的解釋）。

貝葉適優化的應用例子。

那么問一問自己，看懂了嗎？

參考文獻：

https://zhuanlan.zhihu.com/p/76269142

https://radiant-brushlands-42789.herokuapp.com/towardsdatascience.com/the-beauty-of-bayesian-optimization-explained-in-simple-terms-81f3ee13b10f

https://www.youtube.com/watch？v=4vGiHC35j9s

編輯：jq