摘 要： 在巖心三維模型中，中軸是描述孔隙結構特征的一種重要表示方法。針對現(xiàn)有的拓撲細化和距離變換方法存在的中軸提取不準確和不連續(xù)的問題，提出了一種使用快速行進水平集方法進行距離變換的三維中軸提取算法。對比實驗結果表明，該算法中提取的中軸在準確性和連續(xù)性上有著較好的保證，實際應用中效果良好。

0 引言

三維模型分析技術在分析巖心孔隙結構和其相應的統(tǒng)計特性中有著重要的應用，中軸骨架是孔隙三維模型分析中的一項重要參數(shù)。中軸骨架表現(xiàn)出了三維模型的拓撲結構，使用中軸描述三維模型不僅能很好地表示三維模型的結構信息，而且還能提高內(nèi)存的使用率和數(shù)據(jù)壓縮率。在巖心三維模型分析中，將中軸應用于模型的迂曲度計算，有著重要的實際意義和工程應用價值。

國內(nèi)外已有許多學者對三維中軸提取進行了研究，目前的三維圖像骨架化方法主要有拓撲細化方法、基于距離變換的方法、基于V圖的方法等。

拓撲細化算法［1-2］能較好地保證拓撲結構，但對邊界噪聲較為敏感，不能保證中軸位置的準確性。距離變換算法［3-5］能夠提取出不規(guī)則物體的骨架并且具有平移、旋轉(zhuǎn)、縮放不變性，但是很難保證模型的連通性。V圖方法［6-7］是利用V圖思想以中軸面或中軸線為基礎得到模型的骨架，一般用于生成多尺度的骨架。此外還有將距離變換和迭代并行細化相結合的方法［8］，得出的骨架具有良好的連通性和拓撲等價性，但對于三維體數(shù)據(jù)需要多次迭代，計算量較大。

本文針對巖心三維孔隙模型進行迂曲度計算等需求，提出了一種使用水平集進行距離變換的方法求解三維結構的骨架，使用水平集的距離變換算法與一般的距離變換方法相比具有更好的穩(wěn)定性和拓撲無關性，解決了距離變換存在的連通性問題。該方法提取出的中軸骨架具有很好的連通性和拓撲等價性。

1 水平集方法

水平集方法是1988年由OSHER S和SETHIAN J首次提出的［9］，用于解決遵循熱力學方程下火苗外形的變化過程。其基本思想是將曲面

（用x表示）看成高一維空間中某一函數(shù)

（稱為水平集函數(shù)）的零水平集，同時曲面的演化也擴充到高一維的空間中。曲線的演化轉(zhuǎn)化成一個純粹的求偏微分方程數(shù)值解問題。在任何時間，波前的位置可以由水平集函數(shù)

的零水平集來確定。將水平集函數(shù)按照它所滿足的發(fā)展方程進行演化或迭代，由于水平集函數(shù)不斷進行演化，所以對應的零水平集也在不斷變化，當水平集演化趨于平穩(wěn)時，演化停止，得到界面形狀。

假設

以速度F沿x（t）法線的方向進行移動，若波前的粒子在路徑上，則粒子的水平集值必定為0：

其全微分方程為：

由于曲線沿法線方向移動，F(xiàn)可以表示為：

結合以上各式可以得出：

這就是參考文獻［9］給出的水平集公式。

2 快速行進方法

考慮波前以速度F沿一個方向運動，根據(jù)速度函數(shù)的符號，波前單調(diào)遞增或遞減傳播，計算每個點的到達時間。運動公式可以表示為：

其中，F(xiàn)是速度函數(shù)，T是到達時間。

在三維空間中，求解上述等式需要計算出每個點（x，y，z）的到達時間。三維空間中梯度的離散化形式為：

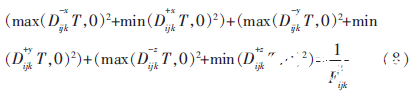
為了求解這個等式，SETHIAN J［10］提出了一種簡單但是低精度的公式：

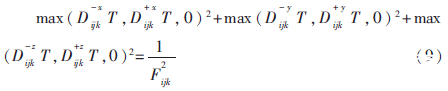
式中前向差分和后向差分的表現(xiàn)形式如下：

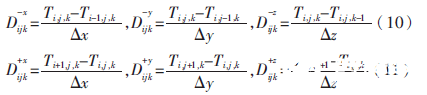
快速行進算法的更新過程如下：

（1）從初始點開始推進算法。將初始點加入到已知點集合，標記為Known。

（2）找出Known點的鄰域，對鄰域點計算到達時間，將求解點標記為trial。

（3）選取trial中到達時間最小的點，標記為Known。

（4）查找所有Known點鄰域內(nèi)所有的未標記點，對其計算到達時間，將求解點標記為trial。

（5）轉(zhuǎn)至步驟（3），直到遍歷所有點，退出循環(huán)，算法結束。

3 使用水平集方法進行距離變換求解骨架

在本文算法中，首先提取出三維模型中所有的連通目標，獨立處理每個連通目標。對每個連通目標進行距離變換，求解距離場D（x，y，z）。距離場是目標中所有體素點到邊界距離的最小值，可以通過計算歐氏距離得到。選取距離場中具有最大距離的體素點作為全局最大距離點。根據(jù)距離場計算速度函數(shù)：

選取全局最大距離點作為目標的中心點，將目標的邊界體素點作為水平集曲線，使用快速行進方法進行演化，演化速度由速度函數(shù)決定。在每個體素更新的過程中，快速行進算法計算出了當前體素點到起點的到達時間。

對于各向同性的快速行進方法，沿著波前的垂直方向波傳播得最快。由于每個中軸點梯度的方向始終垂直于波前，因此中軸體素點具有最快的傳播速度，可以根據(jù)這一特性來提取出中軸體素點，三維模型的中軸即可通過選定的初始體素沿著到達時間的梯度方向回溯求得。

三維模型單個孔隙目標中軸提取流程如下：

（1）求解三維模型的距離場，根據(jù)距離場求解出速度函數(shù)和全局最大距離點。

（2）提取三維模型中所有獨立的連通目標，對每個目標，將全局最大距離點加入點源集合，利用速度圖像，用快速行進方法求解水平集，得到到達時間，將距離點源集合到達時間最大的點作為回溯起始點。

（3）從回溯起始點開始，沿著到達時間的梯度方向開始回溯，一直回溯到點源集合為止。回溯完成后得到一條由最遠點到點源集合的一條分支。

（4）判斷分支長度。若分支長度大于距離場中的最大值，則認為這條分支是中軸的一部分，把分支加入中軸中，并且將該分支中的所有點加入點源集合；若分支長度小于距離場中的最大值，則剔除掉該分支，并且該目標的中軸提取完成。

4 實驗結果分析

本文以下的測試使用圖1所示的巖心三維模型，針對拓撲細化方法和本文提出的基于快速行進水平集方法兩種不同的中軸提取算法進行了對比。兩種方法提取中的中軸結果如圖2所示。

從圖2可以看出，拓撲細化方法保持了中軸的連通性，但是逐步剔除邊界點時，為了保證單像素性，產(chǎn)生了很多折線。使用這種中軸計算三維孔隙圖像的迂曲度時會產(chǎn)生較大的誤差。從圖3可以看出，本文使用的算法提取出的中軸較為平滑，在保持連通性的同時，很好地解決了折線的問題。圖4為本文提取出的中軸和三維模型的疊加顯示，可以看出本文算法提取出的中軸在連通性和正確性上得到了保證。

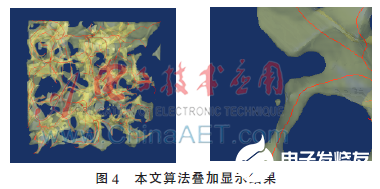
5 結論

本文使用快速行進的水平集方法實現(xiàn)了巖心三維孔隙模型的中軸提取，通過對比實驗，可以看出本文提出的算法有著明顯的優(yōu)勢，提取出的骨架有著很好的準確性和連通性，有實際意義和應用價值。

參考文獻

［1］ 王廣壘，張維忠，宋明玉，等。基于數(shù)學形態(tài)學的鞋楦特征曲線骨架的提取方法［J］。青島大學學報（自然科學版），2012，25（2）：43-46.

［2］ 徐瑩。基于數(shù)學形態(tài)學的圖像骨架提取和復原的改進算法［J］。成都信息工程學院學報，2009，24（3）：259-263.

［3］ 張國棟，韓佳池。基于模糊距離變換的骨架剪枝算法［J］。沈陽航空航天大學學報，2012，29（1）：64-69.

［4］ GAGVANI N， KENCHAMMANA H D， SILVER D. Volume animation using the skeleton tree［C］。 Proceedings of IEEE Volume Visualization， 1998：47-53.

［5］ DEY T K， SUN J. Defining and computing curve-skeletons with medial geodesic function［C］。 Proceedings of the fourth Eurographics Symposium on Geometry processing， AirelaVille， Switzerland， Eurographics Association， 2006： 143-152.

［6］ 劉輝，秦茂玲，徐海峰。基于Reeb圖的三維網(wǎng)格模型骨架提取算法［J］。信息技術與信息化，2012，24（5）：1672-9528.

［7］ 吳艷花。三維模型骨架提取算法及其在檢索中的應用［D］。廣州：中山大學，2013.

［8］ 滕奇志，康瑕，唐棠，等。基于升序復核的并行三維圖像骨架化算法［J］。光學精密工程，2009，17（10）：2528-2534.

［9］ OSHER S， SETHIAN J A. Fronts propagating with curvature-dependent speed： algorithms based on Hamilton-Jacobi formulations［J］。 Journal of Computational Physics， 1988，79：12-49.

［10］ SETHIAN J A. Level sets methods and fast marching methods（2nd edition）［M］.Cambridge University Press，1999.

編輯：jq