二進(jìn)制加法

我已經(jīng)忘了是什么時候?qū)W的加法了，應(yīng)該是小學(xué)吧，先學(xué)10以內(nèi)的，再學(xué)100以內(nèi)的，然后不管多大的數(shù)都可以隨便加了，算式很簡單，就是逢10進(jìn)1。

下面這個式子是一個萬以內(nèi)的加法：

相應(yīng)的，二進(jìn)制就是逢2進(jìn)1，下面這個式子是2個8位二進(jìn)制數(shù)的加法計算：

半加器

8位二進(jìn)制數(shù)還太復(fù)雜，我們先來看看1位二進(jìn)制數(shù)怎么計算的，一共有以下4種情況：

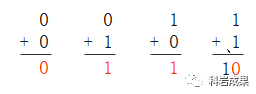
觀察一下就能發(fā)現(xiàn)2個規(guī)律。

第一個規(guī)律，只考慮加法，不考慮進(jìn)位時，加數(shù)與和之間的關(guān)系如下：

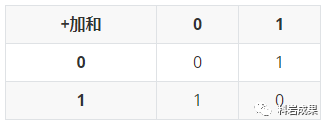
相同為0，不同為1。這個關(guān)系和「異或門」是相同的：

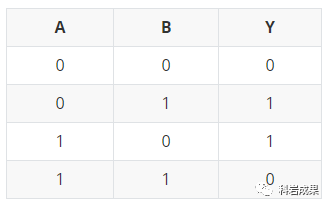
異或門我們之前沒有聊到過，電路圖長這樣：

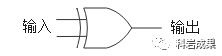
第二個規(guī)律是，如果只考慮進(jìn)位，不考慮加法，加數(shù)與進(jìn)位之間的關(guān)系如下：

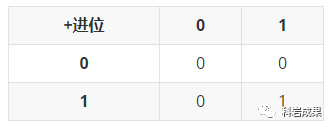
只有全1時，才為1。發(fā)現(xiàn)了嗎，這和本文開頭與門的真值表是一樣的。

2個一位二進(jìn)制數(shù)相加將產(chǎn)生一個加法位和一個進(jìn)位位，加法位輸入與輸出的關(guān)系跟與門是一樣的，進(jìn)位位跟異或門相同。

所以，可以像這樣把兩個門電路連起來，計算2個二進(jìn)制數(shù)（A和B）的和：

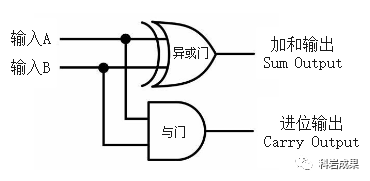
我們稱這個電路為「半加器」，因為它只能計算2個一位二進(jìn)制數(shù)的加法，沒有辦法將前面加法可能產(chǎn)生的進(jìn)位納入下一次計算中，如果有進(jìn)位則實際上是需要3個加數(shù)參與計算。

用門電路畫太復(fù)雜，可以封裝起來這樣表示半加器：

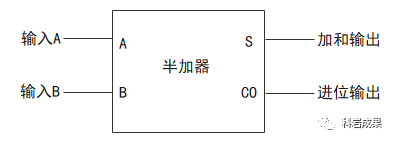
全加器

怎樣計算3個加數(shù)的二進(jìn)制加法呢？需要將2個半加器和一個或門如圖連接起來：

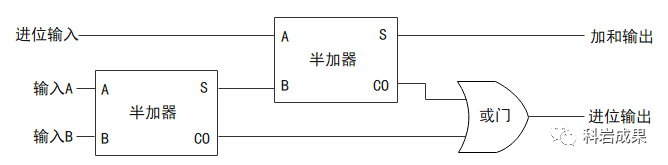
左邊能看到它有3個輸入，右邊依舊是1位加和輸出，1位進(jìn)位輸出。

2個數(shù)的加和與上一次的進(jìn)位相加，得出的加和作為3個數(shù)最終的加和；2個數(shù)相加或3個數(shù)相加的進(jìn)位作為3個數(shù)加和最終的進(jìn)位位。

用文字描述有點不好理解，把這個電路圖全部輸入和輸出情況都展示出來，畫一個表就明白了：

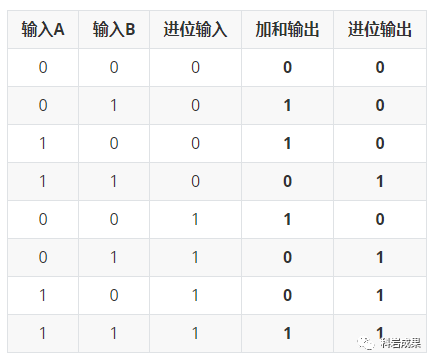
很明顯，這個表就是2個一位二進(jìn)制數(shù)帶進(jìn)位的全部狀態(tài)。

每次做加法時畫2個半加器和一個或門很麻煩，我們用下面這個圖示把它們封裝起來，這個能計算3位二進(jìn)制數(shù)加法的電路就稱為「全加器」。

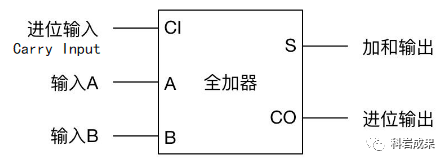
加法器

現(xiàn)在回到開頭那個二進(jìn)制加法：

它有8個二進(jìn)制位，到目前為止我們還只能計算2個一位二進(jìn)制數(shù)，最多再增加一個進(jìn)位的加法，我們最終的目標(biāo)當(dāng)然是2個8位、16位乃至32位數(shù)的加法。

其實，非常簡單，用8個全加器一塊算！

把8個全加器每個進(jìn)位輸出作為下一個的進(jìn)位輸入，首尾相連就可以啦！

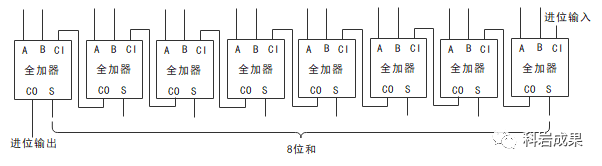
每次這樣畫太麻煩，可以封裝成一個框圖：

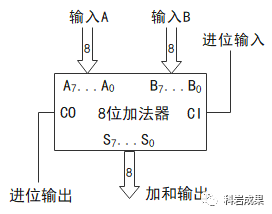
大箭頭代表8個輸入/輸出端，有8個獨立的信號。

一旦我們擁有了8位二進(jìn)制加法器，把它們級聯(lián)起來，很容易就能得到一個16位或32位的加法器啦。

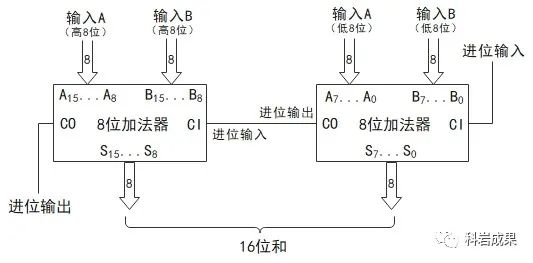
end

加法計算是計算機的基本運算，其實，計算機唯一的工作就是做加法計算。不論是減法、乘法、除法、在線支付、火箭升空還是AI下棋，都是利用加法實現(xiàn)的。

把加減乘除和邏輯運算等運算單元集成起來，就組成了CPU中的基本計算單元：ALU（算術(shù)邏輯單元Arithmetic and Logic Unit）。

用加法器計算2個數(shù)的加法其實就是用硬件方式實現(xiàn)了一個加法計算器，輸入A和輸入B的高低電平?jīng)Q定了輸出S和CO的高低電平。

這樣的電路同一時刻只能表示一種狀態(tài)，只要改變了A、B中任意一位，輸出就會有所變化。

現(xiàn)在我們想計算更多二進(jìn)制數(shù)的加法，比如5個數(shù)A、B、C、D、E的加法（先不考慮進(jìn)位）。

步驟應(yīng)該是這樣：首先把A、B作為輸入，得出一個輸出S1，我們要記下來S1的值，然后把S1和C作為輸入，得出S2....以此類推，要記下很多個數(shù)，然后再用加法器計算。

5個數(shù)都已經(jīng)很麻煩了，如果要計算更多個數(shù)該怎么辦？能不能把每次計算完的結(jié)果存起來，下次繼續(xù)使用呢？

我們的需求

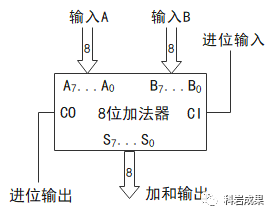
這個加法器有個特點，就是兩個加數(shù)A和B的值決定著加和S的值。

這個值是實時決定的，也就是說，A、B中只要有一個數(shù)據(jù)位發(fā)生了改變（0變1或1變0），加和就一定、立即發(fā)生改變。

我們?nèi)绻胗眠@個加法器算「累加和」將會很麻煩，比如5個數(shù)A、B、C、D、E的加法。

首先把A、B作為輸入，得出一個輸出S1，我們要記下來S1的值，然后把S1和C作為輸入，得出S2....以此類推，要記下很多個數(shù)，然后再用加法器計算。

工程師怎么會做這種無腦循環(huán)的工作呢，得想辦法交給計算機寄幾做。

好像只要做一個什么器件連在這個加法器的輸出上，這個新器件能夠保存加法器輸出的和，并將算好的和再作為一個參數(shù)輸入，傳遞給加法器就可以了。

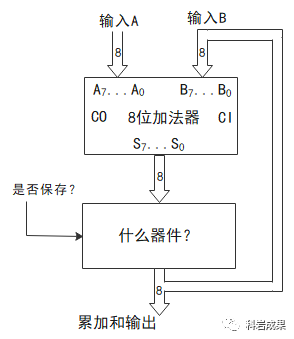
注意這個新器件，首先它支持輸入和輸出；其次它能「保存」當(dāng)前的值；最后，有一個類似「開關(guān)」的引腳決定它是否保持當(dāng)前的值。

「保存」是什么意思？其實很好理解，就是不論輸入的數(shù)據(jù)位怎么變化，輸出都不變。

不考慮8個數(shù)據(jù)位，先只搭建一個這樣具有「保存」功能的門電路，能保存一個bit就ok。

或非門點燈

科巖已經(jīng)點燈無數(shù)，這次依然從點燈開始，用或非門試一下。

「或非門」的真值關(guān)系如下表，記住輸入只要有1，輸出一定為0就可以了。

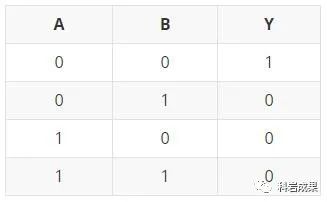
或非門的符號：

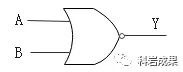
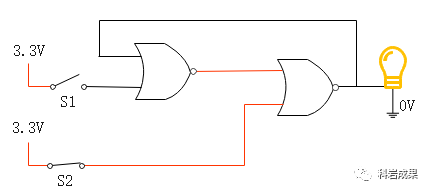
按照下面這個電路把兩個或非門與一個小燈泡連起來，如圖：

仔細(xì)觀察，能發(fā)現(xiàn)我把右邊或非門的輸出直接作為輸入連接到左邊或非門上，這會產(chǎn)生什么神奇的現(xiàn)象呢？

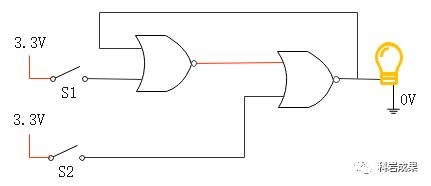
如上圖，最開始，左邊或非門的輸入都是0，輸出為1；右邊或非門輸入一個是0，一個是1，輸出0，燈泡是不亮的。

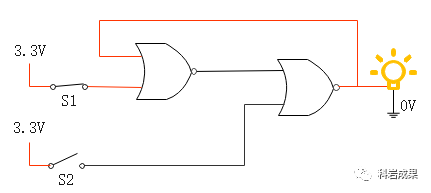
現(xiàn)在把開關(guān)S1連通，連通瞬間，左邊或非門輸出0，右邊或非門輸出1，燈泡被點亮，然后右邊或非門輸出的1給到左邊或非門，2個輸入都是1，它的輸出為0保持不變，燈泡點亮不變。

接著我們把開關(guān)S1斷開，如下圖神奇的事情發(fā)生了，燈泡依然保持點亮狀態(tài)！因為左邊或非門仍有一個輸入是1。

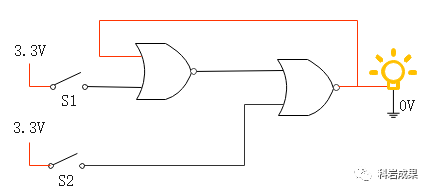
如果把S2閉合會怎樣呢？燈泡馬上熄滅了。

這時再打開S2，電路回到最初的狀態(tài)，燈泡還是熄滅狀態(tài)。

可以總結(jié)規(guī)律了：

?導(dǎo)通S1，燈泡點亮，不論我們怎么控制S1，燈泡都是亮的?導(dǎo)通S2，燈泡熄滅，不論我們怎么控制S2，燈泡都是亮的

這不就達(dá)到我們想要的「保存」功能了嘛，不論輸入的數(shù)據(jù)位怎么變化，輸出都不變。

觸發(fā)器（Flip-Flop）

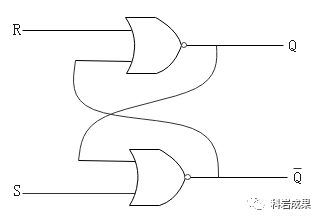
像上面把兩個或非門連起來，能夠穩(wěn)定保存電路狀態(tài)的電路被稱為「觸發(fā)器」。

Flip-Flop的意思是「翻轉(zhuǎn)」，中文翻譯比較奇怪，我們通常理解的觸發(fā)器是Trigger，不過沒關(guān)系，其實就是個名稱而已。

上面這個觸發(fā)器叫做R-S觸發(fā)器，它有2個輸入端S（Set）和R（Reset），2個輸出端Q和~Q（實在打不出Q上面的橫線o(╥﹏╥)o）。

當(dāng)S為1時，輸出Q為1，~Q為0；當(dāng)R為1時，輸出Q為0，~Q為1；當(dāng)S和R都為0時，輸出Q和~Q保持不變；當(dāng)S和R都為1時是一個不正確的狀態(tài)，我們不使用這個狀態(tài)。

不是特別繞吧？畫個表：

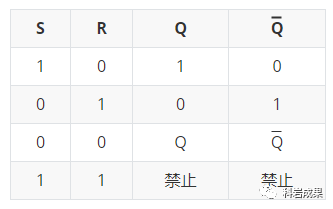
R-S觸發(fā)器最大特點就是它能記住2個輸入端的狀態(tài)。想要記住上一次的狀態(tài)時，把2個輸入端都置0就可以了。

每次畫2個或非門太麻煩，封裝一下：

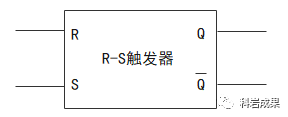
end

有了觸發(fā)器，計算機除了算些加減乘除、與或非邏輯運算，開始具備了存儲功能，我覺得觸發(fā)器真是一個神奇的存在，把平平無奇的門電路連起來竟然就賦予了計算機「記憶」。

計算機中寄存器（Register）、內(nèi)存（RAM）最最基礎(chǔ)的組成單元就是觸發(fā)器。

理解了觸發(fā)器的工作原理，也就理解了內(nèi)存的工作原理。

編輯：jq