拓撲學,英文為 Topology,最初是幾何學的一個分支。通常的幾何學是研究平面或幾何體上點、線、面之間的位置關系以及它們的度量性質;拓撲學對研究對象的長短、大小、面積、體積等度量性質和位置關系都不關心,而是研究幾何形狀在連續形變下的不變性,即“拓撲不變性”和“拓撲等價性”等內容。
在通常的平面幾何和立體幾何中,兩個圖形等價,是要求兩個圖形通過平移、旋轉等操作能夠完全重合;在拓撲學里所研究的圖形,大小、形狀都可以改變,但是表面的點、線的結合關系、順序關系應該保持不變。如圖1,粉色的圖形通過連續的變形可以從球逐漸變成雞蛋、表面凹陷的球、類似鴨舌帽的圖形等。
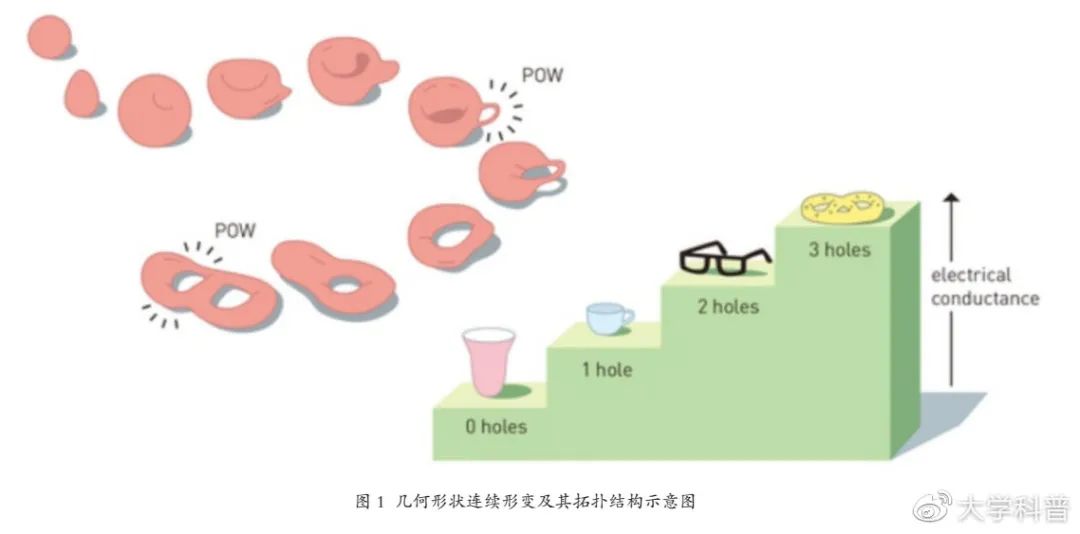
在幾何拓撲的基礎上,通過幾何的微分形式研究體系的整體性質就是微分拓撲,其包含兩個核心概念:底流形和纖維叢。流形是歐幾里德空間的一個子集,這個子集不一定是平直的,可以是一個平面、一個球面等幾何形狀。
底流形,顧名思義就相當于我們選取的一個基底空間。纖維,就是定義在基底空間上的可參數化的空間。例如,向量空間等,而纖維叢就是基底空間與纖維空間的乘積空間。例如,二維平面可以看成是兩個一維平面的乘積,圓柱面可以看作是圓圈和一維直線空間的乘積。纖維叢的一個形象比喻就是一把卷發梳:底流形是梳柄,而纖維則是上面的一根根梳齒。
微分拓撲已在物理研究中發揮重要的作用。例如,高能物理中的規范反常和引力反常,凝聚態物理中的整數量子霍爾效應,分數電荷等,都與各種物理空間中的拓撲性質相關。
拿一個二維體系的電子結構舉例:在二維體系中,考慮周期性邊界條件,其動量空間張成了輪胎面狀的布里淵區(底流形),布里淵區內所有占據態的布洛赫波函數以及布里淵區就構成了纖維叢,可以借助微分幾何的概念來刻畫材料電子結構的拓撲性質。

“拓撲”與磁性的第一次結合是整數量子霍爾效應
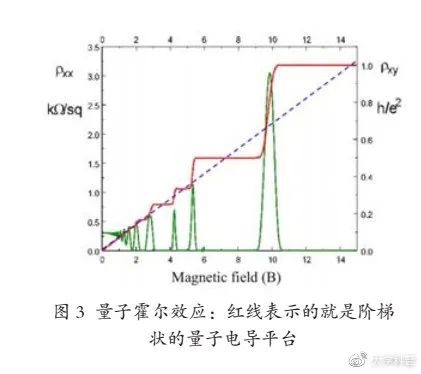
1980年,Von Klitzing等發現二維電子氣在極低溫條件下,隨著外加磁場的增強,霍爾電導不再隨磁場連續變化,而是呈現出一個個量子化的平臺,如圖3所示。因此項研究,Von Klitzing獲得了1985年的諾貝爾物理學獎。
在量子霍爾效應體系中,材料的邊界上會形成一些貫穿能隙的邊界態,邊界態的數目對應于陳數(一種拓撲數)。D.Thouless最早利用微分拓撲中的陳數解釋了量子霍爾電導平臺的穩定性,他也因為這一工作獲得了2016年的諾貝爾物理學獎。
從2005年開始,拓撲學的知識在固體物理中得到了廣泛的應用。Kane和 Mele等在研究二維石墨烯時最早提出了“拓撲絕緣體”的概念。二維拓撲絕緣體,又稱量子自旋霍爾效應絕緣體,是一種全新的量子物態,它的體態是絕緣的,但是在邊界上存在拓撲保護的、能夠導電的邊界態。
如圖4所示,量子自旋霍爾邊界態具有重要的“自旋過濾”特性:在邊界上,自旋向上的電子都向右運動,而自旋向下的電子向左傳播,彼此互不干擾,可以有效抑制“背散射”。因此,量子自旋霍爾效應體系在微納尺度是無電阻的理想導體。
“拓撲”與磁性的第二次結合是量子反常霍爾效應的實現
量子反常霍爾效應不同于量子霍爾效應,它的產生不依賴于外加磁場而由材料本身的磁化產生。早在1988年,Haldane就提出了一種在六角晶格中實現這種無外加磁場的量子霍爾效應的理論模型,由此他也分享了2016年的諾貝爾物理學獎。
2013年,薛其坤院士團隊在實驗上首次觀測到了量子反常霍爾效應,該工作獲得了國家自然科學一等獎,其本人也獲得了2020年度的菲列茲·倫敦獎,成為首個獲得這一榮譽的中國科學家。
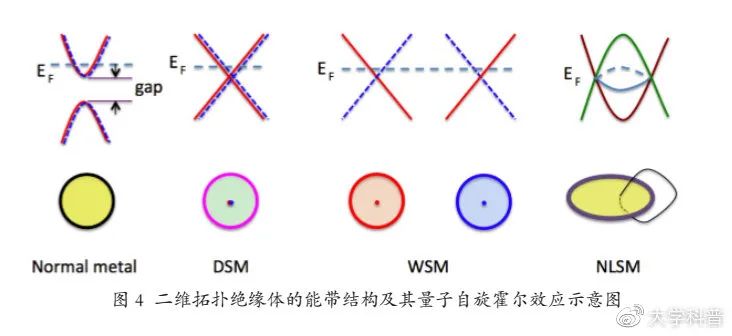
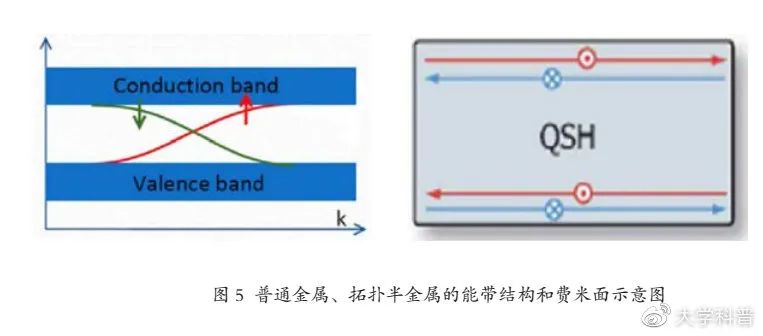
2011年,隨著對拓撲絕緣體的深入研究,人們又發現了拓撲半金屬:它的能隙為零,費米面是孤立的點或者閉合的線。拓撲半金屬是不同于拓撲絕緣體的一類新的拓撲量子態。根據節點的簡并狀況及在動量空間中的分布,拓撲半金屬可以細分為外爾半金屬(WSM)、狄拉克半金屬(DSM)和節點線半金屬(NLSM)等。
如圖5所示,前兩種半金屬的費米面是動量空間中幾個孤立的費米點,而NLSM中的費米面是一維的閉合環線。與拓撲絕緣體一樣,拓撲半金屬也有許多新奇的物性,包括動量空間中的磁單極子、費米弧、外爾異常和負磁阻效應等。
“拓撲”與磁性的第三次結合是磁性拓撲半金屬
2011年,萬賢剛等最早預言了燒綠石結構的反鐵磁處于一種外爾半金屬相。隨后,徐剛等發現了尖晶石結構中鐵磁態的三維拓撲半金屬 HgCr2Se4。自此,越來越多的磁性Weyl半金屬材料相繼提出,包括Heusler化合物、Kagome層狀材料和蜂窩狀晶格材料等。
與此同時,對于磁性Dirac半金屬材料的研究也獲得廣泛關注,包括CuMnAs、EuCd2As2等材料體系被相繼提出。磁性NLSM體系包括層狀的Fe3GeTe2和LaCl等。
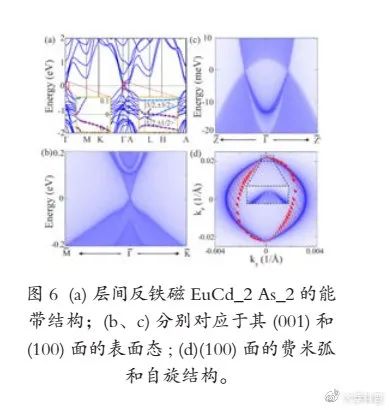
這里我們選取EuCd2As2體系作為磁性拓撲半金屬的例子,簡單介紹其新穎的拓撲物性。EuCd2As2是一種具有層間反鐵磁結構的狄拉克半金屬,在費米能級上只存在一對狄拉克點,如圖6所示。
通過調整磁矩方向,在EuCd2As2中還可以實現軸子絕緣體等新奇拓撲物態——在其某些表面上可以打開表面態的能隙,實現半整數量子霍爾效應、拓撲磁電效應、軸子極化激元等物理現象。EuCd2As2的發現為研究拓撲相變和新型反鐵磁拓撲物態提供了一個理想平臺。
相比于非磁拓撲材料,磁性拓撲材料最大的優勢就是通過外加磁場可以有效調控磁性拓撲材料的磁化方向,從而實現不同拓撲態之間的拓撲相變。例如,外加磁場可以實現磁性拓撲半金屬到“量子反常霍爾態”、軸子絕緣體的轉變。
這些拓撲轉變可以巨大地改變材料的物理性質,可以用來設計拓撲電子學器件。除了電學、磁學方面的新奇物性,磁性拓撲材料在光學等其他領域也有應用,包括實現拓撲磁光效應、用于宇宙暗物質探測等。
與拓撲相關的研究還包括高階拓撲絕緣體、非厄米系統中的拓撲態、磁性-超導材料異質結中的拓撲超導態等。這些前沿研究具有廣泛而深遠的戰略意義。其中,拓撲與磁性的結合尤為重要。一方面它可以提升我國的科研創新能力,另一方面相關量子現象的探測和調控研究將為新一代自旋電子器件、量子通信、拓撲量子計算機等領域打下堅實的理論基礎和材料基礎。
編輯:jq
-
拓撲
+關注
關注
4文章
341瀏覽量
29590 -
電子學
+關注
關注
4文章
61瀏覽量
12803 -
絕緣體
+關注
關注
1文章
47瀏覽量
4751
原文標題:“拓撲”與磁性的結合
文章出處:【微信號:cas-ciomp,微信公眾號:中科院長春光機所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
鐵磁性的概念、產生機理、應用
產業"內卷化"下磁性元件面臨的機遇與挑戰

如何利用磁場相機實現先進的磁性微結構分析?

磁性元器件.pdf
什么是順磁性材料
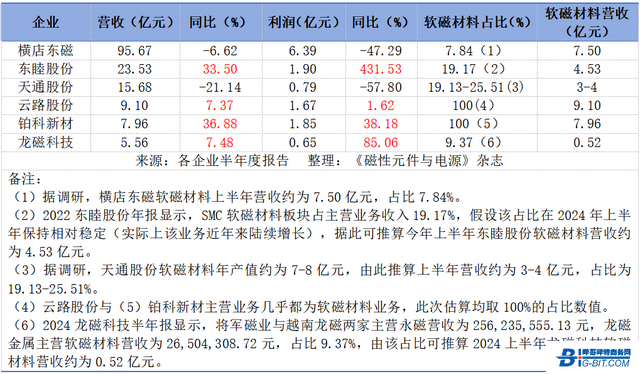
磁性材料企業半年報亮點紛呈,關注這些領域
半橋llc諧振拓撲優點缺點是什么
磁性開關可以由什么構成
什么是磁性開關?磁性開關是如何接線的
LLC諧振變換器拓撲構成與工作原理分析





 剖析拓撲與磁性的結合
剖析拓撲與磁性的結合










評論