沒有，科普結束。

然而，初中學過卡文迪許扭秤實驗的你一定不甘心就這么結束。既然物理中有這么一個方法叫做二次放大法，那么用同樣或類似的方法是否可以去測量微觀世界的尺度呢？

這個可以有。本篇科普所要實現(xiàn)的，就是盡力用一種較通俗的語言介紹一種測量分子橫截面積的方法：表面張力法。

表面張力是什么？

啊這，要從這里開始解釋嗎？

其實，表面張力的現(xiàn)象你已經見過不下千百回了：下雨時窗玻璃上的雨滴、清晨時綠葉上的露珠、洗衣服產生的大肥皂泡；而在高中你也已經或將要接觸到表面張力的知識。從微觀角度上講，液體的內部是由很多很多分子構成的，這些分子因為相距既沒有氣體分子間那么遠、又不如固體分子間那么近，所以表現(xiàn)出一種可以自由移動但又互相吸引的狀態(tài)。如果用圓圈來表示分子，一杯液面接觸氣體的液體，其微觀狀態(tài)大致如下圖所示。

可能已有讀者注意到，在靠近液面的部分，我所繪制的圓圈——也就是分子，較稀疏。這是因為在氣液分界面處考慮分子熱運動，液體分子會逸散到空氣中，同時空氣中的分子也會進入液體；但是，在等體積情況下，液體的分子更多，因此逸散進入空氣的分子也就更多，所以進入空氣的分子數(shù) > 進入液體的分子數(shù)，進而導致液體表面分子稀疏。

在這種情況下，為了保證液面的連續(xù)性，在體積不變的情況下，我們要用最少的表面分子構筑表面。顯然只有球面滿足這一條件，而有關于等體積時球體表面積最小問題的證明，在這里不再贅述。也就是說，液體表面分子間存在一種力，使得忽略重力作用時液體表面呈球面。維持這種狀態(tài)的力便被稱之為表面張力。

用箭頭代表分子間作用力，顯然液體分子“人數(shù)”更多，優(yōu)勢更大；氣體分子就比較拉了，產生不了多少引力。這個引力差就是表面張力的產生原因（但不是表面張力本身），它讓液面分子有向液體內部下降的趨勢，從而保持表面緊繃。當然，這是一個比較容易通俗解釋的模型，并不是真實現(xiàn)象，實際情況要比這復雜得多。

就比如，表面張力實際上的方向是與液面相切的，那么引力差如何產生這個方向的力呢？要理解的話只能這樣強行解釋：引力差把表面分子向下拉，同時這個分子兩側的表面分子又拉著它不愿意讓它離開，如下圖。

由于這個θ角特別小，分子級別的能有多大呢？咱就直接忽略掉了，這個拉力就是表面張力，與液面相切。

上面說了這么多，都是建立在只有一種液體的前提下。如果我們往這個液體里——就以水為例，加入溶質會怎么樣呢？

那一夜，我不再純潔——

哈哈，指水不再純凈，被加了溶質。別想歪了，晚上做的實驗罷了。

當溶質加入之后，水的表面張力降低，那么根據能量最低原理，表面張力能肯定越小越好，那么水表面的溶質濃度就會比水內部的溶質濃度高一些；反之，則就小一些。這種表面濃度和內部濃度不同的現(xiàn)象被稱作表面吸附。既然有現(xiàn)象，就會有閑著無聊（劃掉）的科學家去尋找現(xiàn)象的規(guī)律，就比如希什科夫斯基這個人：我百度都百度不到這個人的信息，他居然還靠自己的實驗數(shù)據得到了下述經驗公式：

σ＝σ?-σ?αln（1+c/β）

其中σ是溶液表面張力，σ?是溶劑表面張力，都是神秘的系數(shù)，顯然c是溶液濃度。

這個經驗公式是否正確呢？1916年物理化學家朗格繆爾也閑著沒事提出了一個猜想，那就是固體表面的原子或分子存在向外的剩余價力，它可以捕捉氣體分子。這種剩余價力的作用范圍與分子直徑相當，因此吸附劑表面只能發(fā)生單分子層吸附，并給出了朗格繆爾單分子層吸附等溫式，該式在氣液界面的應用形式如下：

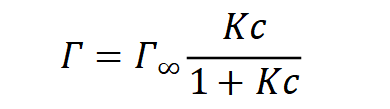
其中Γ是吸附量，Γ∞是極限吸附量，也就是表面全都是吸附分子時的吸附量，可近似看作極限吸附時溶質的物質的量。此時認為液體表面也只能發(fā)生單分子層吸附。如果我們能得到Γ∞，也就意味著分子橫截面積為

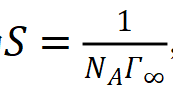
，就回歸初心了。

根據化學熱力學，我們可以推導（過程比較復雜，不再展示）出吉布斯吸附方程：

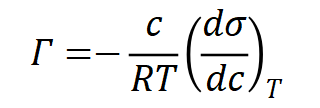
將朗格繆爾公式代入，得到：

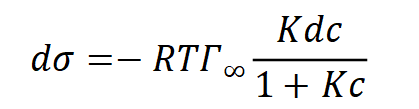
積分得到：

σ＝σ?-RTΓ∞ln（1+kc）

與希什科夫斯基經驗公式形式相同，一是可以證明其正確性，二是為我們最初的主題：測量分子橫截面積找到了出口。只要能夠測出表面張力和溶液濃度，并作出一條曲線，通過模擬這條曲線的函數(shù)關系式，即可得到Γ∞，進而測出分子橫截面積。

溶液濃度可以通過光度計等一系列方法準確測定；表面張力則可以通過在毛細管中形成一個小氣泡，用儀器測定毛細管內外壓力差得到氣泡的附加壓力，當氣泡最小時和毛細管內徑相同，而毛細管內徑數(shù)值可以通過先測量已知表面張力數(shù)值的液體的最大附加壓力得到，此時由拉普拉斯公式可知附加壓力最大并求出表面張力數(shù)值。有關拉普拉斯公式的推導和本文主要內容無關。

實戰(zhàn)！得到正丁醇分子橫截面積！

其實就是因為我實驗做的是正丁醇所以實戰(zhàn)也是這個，有設備的可以自己利用科普的原理，測測其他物質的分子橫截面積。

接下來的內容就是些數(shù)據處理，不算科普范疇。感興趣的可以看看，順便給你們證實一下這種方法的可靠性還是比較高的。

Code:

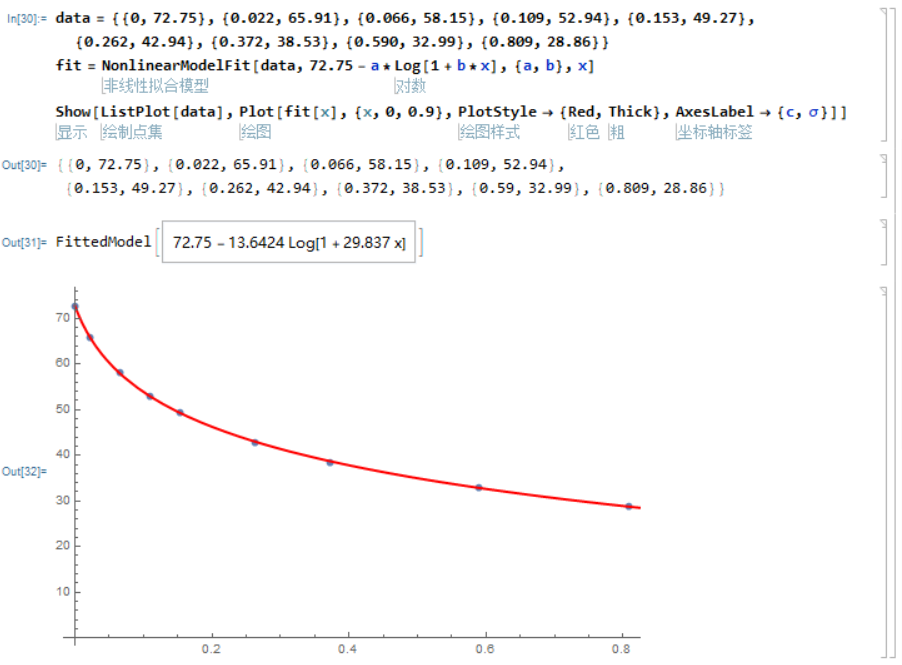
data = {{0, 72.75}, {0.022, 65.91}, {0.066, 58.15}, {0.109,52.94}, {0.153, 49.27}, {0.262, 42.94}, {0.372, 38.53}, {0.590, 32.99}, {0.809, 28.86}}

fit = NonlinearModelFit[data, 72.75 - a*Log[1 + b*x], {a, b}, x]

Show[ListPlot[data], Plot[fit[x], {x, 0, 0.9}, PlotStyle -> {Red, Thick},AxesLabel -> {c, [Sigma]}]]

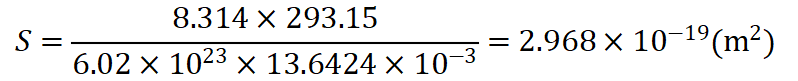
正丁醇分子橫截面積在

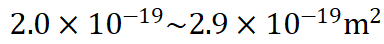
之間，誤差較小。

編輯：jq