天氣越來越熱了，這個時候能舒舒服服沖個澡自然是再開心不過了。但是很多朋友都有過這樣的經(jīng)歷：水龍頭出來的水要么太涼要么太熱，怎么也調(diào)不到滿意的溫度。要解決這個問題，就要涉及到我們今天要說的延遲方程了。

相信大家都有過這樣的經(jīng)歷：在淋浴時感覺水太冷了，所以你打開了熱水龍頭。但是水溫不會馬上變化——因為熱水需要時間來流經(jīng)管道——因此你最終會把溫度調(diào)得更高。之后熱水流過了管道，從花灑流到你身上。但是這時溫度又太高了。于是你馬上把熱水龍頭關(guān)上，但等到效果顯現(xiàn)的時候，水又太冷了。所以你又得把溫度調(diào)高。如此循環(huán)往復(fù)——似乎不可能調(diào)到正確的溫度。

有一個方程可以描述這種情況。從氣候變化到COVID-19，這個等式的應(yīng)用已經(jīng)遠(yuǎn)遠(yuǎn)超出了浴室的范圍。這是因為世界上的很多過程會涉及經(jīng)過延遲才會產(chǎn)生的效應(yīng)。但在講述它的應(yīng)用之前，讓我們看一下這個方程。

方程

The equation

我們寫下在t時刻感受到的水的溫度T(t)。假設(shè)水要花d秒的時間才能流過管道。那么淋浴方程便是

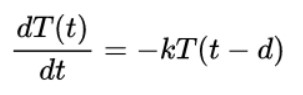
（1）

我們回顧下這個表達(dá)式。左邊表示t時刻水的溫度變化率，正值代表著t時刻水溫增加，負(fù)值代表著t時刻水溫降低。正值越大(或負(fù)值越小),在t時刻的溫度升高(或降低)的速度越快。

方程的右邊告訴我們：t時刻的變化率正比于t時刻之前d秒時的溫度，也就是說，它正比于T(t-d)。這是有道理的：溫度在t時刻的變化率取決于你在(t-d)時刻提高(或降低)多少熱量，而這顯然取決于你當(dāng)時感覺水有多熱或多冷。數(shù)字k是比例常數(shù)(我們假設(shè)它大于0)。

最后，這個負(fù)號反映了這樣一個事實：(t-d)時刻的高溫意味著你會調(diào)低溫度，從而導(dǎo)致t時刻的溫度降低；而(t-d)時刻的低溫意味著你會調(diào)高溫度，從而導(dǎo)致t時刻的溫度升高。

好吧，這有一點不準(zhǔn)確的地方：嚴(yán)格來說，這個方程告訴我們：如果溫度低于0，你就會提高溫度，如果溫度高于0，你就會降低溫度。這顯然不太準(zhǔn)確，因為僅僅高于0是遠(yuǎn)遠(yuǎn)不夠溫暖的。然而，我們可以很容易調(diào)整這個方程使得它反映這樣一個事實：你可以用某個理想值（除0℃外)為參考點來調(diào)高或調(diào)低溫度。

求解這個方程意味著找到滿足它的函數(shù)T(t)。這個函數(shù)T(t)會給出任意t時刻的溫度。充分了解這個函數(shù)后，你就會知道，開關(guān)熱水龍頭究竟是會保持一個舒適的溫度，還是會讓你一直開下去而得不到一個滿意的結(jié)果。

由于我們的方程涉及到變化率，也被稱為導(dǎo)數(shù)，所以這個方程被稱為微分方程。這樣的方程很少有容易求解的，但我們至少可以探索它的解是什么形式。這需要一點微積分知識。如果你還沒有準(zhǔn)備好，你可能想要跳到這篇文章的最后一部分，在那里我們將認(rèn)識到淋浴方程的重要應(yīng)用。

不含延遲

讓我們先看看如果水穿過管道完全不需要時間會發(fā)生什么——這樣就沒有延遲：d=0。方程(1)變成

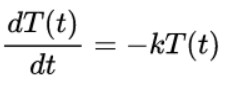
如果你知道一點微分你就會知道下面這個函數(shù)

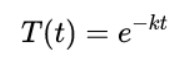
是這種情況的一個解。下面是這個函數(shù)的不同值的圖。在任意一種情況下，我們看到溫度的行為都是穩(wěn)定的：它收斂到0值（前面提到，我們假設(shè)這是我們追求的理想溫度）。

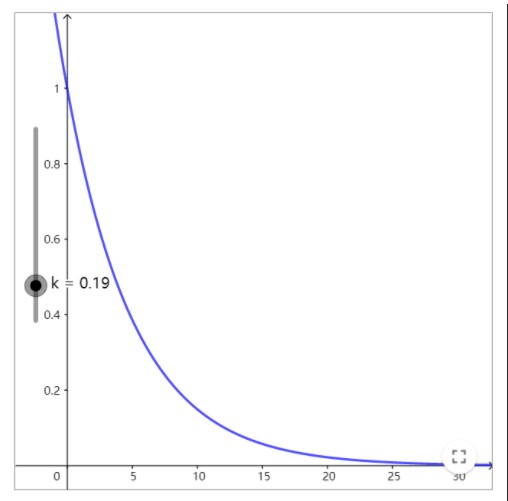
kd=0.19時的圖像（點擊圖片可以改變參數(shù)得到更多圖像）

存在延遲

當(dāng)有延遲時，d就不等于0，這時候數(shù)學(xué)就變得困難了——你可以直接跳到文章的結(jié)尾，看看這個方程的應(yīng)用。

假設(shè)解的形式是這樣的

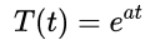? ? ? ? ? （2）

a是一個參數(shù)。我們的任務(wù)是找出參數(shù)a應(yīng)該是怎樣的。方程(2)對t求導(dǎo)得到

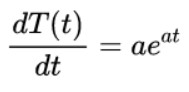
代入原方程(1)得到

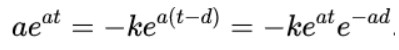
當(dāng)參數(shù)a滿足下面的超越方程時，此方程恰好成立。

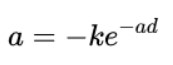? ? ? ? ? （3）

我們可以把它寫成更整潔的形式：

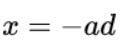
那么方程(3)變成

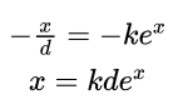
這樣

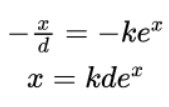
超越方程很難解，但我們能做的就是畫出這兩個函數(shù)，看看它們交點的情況。這些交點的橫坐標(biāo)x滿足式(3)。如下所示（你可以點擊圖片進去使用滑塊來改變(dk)的值）：

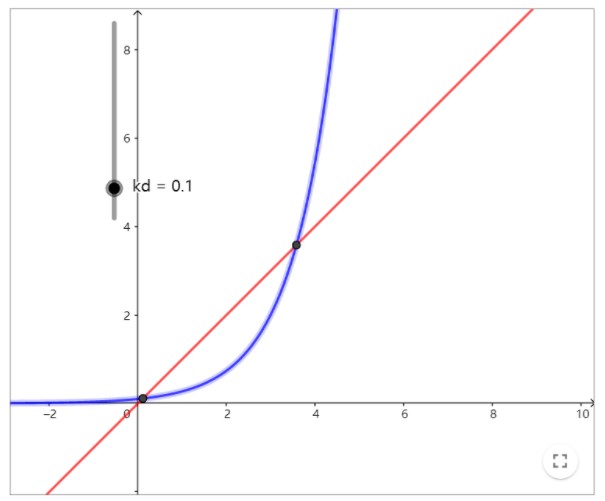
kd=0.1時的圖像（點擊圖片可以改變參數(shù)得到更多圖像）

從圖中可以看出，方程(3)只有當(dāng)時小于0.37左右的某個值時才有解。事實上，它只有當(dāng)

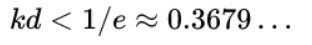
才成立。這里e是自然對數(shù)的底。

這種情況下的解x是正數(shù)。因為x=-ad和d也是正的（記住它表示延遲），這意味著a=-x/d是一個負(fù)數(shù)。

這樣原始的淋浴方程(1)的解具有類似與無延遲的情況下方程解的形式：隨著時間的推移，它將趨于0。換句話說，如果我們的延遲參數(shù)d和比例常數(shù)k的乘積小于或等于1/e，我們開關(guān)熱水龍頭最終會得到一個理想的溫度。

如果kd>1/e將會發(fā)生什么呢？這時我們需要進入復(fù)數(shù)領(lǐng)域：這種情況下，方程(3)沒有實數(shù)解，但它卻有復(fù)數(shù)解。這里我們不詳細(xì)討論，但事實證明，如果這些復(fù)數(shù)解的實部小于0，淋浴的情況仍然是可控的：開關(guān)熱水龍頭最終會讓我們達(dá)到所需的溫度。

然而，如果復(fù)數(shù)解的實部大于0，那么淋浴就不可控制：溫度將持續(xù)上升和下降——當(dāng)然這就讓我們很不爽。根據(jù)延遲參數(shù)d和比例常數(shù)k，這兩種情況之間的轉(zhuǎn)變發(fā)生在乘積(kd)等于π/2的時候。

氣候變化與COVID-19

Climate change and COVID-19

如果你跳過了數(shù)學(xué)部分，現(xiàn)在歡迎來到應(yīng)用部分！我們在數(shù)學(xué)部分得到的結(jié)論是：

如果延遲參數(shù)和比例常數(shù)的乘積(kd)小于π/2，那么淋浴的情況是可控的:開關(guān)熱水龍頭最終會得到我們想要的溫度。

當(dāng)kd<1/e時，這一調(diào)節(jié)過程中溫度不會有任何振蕩；當(dāng)1/e

下面的兩個圖說明了這一點。

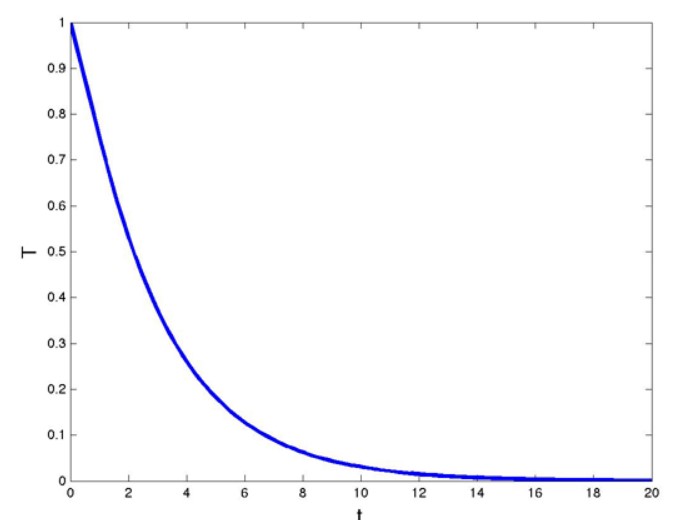
kd=0.25<1/e情況下的溫度函數(shù)

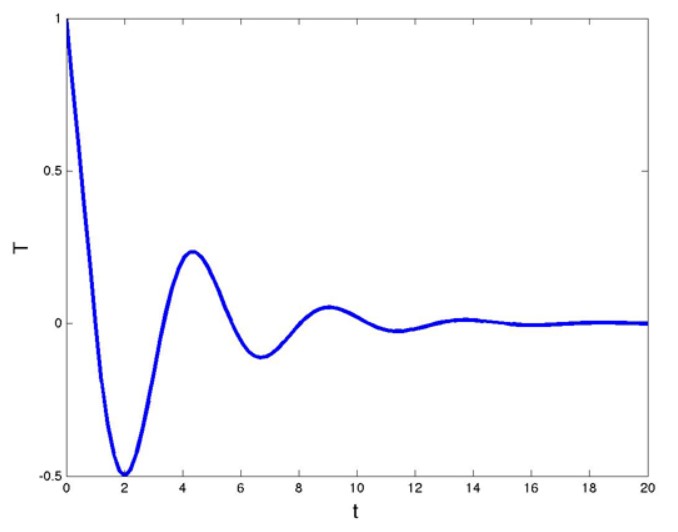
1/e

然而，如果kd>π/2，溫度函數(shù)將繼續(xù)劇烈振蕩，如下圖所示。

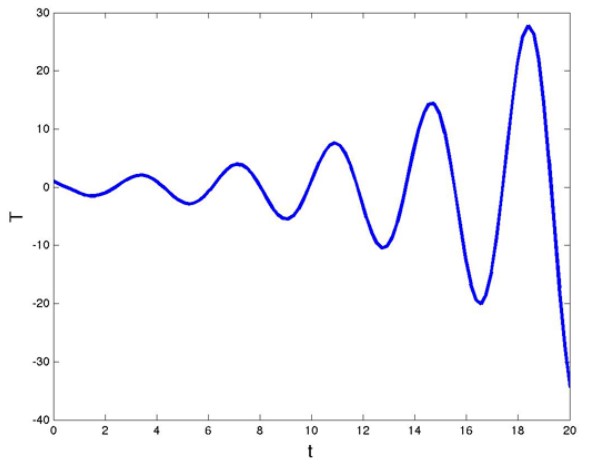
kd=2>π/2情況下的溫度函數(shù)

現(xiàn)在，如前所述，讓我們看看淋浴方程的其他應(yīng)用。最重要的應(yīng)用是對氣候動力學(xué)的研究，因為許多氣候現(xiàn)象需要時間才能產(chǎn)生影響。

例如，如果我們改變現(xiàn)在排放到大氣中的二氧化碳量，那么我們需要等待一段時間，才能看到這對地球溫度的實際影響。這使得很難確定二氧化碳減少的影響，并可能導(dǎo)致不受控制的振蕩。

另一個例子是厄爾尼諾-南方濤動(El Ni?o Southern Oscillation，ENSO)。這是一種熱帶地區(qū)太平洋溫度的不規(guī)則變化，升溫事件周期大約為4年。厄爾尼諾現(xiàn)象不僅影響它出現(xiàn)的地區(qū)，而且對全球經(jīng)濟都有重大影響。如果我們能更好地預(yù)測它，那么這將有助于太平洋地區(qū)的國家和地區(qū)做好準(zhǔn)備。

ENSO是由洋流和大氣之間的相互作用引起的，它改變了海洋的溫度。ENSO可以用一個和淋浴方程非常相像的方程來模擬。在這種情況下，延遲是洋流從南美洲西海岸到亞洲東海岸往返所需要的時間（見上圖）。這導(dǎo)致了我們看到的周期性。事實上在這種情況下，方程包含額外的非線性項，這會導(dǎo)致混沌動力學(xué)疊加在周期振蕩上。

我們的方程同樣適用于理解農(nóng)業(yè)對氣候變化的反應(yīng)。這也涉及到延遲，因為作物需要時間生長，這導(dǎo)致很難在變化的環(huán)境中規(guī)劃何時種植和收獲作物。

淋浴公式也與我們目前因COVID-19而出現(xiàn)的情形非常相關(guān)。回顧我們的眾多舉措，我們通過社交距離和接種疫苗實現(xiàn)了對疫情的有效控制，生產(chǎn)生活已經(jīng)基本恢復(fù)正常。但事實上這些措施需要一段時間才能生效，所以我們要再次處理延遲的問題。此外，COVID-19的病毒潛伏期為5天至2周。在這段潛伏期內(nèi)，沒有明顯的癥狀，所以從一個人被感染到明顯生病之間有一段時間，這在模擬疫情時需要考慮。這直接導(dǎo)致了淋浴方程的不同版本，也就是所謂的包含了延遲和控制的SIR方程，可以用來幫助我們理解和控制流行病。就像ENSO系統(tǒng)一樣，一旦方程中加入了延遲，事情就變得更加不確定。因此，(衛(wèi)生和經(jīng)濟)系統(tǒng)的可控制性如何還有待觀察。

責(zé)任編輯：lq6