900-MHz 和 2.4-GHz 頻段短距離無線設備的設計人員需要了解，公式中的參數對傳輸距離的影響以及這些參數如何影響傳輸距離，同時還要能將這些參數應用到公式中，用于統計計算出室內和戶外環境下的路徑損耗及傳輸距離。

隨著家庭、建筑及工業自動化應用中無線技術的應用，短距離無線設備正倍受關注。通常，這些應用使用專用頻段或以標準協議為基礎的頻段，例如：900-MHz 和 2.4-GHz 的 ISM（工業/科學/醫學）頻段 ZigBee。隨著短距離無線設備應用的不斷普及，對于終端設備設計人員來說，充分了解無線通信距離比以往變得更為重要。這篇文章討論了無線傳播，并開發了一些模型，用來估算室內環境下短距離無線設備的路徑損耗和距離。這些模型讓系統設計人員可以對無線通信系統的性能進行一個初步的估算。

在探討距離估算公式之前，設計人員需要了解無線信道及傳播環境。無線通信信道為發送器和目標接收機之間的傳輸通道。不同于固定的且可預知的有線信道，無線信道具有隨機性和時變性，以及建模的困難性的特點。因此，設計人員需要對這些隨機信道進行統計建模。

無線電波傳播模型的重點一般是在給定發送器距離的路徑下預測出接收信號的平均強度，以及接近一個方位點上的信號強度的變化。對任意發送器－接收機間的平均信號強度進行預測的傳播模型為大型傳播模型，其在估算發送器距離方面極為有用。相反地，在一些波長內接收信號強度的傳播模型為小型模型，或為衰減模型，其具有快速波動的特點。這篇文章重點討論大型傳播模型，該模型可對無線傳輸的距離進行估算。

當發送器和接收機之間具有一條暢通無阻的可視路徑時，自由空間傳播模型可對接收信號的強度進行預測。自由空間傳播模型會做出這樣的預測，接收信號強度“衰減”為發送器－接收機間隔距離的函數，強度衰減升至 N 次冪——“冪律函數”。接收機天線所接收到的自由空間功率與發射天線隔開一段距離，Friis 自由空間方程式把此段距離定義為：

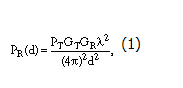
在這個方程式中，PT為發送器功率；PR（d） 為接收功率，并為發射－接收間隔距離 d 的一個函數；GT為發送器天線增益；GR為接收機天線增益；d 為發送器和接收機之間的間隔距離，單位為米；λ 為波長，單位為米。

Friis 自由空間方程式說明了隨著發送器至接收機間隔距離平方值的增加，接收功率不斷下降。這一結果表明接收功率隨著距離的增加將以 20 dB/decade 的速率衰減。

在對無線傳輸距離進行估算時重要的一項是路徑損耗，路徑損耗以 dB 為單位，表示信號衰減程度。路徑損耗為以 dB 為單位計量的發送器天線功率與接收機天線功率之間的差分。通過方程式 1，您可以推算出路徑損耗為發送功率除以接收機功率。方程式 2 將路徑損耗定義為：

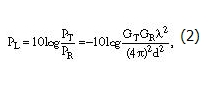
在這個方程式中，PL為路徑損耗。對方程式 2 進行簡化，假設發射天線和接收天線具有相同的增益，那么這一假設得出的結果為：

只有當 d 的值處于發射天線遠場 （far field） 內，Friis 自由空間公式才能對接收功率電平做出估算。發射天線的遠場，即Fraunhofer 區，指的是超出遠場距離 dF的區域。對于一個天線來說，dF為 2D2/λ，其中 D 為天線的最長物理線性尺寸。另外，dF必須大于 D，并且必須處于遠場內。這一路徑損耗公式僅適用于可視路徑暢通無阻的理想化系統，并且您應該只是利用這一公式進行初步估算。

傳播模型將近場 （close-in） 距離d0作為接收功率的參考點。在任何大于與 PR（d0） 相關的接收功率參考點的距離的情況下，您必須計算出接收功率PR（d），PR（d0） 的值可以通過方程式 1 和方程式 4 計算得出。作為一種選擇，您可以通過鄰近發送器的許多點上求取平均接收功率，測算出無線通信環境下的值。您必須選擇一個近距參考距離，從而使遠場區大于近場距離。

通過了解這些知識，您可以使用如下的公式計算出任何距離的接收功率：

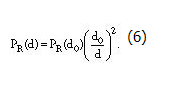
在 1 至 2 GHz 之間運行的應用系統其參考距離為室內環境下 1 米，室外環境下 100 米。

大部分射頻功率電平單位為毫瓦分貝，或者為瓦分貝，而不僅僅是絕對功率電平。您可以將方程式 6 重新整理為：

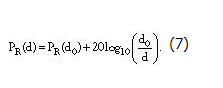
下面的示例闡明了這些概念。 假設發射頻率為 900 MHz，發射功率為 6.3 mW （8 dBm），且發射和接收天線具有相同的增益，則可以測算出室外可視環境下 1200 米處的接收功率。室外環境下，參考距離為 100 米，同時您必須測定出 100 米處的接收功率。波長為 900 MHz 時是 0.33 米。

使用方程式 1 中的值，您將得出：

因此，在一個理想的且暢通無阻的室外可視環境下，當發射功率為 8 dBm 時 1200 米處的接收功率大約為 -85 dBm。由于現實環境下將很可能在可視路徑上存在障礙，或者更糟糕的是根本就不存在可視路徑，所以實際接收功率要低得多。在前一個示例中，您計算出的路徑損耗為 PT–PR。所以，路徑損耗應為 93 dB（8 dBm 減去–85 dBm）。

實際路徑損耗公式

對于任何一個實用的無線傳感器系統而言，了解最大的實際數據傳輸距離都是非常重要的。該無線系統距離直接取決于鏈路預算參數。

LB=PT+GT+GR–RS， （13）

在這一方程式中，LB 為鏈路預算，單位為分貝；PT為發射功率，單位為分貝毫瓦或分貝瓦；GT為發射天線增益，單位為分貝；GR為接收機天線增益，單位為分貝；RS 為接收機靈敏度。靈敏度是指在可接受的 SNR（信噪比）情況下，系統能探測到的最小的 RF 信號。方程式 14 顯示了接收機的靈敏度：

S=–174 dBm/Hz+NF+10logB+SNRMIN， （14）

在這一方程式中，–174 dBm/Hz 為熱噪聲底限，NF 為全部接收機噪聲，單位為分貝，B 為接收機整體帶寬，而 SNRMIN 則為最小信噪比。如果發送器與目標接收機之間的總路徑損耗大于鏈路預算，那么接著就會發生數據丟失，然后無法實現通信。因此，對于研發終端系統的設計人員來說，精確地描述路徑損耗并將路徑損耗與鏈路預算相比較以得出對距離的初步估算，這一點是非常重要的。

室內信道的路徑損耗

室內無線通信信道不同于室外信道，這是由于室內信道具有覆蓋距離較短、更高的路徑損耗變化，以及由此導致的接收信號功率更大的變化特性。但是，對于固定的無線設備來說，接收信號功率的變化性可以忽略不計。建筑物布局、類型及建筑材料都會嚴重影響室內傳播。研究人員將室內信道分類為可視信道，或帶有動態雜波 （clutter） 的受阻信道（見參考書目1）。建筑物的內部及外部結構都有大量的隔離物和障礙物。隔離物的判斷取決于該結構為家居環境還是辦公環境。建筑結構內的隔離物為硬隔離，而可移動且不超過天花板的隔離物為軟隔離。住宅一般使用木制框架隔離物，而辦公建筑通常使用的是軟隔離物，在樓層之間為鋼筋混凝土。

隔離物的物理及電氣特性大相徑庭，這就使得在室內信道使用一般模型變得非常困難。不過，通過大量的研究，已將通用材料類型的信號損失制定成了表格（見表 1）。樓層衰減因素表示樓層之間的隔離物損耗（見表 2）。方程式 15 表示的是在使用對數距離路徑損耗模型下室內信道的實際路徑損耗模型：

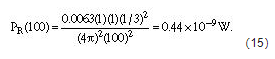
在這一方程式中，X 為一個零平均值正態分布隨機變量，單位為分貝，σ 為標準偏差。如果設備為固定的，您可以忽略 Xσ影響。使用方程式 4 計算出 1 米距離處路徑損耗的值，并將這個值代入方程式 15，將得出：

PL（d）=20log10（fMHz）+10nlog10（d）–28+Xσ。 （16）

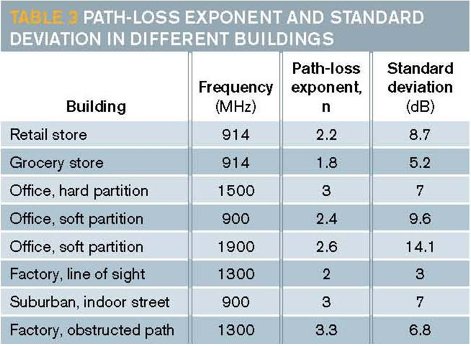
N 的值不會隨著頻率發生太大變化，這個值取決于周圍環境和建筑物類型（見表 3）。

建筑物內的傳播模型包括建筑物類型影響和阻礙。當您僅僅使用一個對數距離模型時，該模型不但提供了靈活性，而且還能夠將測量和預計路徑損耗之間的標準偏差減少至大約 4 dB（與 13 dB 相比）。方程式 17 說明了衰減因數模型：

PL（d）=20log10（fMHz）+10nSFlog10（d）–28+FAF， （17）

方程式中，nSF 表示相同樓層測量的路徑損耗指數值，FAF 則 是樓層衰減因數（見表 3）。您可以從表 2 中確定 FAF 的值。下列的例子演示了怎樣使用前面所述的表以及方程式。例如，如欲計算出戶外空曠環境中距離為 1200 米，頻率為 915 MHz 和 2.4 GHz 時的路徑損耗，則可以使用如下方程式：

20log10（fMHz）+20log10（d）–28， （18）

您在如下情況可以推導出 PL：

915 MHz=“20log10”（915）+20log10（1200） –28=92.8 dB， （19）

以及 PL：

2400 MHz=“20log10”（2400）+20log10（1200） –28=101.2 dB. （20）

高頻傳播會導致更高的路徑損耗，而高路徑損耗又會導致高頻率條件下的無線傳輸距離縮短。例如，同工作在 915 MHz 頻率范圍并且在戶外空曠環境中的設備相比較，工作在 2.4-GHz 頻率范圍的無線設備路徑損耗大約降低了 8.4-dB。

另一個例子中，在同一個樓層及三個樓層里，距離為 100 米、頻率為 915 MHz和 2.4 GHz 的硬分區室內辦公環境下，使用表 2 中的信息來計算出路徑損耗。同一樓層中，通過表 3 可得到該平均路徑損耗為 3 dBm。在以下公式中取 n=“3的值”：

20log10（fMHz）+10log10（d）–28+Xσ， （21）

從而得出 PL 的值：

915 MHz=“20log10”（915）+10（3）log（100） –28+Xσ=91.2 dB， （22）

其中σ=7dB，及 PL：

2400 MHz=“20log10”（2400）+10（3）log （100）–28+Xσ=99.6 dB， （23）

其中σ=14dB

由表 2，您可以計算出三層樓傳播的 FAF 值，大約為24 dB，標準偏差為 5.6 dB。使用以下信息：

20log10（fMHz）+10log10（d）–28+Xσ， （24）

您可以推導出 PL：

915 MHz=“20log10”（915）+10（3）log10（100） –28+24=115.2 dB， （25）

其中 σ=5.6 dB，及 PL

2400 MHz=“20log10”（2400）+ 10（3）log10（100）–28+ 24=123.6 dB， （26）

其中 σ=5.9 dB

在第三個例子中，估算上面兩個例子在頻率為 915 MHz 時的發射距離。在上面兩個例子中假設有一個帶有單位增益傳輸和接收天線的系統，其發射功率為 8 dBm，接收器敏感度為 –100 dBm。系統鏈路預算為 8–（–100）=108 dB。

使用一個值大約為 10dB 的鏈路預算范圍來說明路徑損耗方程式中的標準偏差是一個不錯的主意。從而，得到的鏈路預算為98dB，這一鏈路預算超出了從第一個示例計算得出的值為 92.8dB 的路徑損耗。所以，您可以將 1200 米視為該系統的室外距離。在室內環境下，假設為 10-dB 的范圍（該值超出路徑損耗），那么路徑損耗為 91.2dB，而得到的鏈路預算大約為 98 dB。因此，您可以將 100 米視為該系統的室內距離。

責任編輯：gt