1. 神經網絡的超參數分類
神經網路中的超參數主要包括:
學習率 η,
正則化參數 λ,
神經網絡的層數 L,
每一個隱層中神經元的個數 j ,
學習的回合數Epoch,
小批量數據 minibatch 的大小,
輸出神經元的編碼方式,
代價函數的選擇,
權重初始化的方法,
神經元激活函數的種類,
參加訓練模型數據的規模
這些都是可以影響神經網絡學習速度和最后分類結果,其中神經網絡的學習速度主要根據訓練集上代價函數下降的快慢有關,而最后的分類的結果主要跟在驗證集上的分類正確率有關。因此可以根據該參數主要影響代價函數還是影響分類正確率進行分類。
在上圖中可以看到超參數 2,3,4,7 主要影響的是神經網絡的分類正確率;9主要影響代價函數曲線下降速度,同時有時也會影響正確率;1,8,10 主要影響學習速度,這點主要體現在訓練數據代價函數曲線的下降速度上;
5,6,11 主要影響模型分類正確率和訓練用總體時間。這上面所提到的是某個超參數對于神經網絡想到的首要影響,并不代表著該超參數只影響學習速度或者正確率。因為不同的超參數的類別不同,因此在調整超參數的時候也應該根據對應超參數的類別進行調整。在調整超參數的過程中有根據機理選擇超參數的方法,有根據訓練集上表現情況選擇超參數的方法,也有根據驗證集上訓練數據選擇超參數的方法。他們之間的關系如圖2所示。
超參數 7,8,9,10 由神經網絡的機理進行選擇。在這四個參數中,應該首先對第10個參數神經元的種類進行選擇,根據目前的知識,一種較好的選擇方式是對于神經網絡的隱層采用sigmoid神經元,而對于輸出層采用softmax的方法;
根據輸出層采用sotmax的方法,因此第8個代價函數采用 log-likelihood 函數(或者輸出層還是正常的sigmoid神經元而代價函數為交叉熵函數),第9個初始化權重采用均值為0方差為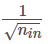 的高斯隨機分布初始化權重;對于輸出層的編碼方式常常采用向量式的編碼方式,基本上不會使用實際的數值或者二進制的編碼方式。
的高斯隨機分布初始化權重;對于輸出層的編碼方式常常采用向量式的編碼方式,基本上不會使用實際的數值或者二進制的編碼方式。
超參數1由訓練數據的代價函數選擇,在上述這兩部分都確定好之后在根據檢驗集數據確定最后的幾個超參數。這只是一個大體的思路,具體每一個參數的確定將在下面具體介紹。
2. 寬泛策略
根據上面的分析我們已經根據機理將神經網絡中的神經元的種類、輸出層的模式(即是否采用softmax)、代價函數及輸出層的編碼方式進行了設定。所以在這四個超參數被確定了之后變需要確定其他的超參數了。
假設我們是從頭開始訓練一個神經網絡的,我們對于其他參數的取值本身沒有任何經驗,所以不可能一上來就訓練一個很復雜的神經網絡,這時就要采用寬泛策略。寬泛策略的核心在于簡化和監控。簡化具體體現在,如簡化我們的問題,如將一個10分類問題轉變為一個2分類問題;簡化網絡的結構,如從一個僅包含10個神經元的隱層開始訓練,逐漸增加網絡的層數和神經元的個數;
簡化訓練用的數據,在簡化問題中,我們已經減少了80%的數據量,在這里我們該要精簡檢驗集中數據的數量,因為真正驗證的是網絡的性能,所以僅用少量的驗證集數據也是可以的,如僅采用100個驗證集數據。
監控具體指的是提高監控的頻率,比如說原來是每5000次訓練返回一次代價函數或者分類正確率,現在每1000次訓練就返回一次。其實可以將“寬泛策略”當作是一種對于網絡的簡單初始化和一種監控策略,這樣可以更加快速地實驗其他的超參數,或者甚至接近同步地進行不同參數的組合的評比。
直覺上看,這看起來簡化問題和架構僅僅會降低你的效率。實際上,這樣能夠將進度加快,因為你能夠更快地找到傳達出有意義的信號的網絡。一旦你獲得這些信號,你可以嘗嘗通過微調超參數獲得快速的性能提升。
3. 學習率的調整
假設我們運行了三個不同學習速率( η=0.025、η=0.25、η=2.5)的 MNIST 網 絡,其他的超參數假設已經設置為進行30回合,minibatch 大小為10,然后 λ=5.0,使用50000幅訓練圖像,訓練代價的變化情況如圖3
使用 η=0.025 ,代價函數平滑下降到最后的回合;使用 η=0.25 ,代價剛開始下降,在大約 20 回合后接近飽和狀態,后面就是微小的震蕩和隨機抖動;最終使用 η=2.5 代價從始至終都震蕩得非常明顯。
因此學習率的調整步驟為:首先,我們選擇在訓練數據上的代價立即開始下降而非震蕩或者增加時的作為 η 閾值的估計,不需要太過精確,確定量級即可。如果代價在訓練的前面若干回合開始下降,你就可以逐步增加 η 的量級,直到你找到一個的值使得在開始若干回合代價就開始震蕩或者增加;
相反,如果代價函數曲線開始震蕩或者增加,那就嘗試減小量級直到你找到代價在開始回合就下降的設定,取閾值的一半就確定了學習速率 。在這里使用訓練數據的原因是學習速率主要的目的是控制梯度下降的步長,監控訓練代價是最好的檢測步長過大的方法。
4. 迭代次數
提前停止表示在每個回合的最后,我們都要計算驗證集上的分類準確率,當準確率不再提升,就終止它也就確定了迭代次數(或者稱回合數)。另外,提前停止也能夠幫助我們避免過度擬合。
我們需要再明確一下什么叫做分類準確率不再提升,這樣方可實現提前停止。正如我們已經看到的,分類準確率在整體趨勢下降的時候仍舊會抖動或者震蕩。如果我們在準確度剛開始下降的時候就停止,那么肯定會錯過更好的選擇。
一種不錯的解決方案是如果分類準確率在一段時間內不再提升的時候終止。建議在更加深入地理解 網絡訓練的方式時,僅僅在初始階段使用 10 回合不提升規則,然后逐步地選擇更久的回合,比如 20 回合不提升就終止,30 回合不提升就終止,以此類推。
5. 正則化參數
我建議,開始時代價函數不包含正則項,只是先確定 η 的值。使用確定出來的 η ,用驗證數據來選擇好的 λ 。嘗試從 λ=1 開始,然后根據驗證集上的性能按照因子 10 增加或減少其值。一旦我已經找到一個好的量級,你可以改進 λ 的值。這里搞定 λ 后,你就可以返回再重新優化 η 。
6. 小批量數據的大小
選擇最好的小批量數據大小也是一種折衷。太小了,你不會用上很好的矩陣庫的快速計算;太大,你是不能夠足夠頻繁地更新權重的。你所需要的是選擇一個折中的值,可以最大化學習的速度。幸運的是,小批量數據大小的選擇其實是相對獨立的一個超參數(網絡整體架構外的參數),所以你不需要優化那些參數來尋找好的小批量數據大小。
因此,可以選擇的方式就是使用某些可以接受的值(不需要是最優的)作為其他參數的選擇,然后進行不同小批量數據大小的嘗試,像上面那樣調整 η 。畫出驗證準確率的值隨時間(非回合)變化的圖,選擇哪個得到最快性能的提升的小批量數據大小。得到了小批量數據大小,也就可以對其他的超參數進行優化了。
7. 總體的調參過程
首先應該根據機理確定激活函數的種類,之后確定代價函數種類和權重初始化的方法,以及輸出層的編碼方式;其次根據“寬泛策略”先大致搭建一個簡單的結構,確定神經網絡中隱層的數目以及每一個隱層中神經元的個數;
然后對于剩下的超參數先隨機給一個可能的值,在代價函數中先不考慮正則項的存在,調整學習率得到一個較為合適的學習率的閾值,取閾值的一半作為調整學習率過程中的初始值 ;
之后通過實驗確定minibatch的大小;之后仔細調整學習率,使用確定出來的 η ,用驗證數據來選擇好的 λ ,搞定 λ 后,你就可以返回再重新優化 η 。而學習回合數可以通過上述這些實驗進行一個整體的觀察再確定。
版權聲明:本文為CSDN博主「獨孤呆博」的原創文章,遵循CC 4.0 BY-SA版權協議,轉載請附上原文出處鏈接及本聲明。
原文鏈接:https://blog.csdn.net/dugudaibo/article/details/77366245
編輯:jq
-
神經網絡
+關注
關注
42文章
4771瀏覽量
100718 -
編碼
+關注
關注
6文章
940瀏覽量
54814 -
函數
+關注
關注
3文章
4327瀏覽量
62573 -
MNIST
+關注
關注
0文章
10瀏覽量
3374
原文標題:如何選擇神經網絡的超參數?
文章出處:【微信號:Imgtec,微信公眾號:Imagination Tech】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
卷積神經網絡的參數調整方法
卷積神經網絡與傳統神經網絡的比較
BP神經網絡和卷積神經網絡的關系
BP神經網絡和人工神經網絡的區別
rnn是遞歸神經網絡還是循環神經網絡
遞歸神經網絡是循環神經網絡嗎
循環神經網絡和卷積神經網絡的區別
深度神經網絡與基本神經網絡的區別
反向傳播神經網絡和bp神經網絡的區別
bp神經網絡和卷積神經網絡區別是什么
BP神經網絡激活函數怎么選擇
卷積神經網絡和bp神經網絡的區別
神經網絡在數學建模中的應用
如何訓練和優化神經網絡
詳解深度學習、神經網絡與卷積神經網絡的應用





 教大家怎么選擇神經網絡的超參數
教大家怎么選擇神經網絡的超參數










評論