密度函數(shù)理論(DFT)已經(jīng)發(fā)展成為電子結(jié)構(gòu)計(jì)算的主要方法,幾乎可以研究材料的所有方面及其特性。大多數(shù)DFT代碼的一個(gè)共同假設(shè)是周期性邊界條件(PBC)。這些條件自然地再現(xiàn)了晶體的平移對(duì)稱性,以描述一個(gè)無(wú)限大的晶體。因此,只需要使用單位晶胞就可高效計(jì)算材料的塊體性質(zhì)。
PBC也可方便地?cái)U(kuò)展到研究平移對(duì)稱性破缺的結(jié)構(gòu)。對(duì)于表面來(lái)說(shuō),平移對(duì)稱性只適用于橫向尺寸,即重復(fù)的slab模型。類似的方法也用于點(diǎn)缺陷和其它缺陷類型。這些方法的共同點(diǎn)是,一個(gè)或多個(gè)無(wú)限的維度是用有限的單元維度來(lái)接近的。因此,獲得準(zhǔn)確結(jié)果的先決條件是仔細(xì)檢查并確保這個(gè)維度的尺寸足夠大,并滿足收斂條件。否則,有限尺寸的誤差可能會(huì)被放大,并對(duì)最終結(jié)果造成巨大誤差。
重復(fù)slab近似方法已成為一類計(jì)算標(biāo)準(zhǔn),通過(guò)DFT計(jì)算和周期性邊界條件準(zhǔn)確描述材料的表面特性。而對(duì)于表現(xiàn)出自發(fā)極化的材料,傳統(tǒng)的贗氫鈍化方法無(wú)法實(shí)現(xiàn)表面的電中性。基于高斯定律,殘余的表面凈電荷會(huì)誘發(fā)可穿越slab的宏觀電場(chǎng),并導(dǎo)致與slab厚度相關(guān)的尺寸收斂性變差。
由德國(guó)馬普所計(jì)算材料部的Su-Hyun Yoo教授和Mira Todorova教授領(lǐng)導(dǎo)的團(tuán)隊(duì),提出了一種方法用以解決在計(jì)算具有自發(fā)極化材料的表面特性(表面態(tài)或表面能量)時(shí),收斂極其緩慢的問(wèn)題。這種極化材料多存在于半導(dǎo)體和絕緣體中。一個(gè)突出的例子是III族氮化物,它是節(jié)能照明的關(guān)鍵材料。
此外,在拓?fù)浣^緣體、光電子和微電子裝置、催化和其他領(lǐng)域的許多氧化物中都具有自發(fā)極化現(xiàn)象。因此,對(duì)于這些在技術(shù)上重要、在科學(xué)上令人興奮的材料系統(tǒng),提出新方法以促進(jìn)尺寸收斂具有重要價(jià)值。
該文近期發(fā)表于npj Computational Materials 7: 58(2021),英文標(biāo)題與摘要如下。
Su-Hyun Yoo, Mira Todorova, Darshana Wickramaratne, Leigh Weston, Chris G. Van de Walle & J?rg Neugebauer
The repeated slab approach has become a de facto standard to accurately describe surface properties of materials by density functional theory calculations with periodic boundary conditions. For materials exhibiting spontaneous polarization,
we show that the conventional scheme of passivation with pseudo hydrogen is unable to realize a charge-neutral surface. The presence of a net surface charge induces via Gauss’s law a macroscopic electric field through the slab and results in poor size convergence with respect to the thickness of the slab.
We propose a modified passivation method that accounts for the effect of spontaneous polarization, describes the correct bulk limits and boosts convergence with respect to slab thickness. The robustness, reliability, and superior convergence of energetics and electronic structure achieved by the proposed method are demonstrated using the example of polar ZnO surfaces.
編輯:jq
-
光電子
+關(guān)注
關(guān)注
1文章
135瀏覽量
17699 - 拓?fù)?/span>
- 函數(shù)
-
DFT
+關(guān)注
關(guān)注
2文章
234瀏覽量
23391 -
絕緣體
+關(guān)注
關(guān)注
1文章
49瀏覽量
5007
原文標(biāo)題:npj: 表面態(tài)計(jì)算—如何消除表面殘余電荷和極化電場(chǎng)?
文章出處:【微信號(hào):zhishexueshuquan,微信公眾號(hào):知社學(xué)術(shù)圈】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
PCB的介質(zhì)損耗角是什么“∠”?
高壓放大器在鐵電陶瓷極化過(guò)程研究中的應(yīng)用
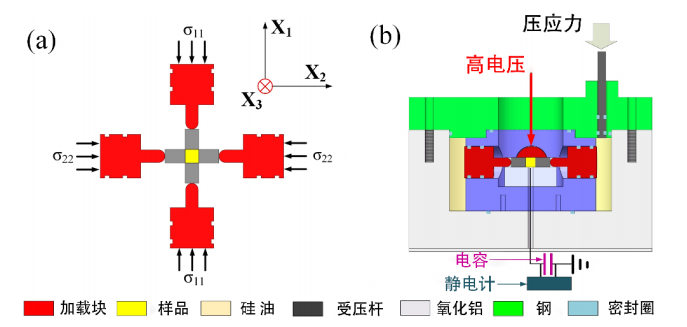
ATA-67100高壓放大器在鐵電材料極化測(cè)試中的應(yīng)用
電荷守恒定律的定義 電荷守恒定律與電場(chǎng)的關(guān)系
帶你了解佰力博FCP薄膜電暈高壓極化儀

無(wú)功補(bǔ)償電容器斷電后內(nèi)部還有殘余電流嗎

優(yōu)化工業(yè)殘余電流監(jiān)測(cè):智能警報(bào)閾值與高效系統(tǒng)保護(hù)
安泰高壓放大器在極化特性及在材料科學(xué)中的應(yīng)用

如何理解差動(dòng)變壓器的零點(diǎn)殘余電壓
差動(dòng)變壓器零點(diǎn)殘余電壓產(chǎn)生原因
安泰高壓放大器在材料極化中的應(yīng)用有哪些




















評(píng)論