很多讀者留言說要看「圖」相關的算法,那就滿足大家,結合算法題把圖相關的技巧給大家過一遍。
前文 學習數據結構的框架思維 說了,數據結構相關的算法無非兩點:遍歷 + 訪問。那么圖的基本遍歷方法也很簡單,前文 圖算法基礎 就講了如何從多叉樹的遍歷框架擴展到圖的遍歷。
圖這種數據結構還有一些比較特殊的算法,比如二分圖判斷,有環圖無環圖的判斷,拓撲排序,以及最經典的最小生成樹,單源最短路徑問題,更難的就是類似網絡流這樣的問題。
不過以我的經驗呢,像網絡流這種問題,你又不是打競賽的,除非自己特別有興趣,否則就沒必要學了;像最小生成樹和最短路徑問題,雖然從刷題的角度用到的不多,但它們屬于經典算法,學有余力可以掌握一下;像拓撲排序這一類,屬于比較基本且有用的算法,應該比較熟練地掌握。
那么本文就結合具體的算法題,來說說拓撲排序算法原理,因為拓撲排序的對象是有向無環圖,所以順帶說一下如何判斷圖是否有環。
判斷有向圖是否存在環
函數簽名如下:
int[] findOrder(int numCourses, int[][] prerequisites);
題目應該不難理解,什么時候無法修完所有課程?當存在循環依賴的時候。
其實這種場景在現實生活中也十分常見,比如我們寫代碼 import 包也是一個例子,必須合理設計代碼目錄結構,否則會出現循環依賴,編譯器會報錯,所以編譯器實際上也使用了類似算法來判斷你的代碼是否能夠成功編譯。
看到依賴問題,首先想到的就是把問題轉化成「有向圖」這種數據結構,只要圖中存在環,那就說明存在循環依賴。
具體來說,我們首先可以把課程看成「有向圖」中的節點,節點編號分別是0, 1, ..., numCourses-1,把課程之間的依賴關系看做節點之間的有向邊。
比如說必須修完課程1才能去修課程3,那么就有一條有向邊從節點1指向3。
所以我們可以根據題目輸入的prerequisites數組生成一幅類似這樣的圖:
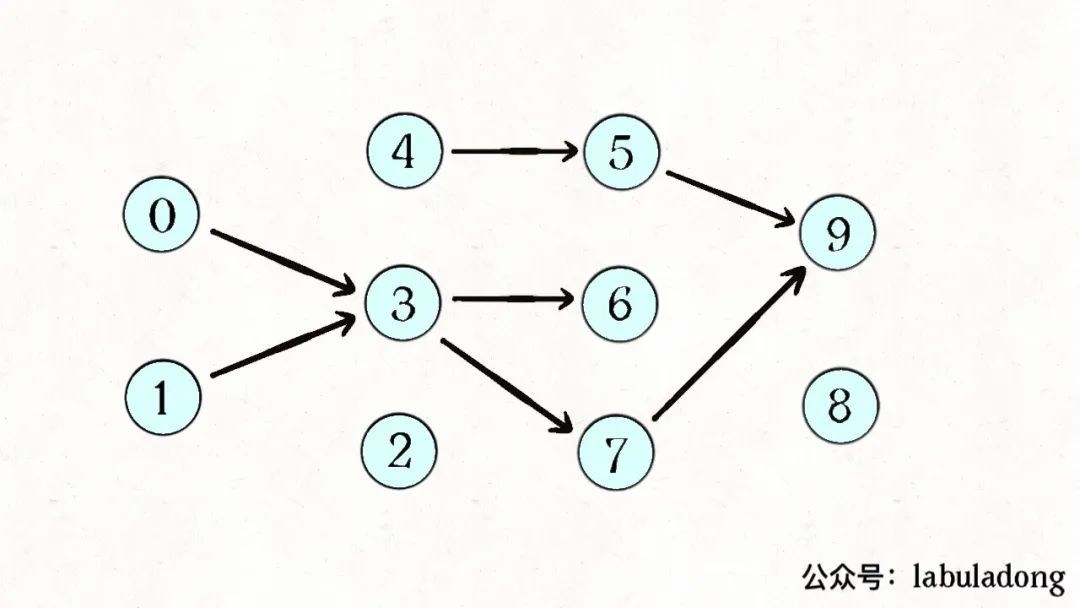
如果發現這幅有向圖中存在環,那就說明課程之間存在循環依賴,肯定沒辦法全部上完;反之,如果沒有環,那么肯定能上完全部課程。
好,那么想解決這個問題,首先我們要把題目的輸入轉化成一幅有向圖,然后再判斷圖中是否存在環。
如何轉換成圖呢?我們前文 圖論基礎 寫過圖的兩種存儲形式,鄰接矩陣和鄰接表。
以我刷題的經驗,常見的存儲方式是使用鄰接表,比如下面這種結構:
List《Integer》[] graph;
graph[s]是一個列表,存儲著節點s所指向的節點。
所以我們首先可以寫一個建圖函數:
List《Integer》[] buildGraph(int numCourses, int[][] prerequisites) {
// 圖中共有 numCourses 個節點
List《Integer》[] graph = new LinkedList[numCourses];
for (int i = 0; i 《 numCourses; i++) {
graph[i] = new LinkedList《》();
}
for (int[] edge : prerequisites) {
int from = edge[1];
int to = edge[0];
// 修完課程 from 才能修課程 to
// 在圖中添加一條從 from 指向 to 的有向邊
graph[from].add(to);
}
return graph;
}
圖建出來了,怎么判斷圖中有沒有環呢?
先不要急,我們先來思考如何遍歷這幅圖,只要會遍歷,就可以判斷圖中是否存在環了。
前文 圖論基礎 寫了 DFS 算法遍歷圖的框架,無非就是從多叉樹遍歷框架擴展出來的,加了個visited數組罷了:
// 防止重復遍歷同一個節點boolean[] visited;
// 從節點 s 開始 BFS 遍歷,將遍歷過的節點標記為 truevoid traverse(List《Integer》[] graph, int s) {
if (visited[s]) {
return;
}
/* 前序遍歷代碼位置 */
// 將當前節點標記為已遍歷
visited[s] = true;
for (int t : graph[s]) {
traverse(graph, t);
}
/* 后序遍歷代碼位置 */
}
那么我們就可以直接套用這個遍歷代碼:
// 防止重復遍歷同一個節點boolean[] visited;
boolean canFinish(int numCourses, int[][] prerequisites) {
List《Integer》[] graph = buildGraph(numCourses, prerequisites);
visited = new boolean[numCourses];
for (int i = 0; i 《 numCourses; i++) {
traverse(graph, i);
}
}
void traverse(List《Integer》[] graph, int s) {
// 代碼見上文
}
注意圖中并不是所有節點都相連,所以要用一個 for 循環將所有節點都作為起點調用一次 DFS 搜索算法。
這樣,就能遍歷這幅圖中的所有節點了,你打印一下visited數組,應該全是 true。
前文 學習數據結構和算法的框架思維 說過,圖的遍歷和遍歷多叉樹差不多,所以到這里你應該都能很容易理解。
那么如何判斷這幅圖中是否存在環呢?
我們前文 回溯算法核心套路詳解 說過,你可以把遞歸函數看成一個在遞歸樹上游走的指針,這里也是類似的:
你也可以把traverse看做在圖中節點上游走的指針,只需要再添加一個布爾數組onPath記錄當前traverse經過的路徑:
boolean[] onPath;
boolean hasCycle = false;
boolean[] visited;
void traverse(List《Integer》[] graph, int s) {
if (onPath[s]) {
// 發現環!!!
hasCycle = true;
}
if (visited[s]) {
return;
}
// 將節點 s 標記為已遍歷
visited[s] = true;
// 開始遍歷節點 s
onPath[s] = true;
for (int t : graph[s]) {
traverse(graph, t);
}
// 節點 s 遍歷完成
onPath[s] = false;
}
這里就有點回溯算法的味道了,在進入節點s的時候將onPath[s]標記為 true,離開時標記回 false,如果發現onPath[s]已經被標記,說明出現了環。
PS:參考貪吃蛇沒繞過彎兒咬到自己的場景。
這樣,就可以在遍歷圖的過程中順便判斷是否存在環了,完整代碼如下:
// 記錄一次 traverse 遞歸經過的節點boolean[] onPath;
// 記錄遍歷過的節點,防止走回頭路boolean[] visited;
// 記錄圖中是否有環boolean hasCycle = false;
boolean canFinish(int numCourses, int[][] prerequisites) {
List《Integer》[] graph = buildGraph(numCourses, prerequisites);
visited = new boolean[numCourses];
onPath = new boolean[numCourses];
for (int i = 0; i 《 numCourses; i++) {
// 遍歷圖中的所有節點
traverse(graph, i);
}
// 只要沒有循環依賴可以完成所有課程
return !hasCycle;
}
void traverse(List《Integer》[] graph, int s) {
if (onPath[s]) {
// 出現環
hasCycle = true;
}
if (visited[s] || hasCycle) {
// 如果已經找到了環,也不用再遍歷了
return;
}
// 前序遍歷代碼位置
visited[s] = true;
onPath[s] = true;
for (int t : graph[s]) {
traverse(graph, t);
}
// 后序遍歷代碼位置
onPath[s] = false;
}
List《Integer》[] buildGraph(int numCourses, int[][] prerequisites) {
// 代碼見前文
}
這道題就解決了,核心就是判斷一幅有向圖中是否存在環。
不過如果出題人繼續惡心你,讓你不僅要判斷是否存在環,還要返回這個環具體有哪些節點,怎么辦?
你可能說,onPath里面為 true 的索引,不就是組成環的節點編號嗎?
不是的,假設下圖中綠色的節點是遞歸的路徑,它們在onPath中的值都是 true,但顯然成環的節點只是其中的一部分:
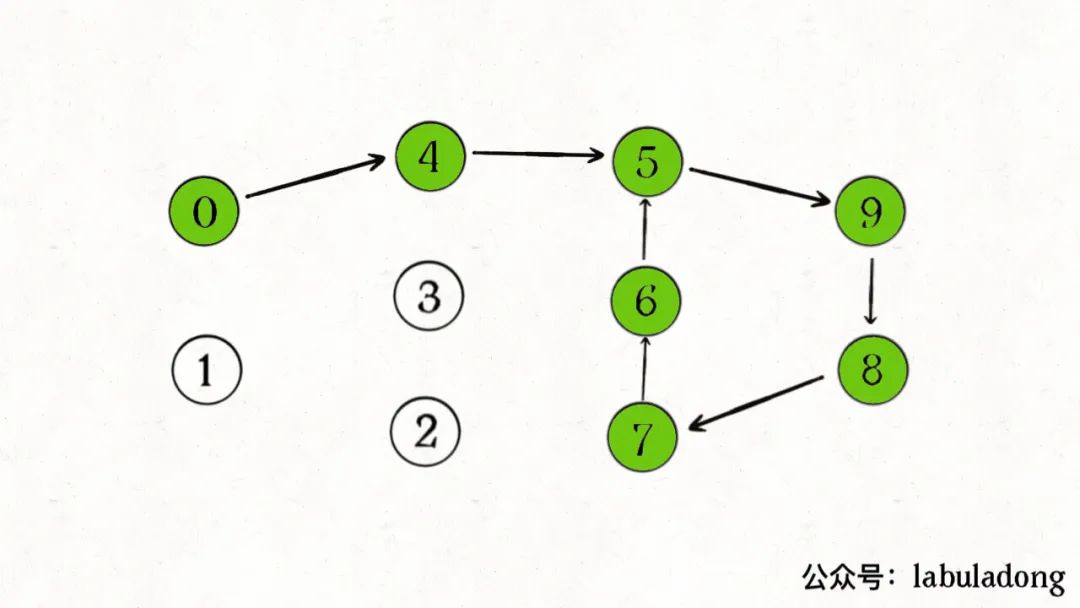
那么接下來,我們來再講一個經典的圖算法:拓撲排序。
拓撲排序
這道題就是上道題的進階版,不是僅僅讓你判斷是否可以完成所有課程,而是進一步讓你返回一個合理的上課順序,保證開始修每個課程時,前置的課程都已經修完。
函數簽名如下:
int[] findOrder(int numCourses, int[][] prerequisites);
這里我先說一下拓撲排序(Topological Sorting)這個名詞,網上搜出來的定義很數學,這里干脆用百度百科的一幅圖來讓你直觀地感受下
直觀地說就是,讓你把一幅圖「拉平」,而且這個「拉平」的圖里面,所有箭頭方向都是一致的,比如上圖所有箭頭都是朝右的。
很顯然,如果一幅有向圖中存在環,是無法進行拓撲排序的,因為肯定做不到所有箭頭方向一致;反過來,如果一幅圖是「有向無環圖」,那么一定可以進行拓撲排序。
但是我們這道題和拓撲排序有什么關系呢?
其實也不難看出來,如果把課程抽象成節點,課程之間的依賴關系抽象成有向邊,那么這幅圖的拓撲排序結果就是上課順序。
首先,我們先判斷一下題目輸入的課程依賴是否成環,成環的話是無法進行拓撲排序的,所以我們可以復用上一道題的主函數:
public int[] findOrder(int numCourses, int[][] prerequisites) {
if (!canFinish(numCourses, prerequisites)) {
// 不可能完成所有課程
return new int[]{};
}
// 。..
}
PS:簡單起見,canFinish 直接復用了之前實現的函數,但實際上可以把環檢測的邏輯和拓撲排序的邏輯結合起來,同時在 traverse 函數里完成,這個可以留給大家自己去實現。
那么關鍵問題來了,如何進行拓撲排序?是不是又要秀什么高大上的技巧了?
其實特別簡單,將后序遍歷的結果進行反轉,就是拓撲排序的結果。
直接看解法代碼:
boolean[] visited;
// 記錄后序遍歷結果
List《Integer》 postorder = new ArrayList《》();
int[] findOrder(int numCourses, int[][] prerequisites) {
// 先保證圖中無環
if (!canFinish(numCourses, prerequisites)) {
return new int[]{};
}
// 建圖
List《Integer》[] graph = buildGraph(numCourses, prerequisites);
// 進行 DFS 遍歷
visited = new boolean[numCourses];
for (int i = 0; i 《 numCourses; i++) {
traverse(graph, i);
}
// 將后序遍歷結果反轉,轉化成 int[] 類型
Collections.reverse(postorder);
int[] res = new int[numCourses];
for (int i = 0; i 《 numCourses; i++) {
res[i] = postorder.get(i);
}
return res;
}
void traverse(List《Integer》[] graph, int s) {
if (visited[s]) {
return;
}
visited[s] = true;
for (int t : graph[s]) {
traverse(graph, t);
}
// 后序遍歷位置
postorder.add(s);
}
// 參考上一題的解法boolean canFinish(int numCourses, int[][] prerequisites);
// 參考前文代碼
List《Integer》[] buildGraph(int numCourses, int[][] prerequisites);
代碼雖然看起來多,但是邏輯應該是很清楚的,只要圖中無環,那么我們就調用traverse函數對圖進行 BFS 遍歷,記錄后序遍歷結果,最后把后序遍歷結果反轉,作為最終的答案。
那么為什么后序遍歷的反轉結果就是拓撲排序呢?
我這里也避免數學證明,用一個直觀地例子來解釋,我們就說二叉樹,這是我們說過很多次的二叉樹遍歷框架:
void traverse(TreeNode root) {
// 前序遍歷代碼位置
traverse(root.left)
// 中序遍歷代碼位置
traverse(root.right)
// 后序遍歷代碼位置
}
二叉樹的后序遍歷是什么時候?遍歷完左右子樹之后才會執行后序遍歷位置的代碼。換句話說,當左右子樹的節點都被裝到結果列表里面了,根節點才會被裝進去。
后序遍歷的這一特點很重要,之所以拓撲排序的基礎是后序遍歷,是因為一個任務必須在等到所有的依賴任務都完成之后才能開始開始執行。
你把每個任務理解成二叉樹里面的節點,這個任務所依賴的任務理解成子節點,那你是不是應該先把所有子節點處理完再處理父節點?這是不是就是后序遍歷?
下圖是一個二叉樹的后序遍歷結果:
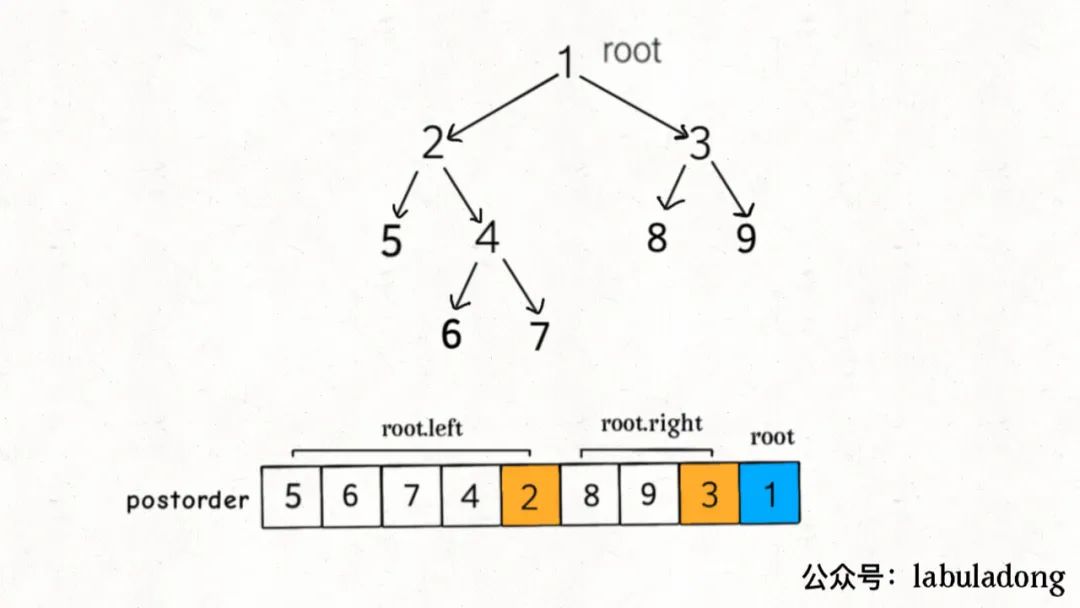
結合這個圖說一說為什么還要把后序遍歷結果反轉,才是最終的拓撲排序結果。
我們說一個節點可以理解為一個任務,這個節點的子節點理解為這個任務的依賴,但你注意我們之前說的依賴關系的表示:如果做完A才能去做B,那么就有一條從A指向B的有向邊,表示B依賴A。
那么,父節點依賴子節點,體現在二叉樹里面應該是這樣的
是不是和我們正常的二叉樹指針指向反過來了?所以正常的后序遍歷結果應該進行反轉,才是拓撲排序的結果。
以上,我簡單解釋了一下為什么「拓撲排序的結果就是反轉之后的后序遍歷結果」,當然,我的解釋雖然比較直觀,但并沒有嚴格的數學證明,有興趣的讀者可以自己查一下。
總之,你記住拓撲排序就是后序遍歷反轉之后的結果,且拓撲排序只能針對有向無環圖,進行拓撲排序之前要進行環檢測,這些知識點已經足夠了。
責任編輯:haq
-
數據
+關注
關注
8文章
7067瀏覽量
89108 -
拓撲結構
+關注
關注
6文章
324瀏覽量
39217
原文標題:拓撲排序,YYDS!
文章出處:【微信號:xincailiaozaixian,微信公眾號:新材料在線】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
TimSort:一個在標準函數庫中廣泛使用的排序算法
【「從算法到電路—數字芯片算法的電路實現」閱讀體驗】+內容簡介
時間復雜度為 O(n^2) 的排序算法

FPGA實現雙調排序算法的探索與實踐

想聽聽48和大對數光纜的排序?
C語言實現經典排序算法概覽





 拓撲排序算法原理是什么
拓撲排序算法原理是什么













評論