跳躍鏈表及其應用是非常熱門的問題,面試時也非常常問,深入了解其中奧秘大有裨益,不吹了,直接開始!
跳躍鏈表的基本概念
初識跳表
跳躍列表是一種數據結構。它允許快速查詢一個有序連續元素的數據鏈表。跳躍列表的平均查找和插入時間復雜度都是O(log n),優于普通隊列的O(n)。
跳躍列表由威廉·普發明,發明者對跳躍列表的評價:跳躍鏈表是在很多應用中有可能替代平衡樹而作為實現方法的一種數據結構。
跳躍列表的算法有同平衡樹一樣的漸進的預期時間邊界,并且更簡單、更快速和使用更少的空間。
這種數據結構是由William Pugh(音譯為威廉·普)發明的,最早出現于他在1990年發表的論文《Skip Lists: A Probabilistic Alternative to Balanced Trees》。
我在谷歌上找到一篇作者關于跳表的論文,感興趣強烈建議下載閱讀:
https://epaperpress.com/sortsearch/download/skiplist.pdf
從中我們獲取到的信息是:跳表在動態查找過程中使用了一種非嚴格的平衡機制來讓插入和刪除都更加便利和快捷,這種非嚴格平衡是基于概率的,而不是平衡樹的嚴格平衡。
說到非嚴格平衡,首先想到的是紅黑樹RbTree,它同樣采用非嚴格平衡來避免像AVL那樣調整樹的結構,這里就不展開講紅黑樹了,看來跳表也是類似的路子,但是是基于概率實現的。
動態查找的數據結構
所謂動態查找就是查找的過程中存在元素的刪除和插入,這樣就對實現查找的數據結構有一定的挑戰,因為在每次刪除和插入時都要調整數據結構,來保持秩序。
可以作為查找數據結構的包括:
線性結構:數組、鏈表
非線性結構:平衡樹
來分析一下各種數據結構在應對動態查找時的優劣吧!
數組結構
數組結構簡單內存連續,可以實現二分查找等基于下標的操作,我一直認為數組的殺手锏就是下標,連續的內存也帶來了問題。
當進行插入和刪除時就面臨著整體的調整,就像在火車站排隊買票,隊頭走一個整個隊伍向前挪一步,有加塞的后面的又整體向后挪一步,這種整體移動操作在數組結構中性能損耗很大,并且在大數據量時對連續內存要求很高,當然這個在大內存機器上可能沒有什么問題。
如圖插入6和刪除5時 數組元素的移動:
鏈表結構
鏈表結構也比較簡單,但是不要求內存連續,不連續也就沒有下標可以加速,但是鏈表在執行刪除和插入時影響的只是插入刪除點的前后元素,影響非常小。
但是每次查找元素是需要進行遍歷,就算我知道某個元素一定在大致的什么位置,也只能一步步走過去,看到這里要覺得有優化的空間,那你也蠻厲害的了,說不定早幾年跳表就是你的發明了。
如圖刪除元素5和插入元素49時的處理:
平衡樹
平衡樹也是處理動態查找問題的一把好手,樹一般是基于鏈表實現的,只不過樹的節點之間并不是鏈表簡單的線性關系,會有兄弟姐妹父親等節點,并且各個層級有數量的限制,可以看到樹其實還是蠻復雜的。
節點需要存儲的信息很多,各個指針指來指去,復雜的結構增加了調整平衡性的難度,不同情況下的左旋右旋,所以出現了紅黑樹這種工程版本的AVL,但是在實際場景中可能并不需要這些兄弟姐妹父親關系,有種殺雞宰牛刀的意味了。
紅黑樹的節點結構定義:
#define COLOR_RED 0x0#define COLOR_BLACK 0x1
typedef struct RBNode{
int key;
unsigned char color;
struct RBNode *left;
struct RBNode *right;
struct RBNode *parent;
}rb_node_t, *rb_tree_t;
另外紅黑樹調整屬性過程中插入分為3種情況,刪除分為4種情況,還是比較難以理解的,除非你穿紅上衣&黑褲子來瘋狂暗示面試官,要不然被問到的概率還不太大。
三種結構對比
從上面的對比可以看到:數組并不能很好滿足要求,鏈表在搜索過程又顯得更笨拙,平衡樹又有點復雜,到底該怎么辦?
跳表的雛形
上面的三類結構都存在一些問題,所以要進行改造,可以看到數組和平衡樹的某些特性決定了它們不容易被改造(數組內存連續性、平衡樹節點多指針和層級關系),相反鏈表最有潛力被改造優化。
在有序鏈表中插入和刪除都比較簡單,搜索時無法依靠下標只能遍歷,但是明明知道要走兩步可以到達目的地,偏偏只能一步步走,這就是痛點。
如圖演示了O(n)遍歷元素35和跳躍搜索元素35的過程:
貌似看到了曙光,那么如何實現跳躍呢?
沒錯!給鏈表加索引,讓索引告訴我們下一步該跳到哪里。
看到這里又讓我想起來那個經典的中間層理論,遇到問題,試著加個中間層試試,或許就完美解決了。
跳躍鏈表的實現原理
前面說了可以給普通鏈表加索引來解決,但是具體該怎么操作,以及其中有什么難點?一步步來分析。
在工程中對跳表索引層數和結點是否作為索引結點,是其很重要的屬性,后面就詳細講一下,現在先看一種簡單場景,說明索引帶來的便利性。
簡單的索引
選擇每隔1個結點為索引結點,并且索引為一層,雖然在工程中這種形式比較標準化,不過足以說明索引帶來的加速。
可以將鏈表中的偶數序號節點增加一層指針,讓其指向下一個偶數節點,如圖所示:
搜索過程:
加入要搜索值為55的節點,則先在上層進行搜索,由16跳到38,在38的下一跳將到達72,因此向下降一級繼續類似的搜索,則找到55。
多級索引
基于偶數節點增加索引并且只有兩層的情況下,最高層的節點數是n/2,整體來看搜索的復雜度降低為O(n/2),并不要小看這個1/2的系數,看到這里會想 增加索引層數到k,那么復雜度將指數降低為O(n/2^k)。
索引層數不是無休止增加的,取決于該層索引的節點數量,如果該層的索引的節點數量等于2了,那么再往上加層也就沒有意義了,畫個圖看一下:
這個非常好理解,如果所在層索引結點只有1個,比如4層索引的結點16,只能順著16向下遍歷,無法向后跳到4層其他結點,因此當所在層索引結點數量等于2,則到達最高索引層,這個約束在分析跳表復雜度時很重要。
索引層數和索引結點密度
跳表的復雜度和索引層數、索引結點的稀疏程度有很大關系。
索引層數我們從上面也看到了,稀疏程度相當于索引結點的數量比例,如果跳表的索引結點數量很少,那么將接近退化為普通鏈表,這種情況在數據量是較大時非常明顯,畫圖看下(藍色部分表示有很多結點):
圖中可以看到雖然有索引層,但是索引結點數量相對全部數據比例較低,這種情況下搜索35相比無索引情況優勢并不明顯。
所以跳表的效率和索引層數和索引結點的密度有密切的關系,當然索引結點太多也就等于沒有索引了。
太少的索引結點和太多的索引結點都是一樣的低效。
復雜度分析
從前面的分析可知,跳表的復雜度和索引層數m以及索引結點間隙d有直接關系,其中索引結點間隙理解為相隔幾個結點出現索引結點,體現了對應層索引結點的稀疏程度,在無索引結點時只能遍歷無法跳躍。
如何確定最高索引層數m呢?
如果一個鏈表有 n 個結點,如果每兩個結點取出一個結點建立索引,那么第一級索引的結點數是 n/2,第二級索引的結點數是n/4,以此類推第 m 級索引的結點數為 n/(2^m),前面說過最高層結點數為2,因此存在關系:
算上最底層的原始鏈表,整個跳表的高度為h=logn(底數為2),每一層需要遍歷的結點數是d,那么整個過程的復雜度為:O(d*logn)。
d表明了層間結點的稀疏程度,也就是每隔2個結點選取索引結點、或者每隔3個結點選取索引結點,每個4個結點選取索引結點。..。..
最密集的情況下d=2,借用知乎某大佬的文章的圖片:
但是索引結點密集也意味著存儲空間的增加,跳表相比較普通鏈表就是典型的用空間換時間的數據結構,這樣就達到了AVL的復雜度O(logn)。
跳表的空間存儲
以d=2的最密集情況為例,計算跳表的索引結點總數:2+4+8+.。..。.n/8+n/4+n/2=n-2
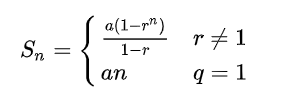
由等比數列求和公式得d=2的跳表額外空間為O(n-2)。
跳表的插入和刪除
工程中的跳表并不嚴格要求索引層結點數量遵循2:1的關系,因為這種要求將導致插入和刪除數據時的調整,成本很大。
跳表的每個插入的結點在插入時進行選擇是否作為索引結點,如果作為索引結點則隨機出層數,整個過程都是基于概率的,但是在大數據量時卻能很好地解決索引層數和結點數的權衡。
我們針對插入和刪除來看下基本的操作過程吧!
跳表元素17插入:
鏈表的插入和刪除是結合搜索過程完成的,貼一張William Pugh在論文中給出的在跳表中插入元素17的過程圖(暫時忽略結點17是否作為索引結點以及索引層數,后面會詳細說明):
跳表元素1刪除:
跳表元素的刪除與普通鏈表相比增加了索引層的判斷,如果結點是非索引結點則正常處理,如果結點是索引結點那邊需要進行索引層結點的處理。
跳躍鏈表的應用
一般討論查找問題時首先想到的是平衡樹和哈希表,但是跳表這種數據結構也非常犀利,性能和實現復雜度都可以和紅黑樹媲美,甚至某些場景由于紅黑樹,從1990年被發明目前廣泛應用于多種場景中,包括Redis、LevelDB等數據存儲引擎中,后續將詳細介紹。
跳表在Redis中的應用
ZSet結構同時包含一個字典和一個跳躍表,跳躍表按score從小到大保存所有集合元素。字典保存著從member到score的映射。這兩種結構通過指針共享相同元素的member和score,不會浪費額外內存。
typedef struct zset {
dict *dict;
zskiplist *zsl;
} zset;
ZSet中的字典和跳表布局:
ZSet中跳表的實現細節
隨機層數的實現原理
跳表是一個概率型的數據結構,元素的插入層數是隨機指定的。Willam Pugh在論文中描述了它的計算過程如下:指定節點最大層數 MaxLevel,指定概率 p, 默認層數 lvl 為1
生成一個0~1的隨機數r,若r《p,且lvl《MaxLevel ,則lvl ++
重復第 2 步,直至生成的r 》p 為止,此時的 lvl 就是要插入的層數。
論文中生成隨機層數的偽碼:
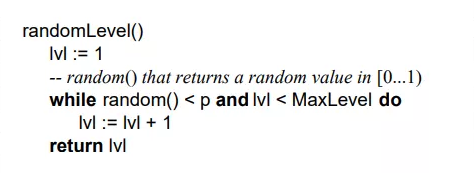
在Redis中對跳表的實現基本上也是遵循這個思想的,只不過有微小差異,看下Redis關于跳表層數的隨機源碼src/z_set.c:
/* Returns a random level for the new skiplist node we are going to create.
* The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
* (both inclusive), with a powerlaw-alike distribution where higher
* levels are less likely to be returned. */
int zslRandomLevel(void) {
int level = 1;
while ((random()&0xFFFF) 《 (ZSKIPLIST_P * 0xFFFF))
level += 1;
return (level《ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}
其中兩個宏的定義在redis.h中:
#define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^32 elements */#define ZSKIPLIST_P 0.25 /* Skiplist P = 1/4 */
可以看到while中的:
(random()&0xFFFF) 《 (ZSKIPLIST_P*0xFFFF)
第一眼看到這個公式,因為涉及位運算有些詫異,需要研究一下Antirez為什么使用位運算來這么寫?
最開始的猜測是random()返回的是浮點數[0-1],于是乎在線找了個浮點數轉二進制的工具,輸入0.5看了下結果:
可以看到0.5的32bit轉換16進制結果為0x3f000000,如果與0xFFFF做與運算結果還是0,不符合預期。
我印象中C語言的math庫好像并沒有直接random函數,所以就去Redis源碼中找找看,于是下載了3.2版本代碼,也并沒有找到random()的實現,不過找到了其他幾個地方的應用:
random()在dict.c中的使用:
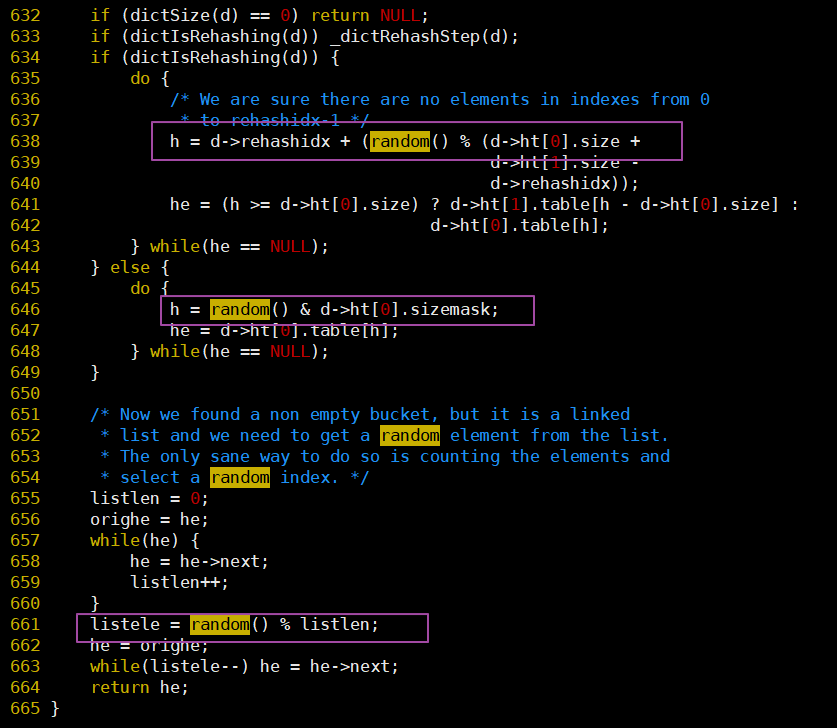
random()在cluster.c中的使用:
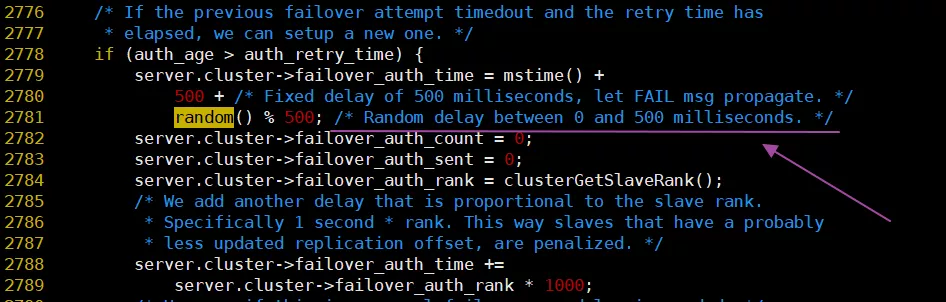
看到這里的取模運算,后知后覺地發現原以為random()是個[0-1]的浮點數,但是現在看來是uint32才對,這樣Antirez的式子就好理解了。
ZSKIPLIST_P*0xFFFF
由于ZSKIPLIST_P=0.25,所以相當于0xFFFF右移2位變為0x3FFF,假設random()比較均勻,在進行0xFFFF高16位清零之后,低16位取值就落在0x0000-0xFFFF之間,這樣while為真的概率只有1/4,更一般地說為真的概率為1/ZSKIPLIST_P。
對于隨機層數的實現并不統一,重要的是隨機數的生成,在LevelDB中對跳表層數的生成代碼是這樣的:
template 《typename Key, typename Value》
int SkipList《Key, Value》::randomLevel() {
static const unsigned int kBranching = 4;
int height = 1;
while (height 《 kMaxLevel && ((::Next(rnd_) % kBranching) == 0)) {
height++;
}
assert(height 》 0);
assert(height 《= kMaxLevel);
return height;
}
uint32_t Next( uint32_t& seed) {
seed = seed & 0x7fffffffu;
if (seed == 0 || seed == 2147483647L) {
seed = 1;
}
static const uint32_t M = 2147483647L;
static const uint64_t A = 16807;
uint64_t product = seed * A;
seed = static_cast《uint32_t》((product 》》 31) + (product & M));
if (seed 》 M) {
seed -= M;
}
return seed;
}
可以看到leveldb使用隨機數與kBranching取模,如果值為0就增加一層,這樣雖然沒有使用浮點數,但是也實現了概率平衡。
跳表結點的平均層數
我們很容易看出,產生越高的節點層數出現概率越低,無論如何層數總是滿足冪次定律越大的數出現的概率越小。
如果某件事的發生頻率和它的某個屬性成冪關系,那么這個頻率就可以稱之為符合冪次定律。
冪次定律的表現是少數幾個事件的發生頻率占了整個發生頻率的大部分, 而其余的大多數事件只占整個發生頻率的一個小部分。
冪次定律應用到跳表的隨機層數來說就是大部分的節點層數都是黃色部分,只有少數是綠色部分,并且概率很低。
定量的分析如下:
節點層數至少為1,大于1的節點層數滿足一個概率分布。
節點層數恰好等于1的概率為p^0(1-p)
節點層數恰好等于2的概率為p^1(1-p)
節點層數恰好等于3的概率為p^2(1-p)
節點層數恰好等于4的概率為p^3(1-p)
依次遞推節點層數恰好等于K的概率為p^(k-1)(1-p)
因此如果我們要求節點的平均層數,那么也就轉換成了求概率分布的期望問題了,靈魂畫手的我再次上線:
表中P為概率,V為對應取值,給出了所有取值和概率的可能,因此就可以求這個概率分布的期望了。
方括號里面的式子其實就是高一年級學的等比數列,常用技巧錯位相減求和,從中可以看到結點層數的期望值與1-p成反比。
對于Redis而言,當p=0.25時結點層數的期望是1.33。
在Redis源碼中有詳盡的關于插入和刪除調整跳表的過程,本文就不再展開了,代碼并不算難懂,都是純C寫的沒有那么多炫技的特效,放心大膽讀起來。
小結
本文主要講述了跳表的基本概念和簡單原理、以及索引結點層級、時間和空間復雜度等相關部分,并沒有涉及概率平衡以及工程實現部分,并且以Redis中底層的數據結構zset作為典型應用來展開,進一步看到跳躍鏈表的實際應用。
需要注意的是跳躍鏈表的原理、應用、實現細節也是面試的熱點問題,值得大家花費時間來研究掌握。
責任編輯:haq
-
數據
+關注
關注
8文章
7002瀏覽量
88943 -
鏈表
+關注
關注
0文章
80瀏覽量
10558
原文標題:20 張圖擊潰,跳表!
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
X電容和Y電容的基本概念
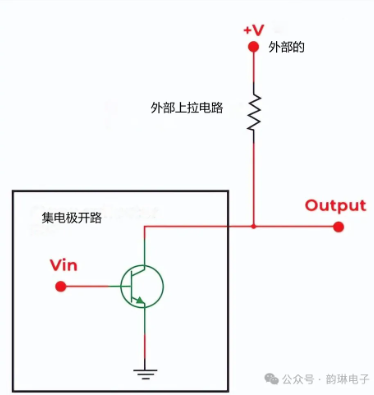
集電極開路的基本概念與原理
DDR4的基本概念和特性
伺服系統基本概念和與變頻的關系
socket的基本概念和原理
BP網絡的基本概念和訓練原理
卷積神經網絡的基本概念、原理及特點
循環神經網絡的基本概念
卷積神經網絡的基本概念和工作原理
組合邏輯控制器的基本概念、實現原理及設計方法
濾波器的作用與分類詳解:從基本概念到實際應用!

電源路徑的基本概念




 跳表的基本概念和實際應用
跳表的基本概念和實際應用












評論