讀完本文，可以去力扣解決如下題目：

743. 網(wǎng)絡(luò)延遲時間（中等）

1514. 概率最大的路徑（中等）

1631. 最小體力消耗路徑（中等）

其實(shí)，很多算法的底層原理異常簡單，無非就是一步一步延伸，變得看起來好像特別復(fù)雜，特別牛逼。

但如果你看過歷史文章，應(yīng)該可以對算法形成自己的理解，就會發(fā)現(xiàn)很多算法都是換湯不換藥，毫無新意，非常枯燥。

比如，我們說二叉樹非常重要，你把這個結(jié)構(gòu)掌握了，就會發(fā)現(xiàn) 動態(tài)規(guī)劃，分治算法，回溯（DFS）算法，BFS 算法框架，Union-Find 并查集算法，二叉堆實(shí)現(xiàn)優(yōu)先級隊列 就是把二叉樹翻來覆去的運(yùn)用。

那么本文又要告訴你，Dijkstra 算法（一般音譯成迪杰斯特拉算法）無非就是一個 BFS 算法的加強(qiáng)版，它們都是從二叉樹的層序遍歷衍生出來的。

這也是為什么我在 學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)和算法的框架思維 中這么強(qiáng)調(diào)二叉樹的原因。

下面我們由淺入深，從二叉樹的層序遍歷聊到 Dijkstra 算法，給出 Dijkstra 算法的代碼框架，順手秒殺幾道運(yùn)用 Dijkstra 算法的題目。

圖的抽象

前文 圖論第一期：遍歷基礎(chǔ) 說過「圖」這種數(shù)據(jù)結(jié)構(gòu)的基本實(shí)現(xiàn)，圖中的節(jié)點(diǎn)一般就抽象成一個數(shù)字（索引），圖的具體實(shí)現(xiàn)一般是「鄰接矩陣」或者「鄰接表」。

比如上圖這幅圖用鄰接表和鄰接矩陣的存儲方式如下：

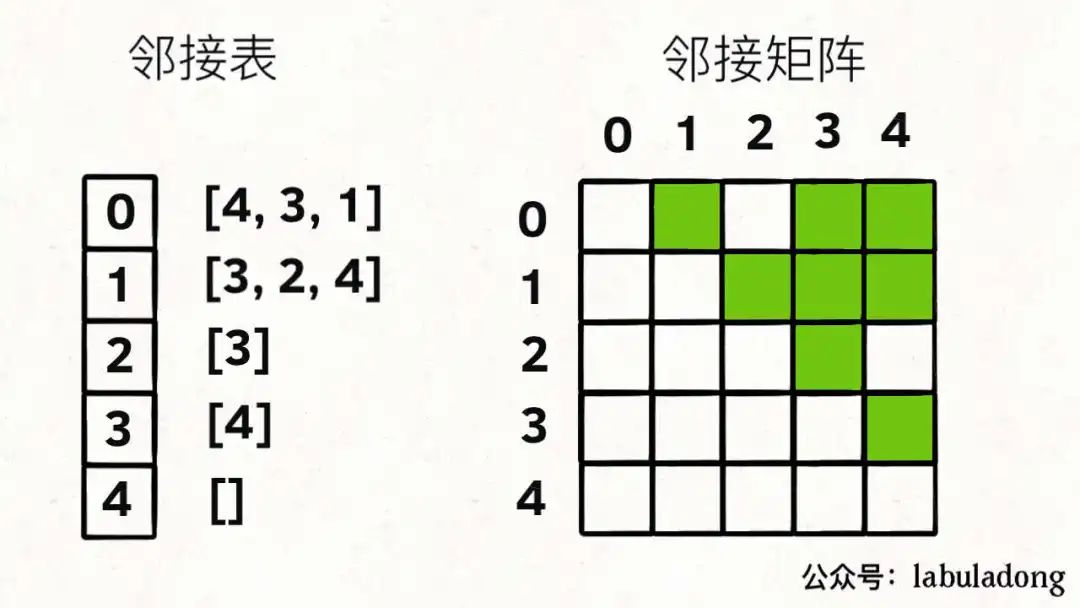
前文 圖論第二期：拓?fù)渑判?告訴你，我們用鄰接表的場景更多，結(jié)合上圖，一幅圖可以用如下 Java 代碼表示：

// graph［s］ 存儲節(jié)點(diǎn) s 指向的節(jié)點(diǎn)（出度）

List《Integer》［］ graph;

如果你想把一個問題抽象成「圖」的問題，那么首先要實(shí)現(xiàn)一個 APIadj：

// 輸入節(jié)點(diǎn) s 返回 s 的相鄰節(jié)點(diǎn)List《Integer》 adj（int s）;

類似多叉樹節(jié)點(diǎn)中的children字段記錄當(dāng)前節(jié)點(diǎn)的所有子節(jié)點(diǎn)，adj（s）就是計算一個節(jié)點(diǎn)s的相鄰節(jié)點(diǎn)。

比如上面說的用鄰接表表示「圖」的方式，adj函數(shù)就可以這樣表示：

List《Integer》［］ graph;

// 輸入節(jié)點(diǎn) s，返回 s 的相鄰節(jié)點(diǎn)List《Integer》 adj（int s） {

return graph［s］;

}

當(dāng)然，對于「加權(quán)圖」，我們需要知道兩個節(jié)點(diǎn)之間的邊權(quán)重是多少，所以還可以抽象出一個weight方法：

// 返回節(jié)點(diǎn) from 到節(jié)點(diǎn) to 之間的邊的權(quán)重int weight（int from， int to）;

這個weight方法可以根據(jù)實(shí)際情況而定，因?yàn)椴煌乃惴}，題目給的「權(quán)重」含義可能不一樣，我們存儲權(quán)重的方式也不一樣。

有了上述基礎(chǔ)知識，就可以搞定 Dijkstra 算法了，下面我給你從二叉樹的層序遍歷開始推演出 Dijkstra 算法的實(shí)現(xiàn)。

二叉樹層級遍歷和 BFS 算法

我們之前說過二叉樹的層級遍歷框架：

// 輸入一棵二叉樹的根節(jié)點(diǎn)，層序遍歷這棵二叉樹void levelTraverse（TreeNode root） {

if （root == null） return 0;

Queue《TreeNode》 q = new LinkedList《》（）;

q.offer（root）;

int depth = 1;

// 從上到下遍歷二叉樹的每一層

while （！q.isEmpty（）） {

int sz = q.size（）;

// 從左到右遍歷每一層的每個節(jié)點(diǎn)

for （int i = 0; i 《 sz; i++） {

TreeNode cur = q.poll（）;

printf（“節(jié)點(diǎn) %s 在第 %s 層”， cur， depth）;

// 將下一層節(jié)點(diǎn)放入隊列

if （cur.left ！= null） {

q.offer（cur.left）;

}

if （cur.right ！= null） {

q.offer（cur.right）;

}

}

depth++;

}

}

我們先來思考一個問題，注意二叉樹的層級遍歷while循環(huán)里面還套了個for循環(huán)，為什么要這樣？

while循環(huán)和for循環(huán)的配合正是這個遍歷框架設(shè)計的巧妙之處

while循環(huán)控制一層一層往下走，for循環(huán)利用sz變量控制從左到右遍歷每一層二叉樹節(jié)點(diǎn)。

注意我們代碼框架中的depth變量，其實(shí)就記錄了當(dāng)前遍歷到的層數(shù)。換句話說，每當(dāng)我們遍歷到一個節(jié)點(diǎn)cur，都知道這個節(jié)點(diǎn)屬于第幾層。

算法題經(jīng)常會問二叉樹的最大深度呀，最小深度呀，層序遍歷結(jié)果呀，等等問題，所以記錄下來這個深度depth是有必要的。

基于二叉樹的遍歷框架，我們又可以擴(kuò)展出多叉樹的層序遍歷框架：

// 輸入一棵多叉樹的根節(jié)點(diǎn)，層序遍歷這棵多叉樹void levelTraverse（TreeNode root） {

if （root == null） return 0;

Queue《TreeNode》 q = new LinkedList《》（）;

q.offer（root）;

int depth = 1;

// 從上到下遍歷多叉樹的每一層

while （！q.isEmpty（）） {

int sz = q.size（）;

// 從左到右遍歷每一層的每個節(jié)點(diǎn)

for （int i = 0; i 《 sz; i++） {

TreeNode cur = q.poll（）;

printf（“節(jié)點(diǎn) %s 在第 %s 層”， cur， depth）;

// 將下一層節(jié)點(diǎn)放入隊列

for （TreeNode child ： root.children） {

q.offer（child）;

}

}

depth++;

}

}

基于多叉樹的遍歷框架，我們又可以擴(kuò)展出 BFS（廣度優(yōu)先搜索）的算法框架：

// 輸入起點(diǎn)，進(jìn)行 BFS 搜索int BFS（Node start） {

Queue《Node》 q; // 核心數(shù)據(jù)結(jié)構(gòu)

Set《Node》 visited; // 避免走回頭路

q.offer（start）; // 將起點(diǎn)加入隊列

visited.add（start）;

int step = 0; // 記錄搜索的步數(shù)

while （q not empty） {

int sz = q.size（）;

/* 將當(dāng)前隊列中的所有節(jié)點(diǎn)向四周擴(kuò)散一步 */

for （int i = 0; i 《 sz; i++） {

Node cur = q.poll（）;

printf（“從 %s 到 %s 的最短距離是 %s”， start， cur， step）;

/* 將 cur 的相鄰節(jié)點(diǎn)加入隊列 */

for （Node x ： cur.adj（）） {

if （x not in visited） {

q.offer（x）;

visited.add（x）;

}

}

}

step++;

}

}

如果對 BFS 算法不熟悉，可以看前文 BFS 算法框架，這里只是為了讓你做個對比，所謂 BFS 算法，就是把算法問題抽象成一幅「無權(quán)圖」，然后繼續(xù)玩二叉樹層級遍歷那一套罷了。

注意，我們的 BFS 算法框架也是while循環(huán)嵌套for循環(huán)的形式，也用了一個step變量記錄for循環(huán)執(zhí)行的次數(shù)，無非就是多用了一個visited集合記錄走過的節(jié)點(diǎn)，防止走回頭路罷了。

為什么這樣呢？

所謂「無權(quán)圖」，與其說每條「邊」沒有權(quán)重，不如說每條「邊」的權(quán)重都是 1，從起點(diǎn)start到任意一個節(jié)點(diǎn)之間的路徑權(quán)重就是它們之間「邊」的條數(shù)，那可不就是step變量記錄的值么？

再加上 BFS 算法利用for循環(huán)一層一層向外擴(kuò)散的邏輯和visited集合防止走回頭路的邏輯，當(dāng)你每次從隊列中拿出節(jié)點(diǎn)cur的時候，從start到cur的最短權(quán)重就是step記錄的步數(shù)。

但是，到了「加權(quán)圖」的場景，事情就沒有這么簡單了，因?yàn)槟悴荒苣J(rèn)每條邊的「權(quán)重」都是 1 了，這個權(quán)重可以是任意正數(shù)（Dijkstra 算法要求不能存在負(fù)權(quán)重邊），比如下圖的例子：

如果沿用 BFS 算法中的step變量記錄「步數(shù)」，顯然紅色路徑一步就可以走到終點(diǎn)，但是這一步的權(quán)重很大；正確的最小權(quán)重路徑應(yīng)該是綠色的路徑，雖然需要走很多步，但是路徑權(quán)重依然很小。

其實(shí) Dijkstra 和 BFS 算法差不多，不過在講解 Dijkstra 算法框架之前，我們首先需要對之前的框架進(jìn)行如下改造：

想辦法去掉while循環(huán)里面的for循環(huán)。

為什么？有了剛才的鋪墊，這個不難理解，剛才說for循環(huán)是干什么用的來著？

是為了讓二叉樹一層一層往下遍歷，讓 BFS 算法一步一步向外擴(kuò)散，因?yàn)檫@個層數(shù)depth，或者這個步數(shù)step，在之前的場景中有用。

但現(xiàn)在我們想解決「加權(quán)圖」中的最短路徑問題，「步數(shù)」已經(jīng)沒有參考意義了，「路徑的權(quán)重之和」才有意義，所以這個for循環(huán)可以被去掉。

怎么去掉？就拿二叉樹的層級遍歷來說，其實(shí)你可以直接去掉for循環(huán)相關(guān)的代碼：

// 輸入一棵二叉樹的根節(jié)點(diǎn)，遍歷這棵二叉樹所有節(jié)點(diǎn)void levelTraverse（TreeNode root） {

if （root == null） return 0;

Queue《TreeNode》 q = new LinkedList《》（）;

q.offer（root）;

// 遍歷二叉樹的每一個節(jié)點(diǎn)

while （！q.isEmpty（）） {

TreeNode cur = q.poll（）;

printf（“我不知道節(jié)點(diǎn) %s 在第幾層”， cur）;

// 將子節(jié)點(diǎn)放入隊列

if （cur.left ！= null） {

q.offer（cur.left）;

}

if （cur.right ！= null） {

q.offer（cur.right）;

}

}

}

但問題是，沒有for循環(huán)，你也沒辦法維護(hù)depth變量了。

如果你想同時維護(hù)depth變量，讓每個節(jié)點(diǎn)cur知道自己在第幾層，可以想其他辦法，比如新建一個State類，記錄每個節(jié)點(diǎn)所在的層數(shù)：

class State {

// 記錄 node 節(jié)點(diǎn)的深度

int depth;

TreeNode node;

State（TreeNode node， int depth） {

this.depth = depth;

this.node = node;

}

}

// 輸入一棵二叉樹的根節(jié)點(diǎn)，遍歷這棵二叉樹所有節(jié)點(diǎn)void levelTraverse（TreeNode root） {

if （root == null） return 0;

Queue《State》 q = new LinkedList《》（）;

q.offer（new State（root， 1））;

// 遍歷二叉樹的每一個節(jié)點(diǎn)

while （！q.isEmpty（）） {

State cur = q.poll（）;

TreeNode cur_node = cur.node;

int cur_depth = cur.depth;

printf（“節(jié)點(diǎn) %s 在第 %s 層”， cur_node， cur_depth）;

// 將子節(jié)點(diǎn)放入隊列

if （cur_node.left ！= null） {

q.offer（new State（cur_node.left， cur_depth + 1））;

}

if （cur_node.right ！= null） {

q.offer（new State（cur_node.right， cur_depth + 1））;

}

}

}

這樣，我們就可以不使用for循環(huán)也確切地知道每個二叉樹節(jié)點(diǎn)的深度了。

如果你能夠理解上面這段代碼，我們就可以來看 Dijkstra 算法的代碼框架了。

Dijkstra 算法框架

首先，我們先看一下 Dijkstra 算法的簽名：

// 輸入一幅圖和一個起點(diǎn) start，計算 start 到其他節(jié)點(diǎn)的最短距離int［］ dijkstra（int start， List《Integer》［］ graph）;

輸入是一幅圖graph和一個起點(diǎn)start，返回是一個記錄最短路徑權(quán)重的數(shù)組。

比方說，輸入起點(diǎn)start = 3，函數(shù)返回一個int［］數(shù)組，假設(shè)賦值給distTo變量，那么從起點(diǎn)3到節(jié)點(diǎn)6的最短路徑權(quán)重的值就是distTo［6］。

是的，標(biāo)準(zhǔn)的 Dijkstra 算法會把從起點(diǎn)start到所有其他節(jié)點(diǎn)的最短路徑都算出來。

當(dāng)然，如果你的需求只是計算從起點(diǎn)start到某一個終點(diǎn)end的最短路徑，那么在標(biāo)準(zhǔn) Dijkstra 算法上稍作修改就可以更高效地完成這個需求，這個我們后面再說。

其次，我們也需要一個State類來輔助算法的運(yùn)行：

class State {

// 圖節(jié)點(diǎn)的 id

int id;

// 從 start 節(jié)點(diǎn)到當(dāng)前節(jié)點(diǎn)的距離

int distFromStart;

State（int id， int distFromStart） {

this.id = id;

this.distFromStart = distFromStart;

}

}

類似剛才二叉樹的層序遍歷，我們也需要用State類記錄一些額外信息，也就是使用distFromStart變量記錄從起點(diǎn)start到當(dāng)前這個節(jié)點(diǎn)的距離。

剛才說普通 BFS 算法中，根據(jù) BFS 的邏輯和無權(quán)圖的特點(diǎn)，第一次遇到某個節(jié)點(diǎn)所走的步數(shù)就是最短距離，所以用一個visited數(shù)組防止走回頭路，每個節(jié)點(diǎn)只會經(jīng)過一次。

加權(quán)圖中的 Dijkstra 算法和無權(quán)圖中的普通 BFS 算法不同，在 Dijkstra 算法中，你第一次經(jīng)過某個節(jié)點(diǎn)時的路徑權(quán)重，不見得就是最小的，所以對于同一個節(jié)點(diǎn)，我們可能會經(jīng)過多次，而且每次的distFromStart可能都不一樣，比如下圖：

我會經(jīng)過節(jié)點(diǎn)5三次，每次的distFromStart值都不一樣，那我取distFromStart最小的那次，不就是從起點(diǎn)start到節(jié)點(diǎn)5的最短路徑權(quán)重了么？

好了，明白上面的幾點(diǎn)，我們可以來看看 Dijkstra 算法的代碼模板。

其實(shí)，Dijkstra 可以理解成一個帶 dp table（或者說備忘錄）的 BFS 算法，偽碼如下：

// 返回節(jié)點(diǎn) from 到節(jié)點(diǎn) to 之間的邊的權(quán)重int weight（int from， int to）;

// 輸入節(jié)點(diǎn) s 返回 s 的相鄰節(jié)點(diǎn)List《Integer》 adj（int s）;

// 輸入一幅圖和一個起點(diǎn) start，計算 start 到其他節(jié)點(diǎn)的最短距離int［］ dijkstra（int start， List《Integer》［］ graph） {

// 圖中節(jié)點(diǎn)的個數(shù)

int V = graph.length;

// 記錄最短路徑的權(quán)重，你可以理解為 dp table

// 定義：distTo［i］ 的值就是節(jié)點(diǎn) start 到達(dá)節(jié)點(diǎn) i 的最短路徑權(quán)重

int［］ distTo = new int［V］;

// 求最小值，所以 dp table 初始化為正無窮

Arrays.fill（distTo， Integer.MAX_VALUE）;

// base case，start 到 start 的最短距離就是 0

distTo［start］ = 0;

// 優(yōu)先級隊列，distFromStart 較小的排在前面

Queue《State》 pq = new PriorityQueue《》（（a， b） -》 {

return a.distFromStart - b.distFromStart;

}）;

// 從起點(diǎn) start 開始進(jìn)行 BFS

pq.offer（new State（start， 0））;

while （！pq.isEmpty（）） {

State curState = pq.poll（）;

int curNodeID = curState.id;

int curDistFromStart = curState.distFromStart;

if （curDistFromStart 》 distTo［curNodeID］） {

// 已經(jīng)有一條更短的路徑到達(dá) curNode 節(jié)點(diǎn)了

continue;

}

// 將 curNode 的相鄰節(jié)點(diǎn)裝入隊列

for （int nextNodeID ： adj（curNodeID）） {

// 看看從 curNode 達(dá)到 nextNode 的距離是否會更短

int distToNextNode = distTo［curNodeID］ + weight（curNodeID， nextNodeID）;

if （distTo［nextNodeID］ 》 distToNextNode） {

// 更新 dp table

distTo［nextNodeID］ = distToNextNode;

// 將這個節(jié)點(diǎn)以及距離放入隊列

pq.offer（new State（nextNodeID， distToNextNode））;

}

}

}

return distTo;

}

對比普通的 BFS 算法，你可能會有以下疑問：

1、沒有visited集合記錄已訪問的節(jié)點(diǎn)，所以一個節(jié)點(diǎn)會被訪問多次，會被多次加入隊列，那會不會導(dǎo)致隊列永遠(yuǎn)不為空，造成死循環(huán)？

2、為什么用優(yōu)先級隊列PriorityQueue而不是LinkedList實(shí)現(xiàn)的普通隊列？為什么要按照distFromStart的值來排序？

3、如果我只想計算起點(diǎn)start到某一個終點(diǎn)end的最短路徑，是否可以修改算法，提升一些效率？

我們先回答第一個問題，為什么這個算法不用visited集合也不會死循環(huán)。

對于這類問題，我教你一個思考方法：

循環(huán)結(jié)束的條件是隊列為空，那么你就要注意看什么時候往隊列里放元素（調(diào)用offer）方法，再注意看什么時候從隊列往外拿元素（調(diào)用poll方法）。

while循環(huán)每執(zhí)行一次，都會往外拿一個元素，但想往隊列里放元素，可就有很多限制了，必須滿足下面這個條件：

// 看看從 curNode 達(dá)到 nextNode 的距離是否會更短if （distTo［nextNodeID］ 》 distToNextNode） {

// 更新 dp table

distTo［nextNodeID］ = distToNextNode;

pq.offer（new State（nextNodeID， distToNextNode））;

}

這也是為什么我說distTo數(shù)組可以理解成我們熟悉的 dp table，因?yàn)檫@個算法邏輯就是在不斷的最小化distTo數(shù)組中的元素：

如果你能讓到達(dá)nextNodeID的距離更短，那就更新distTo［nextNodeID］的值，讓你入隊，否則的話對不起，不讓入隊。

因?yàn)閮蓚€節(jié)點(diǎn)之間的最短距離（路徑權(quán)重）肯定是一個確定的值，不可能無限減小下去，所以隊列一定會空，隊列空了之后，distTo數(shù)組中記錄的就是從start到其他節(jié)點(diǎn)的最短距離。

接下來解答第二個問題，為什么要用PriorityQueue而不是LinkedList實(shí)現(xiàn)的普通隊列？

如果你非要用普通隊列，其實(shí)也沒問題的，你可以直接把PriorityQueue改成LinkedList，也能得到正確答案，但是效率會低很多。

Dijkstra 算法使用優(yōu)先級隊列，主要是為了效率上的優(yōu)化，類似一種貪心算法的思路。

為什么說是一種貪心思路呢，比如說下面這種情況，你想計算從起點(diǎn)start到終點(diǎn)end的最短路徑權(quán)重：

你下一步想遍歷那個節(jié)點(diǎn)？就當(dāng)前的情況來看，你覺得哪條路徑更有「潛力」成為最短路徑中的一部分？

從目前的情況來看，顯然橙色路徑的可能性更大嘛，所以我們希望節(jié)點(diǎn)2排在隊列靠前的位置，優(yōu)先被拿出來向后遍歷。

所以我們使用PriorityQueue作為隊列，讓distFromStart的值較小的節(jié)點(diǎn)排在前面，這就類似我們之前講 貪心算法 說到的貪心思路，可以很大程度上優(yōu)化算法的效率。

大家應(yīng)該聽過 Bellman-Ford 算法，這個算法是一種更通用的最短路徑算法，因?yàn)樗梢蕴幚韼в胸?fù)權(quán)重邊的圖，Bellman-Ford 算法邏輯和 Dijkstra 算法非常類似，用到的就是普通隊列，本文就提一句，后面有空再具體寫。

接下來說第三個問題，如果只關(guān)心起點(diǎn)start到某一個終點(diǎn)end的最短路徑，是否可以修改代碼提升算法效率。

肯定可以的，因?yàn)槲覀儤?biāo)準(zhǔn) Dijkstra 算法會算出start到所有其他節(jié)點(diǎn)的最短路徑，你只想計算到end的最短路徑，相當(dāng)于減少計算量，當(dāng)然可以提升效率。

需要在代碼中做的修改也非常少，只要改改函數(shù)簽名，再加個 if 判斷就行了：

// 輸入起點(diǎn) start 和終點(diǎn) end，計算起點(diǎn)到終點(diǎn)的最短距離int dijkstra（int start， int end， List《Integer》［］ graph） {

// 。..

while （！pq.isEmpty（）） {

State curState = pq.poll（）;

int curNodeID = curState.id;

int curDistFromStart = curState.distFromStart;

// 在這里加一個判斷就行了，其他代碼不用改

if （curNodeID == end） {

return curDistFromStart;

}

if （curDistFromStart 》 distTo［curNodeID］） {

continue;

}

// 。..

}

// 如果運(yùn)行到這里，說明從 start 無法走到 end

return Integer.MAX_VALUE;

}

因?yàn)閮?yōu)先級隊列自動排序的性質(zhì)，每次從隊列里面拿出來的都是distFromStart值最小的，所以當(dāng)你從隊頭拿出一個節(jié)點(diǎn)，如果發(fā)現(xiàn)這個節(jié)點(diǎn)就是終點(diǎn)end，那么distFromStart對應(yīng)的值就是從start到end的最短距離。

這個算法較之前的實(shí)現(xiàn)提前 return 了，所以效率有一定的提高。

時間復(fù)雜度分析

Dijkstra 算法的時間復(fù)雜度是多少？你去網(wǎng)上查，可能會告訴你是O（ElogV），其中E代表圖中邊的條數(shù)，V代表圖中節(jié)點(diǎn)的個數(shù)。

因?yàn)槔硐肭闆r下優(yōu)先級隊列中最多裝V個節(jié)點(diǎn)，對優(yōu)先級隊列的操作次數(shù)和E成正比，所以整體的時間復(fù)雜度就是O（ElogV）。

不過這是理想情況，Dijkstra 算法的代碼實(shí)現(xiàn)有很多版本，不同編程語言或者不同數(shù)據(jù)結(jié)構(gòu) API 都會導(dǎo)致算法的時間復(fù)雜度發(fā)生一些改變。

比如本文實(shí)現(xiàn)的 Dijkstra 算法，使用了 Java 的PriorityQueue這個數(shù)據(jù)結(jié)構(gòu)，這個容器類底層使用二叉堆實(shí)現(xiàn)，但沒有提供通過索引操作隊列中元素的 API，所以隊列中會有重復(fù)的節(jié)點(diǎn)，最多可能有E個節(jié)點(diǎn)存在隊列中。

所以本文實(shí)現(xiàn)的 Dijkstra 算法復(fù)雜度并不是理想情況下的O（ElogV），而是O（ElogE），可能會略大一些，因?yàn)閳D中邊的條數(shù)一般是大于節(jié)點(diǎn)的個數(shù)的。

不過就對數(shù)函數(shù)來說，就算真數(shù)大一些，對數(shù)函數(shù)的結(jié)果也大不了多少，所以這個算法實(shí)現(xiàn)的實(shí)際運(yùn)行效率也是很高的，以上只是理論層面的時間復(fù)雜度分析，供大家參考。

秒殺三道題目

以上說了 Dijkstra 算法的框架，下面我們套用這個框架做幾道題，實(shí)踐出真知。

第一題是力扣第 743 題「網(wǎng)絡(luò)延遲時間」，題目如下：

函數(shù)簽名如下：

// times 記錄邊和權(quán)重，n 為節(jié)點(diǎn)個數(shù)（從 1 開始），k 為起點(diǎn)// 計算從 k 發(fā)出的信號至少需要多久傳遍整幅圖int networkDelayTime（int［］［］ times， int n， int k）

讓你求所有節(jié)點(diǎn)都收到信號的時間，你把所謂的傳遞時間看做距離，實(shí)際上就是問你「從節(jié)點(diǎn)k到其他所有節(jié)點(diǎn)的最短路徑中，最長的那條最短路徑距離是多少」，說白了就是讓你算從節(jié)點(diǎn)k出發(fā)到其他所有節(jié)點(diǎn)的最短路徑，就是標(biāo)準(zhǔn)的 Dijkstra 算法。

在用 Dijkstra 之前，別忘了要滿足一些條件，加權(quán)有向圖，沒有負(fù)權(quán)重邊，OK，可以用 Dijkstra 算法計算最短路徑。

根據(jù)我們之前 Dijkstra 算法的框架，我們可以寫出下面代碼：

public int networkDelayTime（int［］［］ times， int n， int k） {

// 節(jié)點(diǎn)編號是從 1 開始的，所以要一個大小為 n + 1 的鄰接表

List《int［］》［］ graph = new LinkedList［n + 1］;

for （int i = 1; i 《= n; i++） {

graph［i］ = new LinkedList《》（）;

}

// 構(gòu)造圖

for （int［］ edge ： times） {

int from = edge［0］;

int to = edge［1］;

int weight = edge［2］;

// from -》 List《（to， weight）》

// 鄰接表存儲圖結(jié)構(gòu)，同時存儲權(quán)重信息

graph［from］.add（new int［］{to， weight}）;

}

// 啟動 dijkstra 算法計算以節(jié)點(diǎn) k 為起點(diǎn)到其他節(jié)點(diǎn)的最短路徑

int［］ distTo = dijkstra（k， graph）;

// 找到最長的那一條最短路徑

int res = 0;

for （int i = 1; i 《 distTo.length; i++） {

if （distTo［i］ == Integer.MAX_VALUE） {

// 有節(jié)點(diǎn)不可達(dá)，返回 -1

return -1;

}

res = Math.max（res， distTo［i］）;

}

return res;

}

// 輸入一個起點(diǎn) start，計算從 start 到其他節(jié)點(diǎn)的最短距離int［］ dijkstra（int start， List《int［］》［］ graph） {}

上述代碼首先利用題目輸入的數(shù)據(jù)轉(zhuǎn)化成鄰接表表示一幅圖，接下來我們可以直接套用 Dijkstra 算法的框架：

class State {

// 圖節(jié)點(diǎn)的 id

int id;

// 從 start 節(jié)點(diǎn)到當(dāng)前節(jié)點(diǎn)的距離

int distFromStart;

State（int id， int distFromStart） {

this.id = id;

this.distFromStart = distFromStart;

}

}

// 輸入一個起點(diǎn) start，計算從 start 到其他節(jié)點(diǎn)的最短距離int［］ dijkstra（int start， List《int［］》［］ graph） {

// 定義：distTo［i］ 的值就是起點(diǎn) start 到達(dá)節(jié)點(diǎn) i 的最短路徑權(quán)重

int［］ distTo = new int［graph.length］;

Arrays.fill（distTo， Integer.MAX_VALUE）;

// base case，start 到 start 的最短距離就是 0

distTo［start］ = 0;

// 優(yōu)先級隊列，distFromStart 較小的排在前面

Queue《State》 pq = new PriorityQueue《》（（a， b） -》 {

return a.distFromStart - b.distFromStart;

}）;

// 從起點(diǎn) start 開始進(jìn)行 BFS

pq.offer（new State（start， 0））;

while （！pq.isEmpty（）） {

State curState = pq.poll（）;

int curNodeID = curState.id;

int curDistFromStart = curState.distFromStart;

if （curDistFromStart 》 distTo［curNodeID］） {

continue;

}

// 將 curNode 的相鄰節(jié)點(diǎn)裝入隊列

for （int［］ neighbor ： graph［curNodeID］） {

int nextNodeID = neighbor［0］;

int distToNextNode = distTo［curNodeID］ + neighbor［1］;

// 更新 dp table

if （distTo［nextNodeID］ 》 distToNextNode） {

distTo［nextNodeID］ = distToNextNode;

pq.offer（new State（nextNodeID， distToNextNode））;

}

}

}

return distTo;

}

你對比之前說的代碼框架，只要稍稍修改，就可以把這道題目解決了。

感覺這道題完全沒有難度，下面我們再看一道題目，力扣第 1631 題「最小體力消耗路徑」：

函數(shù)簽名如下：

// 輸入一個二維矩陣，計算從左上角到右下角的最小體力消耗int minimumEffortPath（int［］［］ heights）;

我們常見的二維矩陣題目，如果讓你從左上角走到右下角，比較簡單的題一般都會限制你只能向右或向下走，但這道題可沒有限制哦，你可以上下左右隨便走，只要路徑的「體力消耗」最小就行。

如果你把二維數(shù)組中每個（x， y）坐標(biāo)看做一個節(jié)點(diǎn)，它的上下左右坐標(biāo)就是相鄰節(jié)點(diǎn)，它對應(yīng)的值和相鄰坐標(biāo)對應(yīng)的值之差的絕對值就是題目說的「體力消耗」，你就可以理解為邊的權(quán)重。

這樣一想，是不是就在讓你以左上角坐標(biāo)為起點(diǎn)，以右下角坐標(biāo)為終點(diǎn)，計算起點(diǎn)到終點(diǎn)的最短路徑？Dijkstra 算法是不是可以做到？

// 輸入起點(diǎn) start 和終點(diǎn) end，計算起點(diǎn)到終點(diǎn)的最短距離int dijkstra（int start， int end， List《Integer》［］ graph）

只不過，這道題中評判一條路徑是長還是短的標(biāo)準(zhǔn)不再是路徑經(jīng)過的權(quán)重總和，而是路徑經(jīng)過的權(quán)重最大值。

明白這一點(diǎn)，再想一下使用 Dijkstra 算法的前提，加權(quán)有向圖，沒有負(fù)權(quán)重邊，求最短路徑，OK，可以使用，咱們來套框架。

二維矩陣抽象成圖，我們先實(shí)現(xiàn)一下圖的adj方法，之后的主要邏輯會清晰一些：

// 方向數(shù)組，上下左右的坐標(biāo)偏移量int［］［］ dirs = new int［］［］{{0，1}， {1，0}， {0，-1}， {-1，0}};

// 返回坐標(biāo) （x， y） 的上下左右相鄰坐標(biāo)

List《int［］》 adj（int［］［］ matrix， int x， int y） {

int m = matrix.length， n = matrix［0］.length;

// 存儲相鄰節(jié)點(diǎn)

List《int［］》 neighbors = new ArrayList《》（）;

for （int［］ dir ： dirs） {

int nx = x + dir［0］;

int ny = y + dir［1］;

if （nx 》= m || nx 《 0 || ny 》= n || ny 《 0） {

// 索引越界

continue;

}

neighbors.add（new int［］{nx， ny}）;

}

return neighbors;

}

類似的，我們現(xiàn)在認(rèn)為一個二維坐標(biāo)（x， y）是圖中的一個節(jié)點(diǎn)，所以這個State類也需要修改一下：

class State {

// 矩陣中的一個位置

int x， y;

// 從起點(diǎn) （0， 0） 到當(dāng)前位置的最小體力消耗（距離）

int effortFromStart;

State（int x， int y， int effortFromStart） {

this.x = x;

this.y = y;

this.effortFromStart = effortFromStart;

}

}

接下來，就可以套用 Dijkstra 算法的代碼模板了：

// Dijkstra 算法，計算 （0， 0） 到 （m - 1， n - 1） 的最小體力消耗int minimumEffortPath（int［］［］ heights） {

int m = heights.length， n = heights［0］.length;

// 定義：從 （0， 0） 到 （i， j） 的最小體力消耗是 effortTo［i］［j］

int［］［］ effortTo = new int［m］［n］;

// dp table 初始化為正無窮

for （int i = 0; i 《 m; i++） {

Arrays.fill（effortTo［i］， Integer.MAX_VALUE）;

}

// base case，起點(diǎn)到起點(diǎn)的最小消耗就是 0

effortTo［0］［0］ = 0;

// 優(yōu)先級隊列，effortFromStart 較小的排在前面

Queue《State》 pq = new PriorityQueue《》（（a， b） -》 {

return a.effortFromStart - b.effortFromStart;

}）;

// 從起點(diǎn) （0， 0） 開始進(jìn)行 BFS

pq.offer（new State（0， 0， 0））;

while （！pq.isEmpty（）） {

State curState = pq.poll（）;

int curX = curState.x;

int curY = curState.y;

int curEffortFromStart = curState.effortFromStart;

// 到達(dá)終點(diǎn)提前結(jié)束

if （curX == m - 1 && curY == n - 1） {

return curEffortFromStart;

}

if （curEffortFromStart 》 effortTo［curX］［curY］） {

continue;

}

// 將 （curX， curY） 的相鄰坐標(biāo)裝入隊列

for （int［］ neighbor ： adj（heights， curX， curY）） {

int nextX = neighbor［0］;

int nextY = neighbor［1］;

// 計算從 （curX， curY） 達(dá)到 （nextX， nextY） 的消耗

int effortToNextNode = Math.max（

effortTo［curX］［curY］，

Math.abs（heights［curX］［curY］ - heights［nextX］［nextY］）

）;

// 更新 dp table

if （effortTo［nextX］［nextY］ 》 effortToNextNode） {

effortTo［nextX］［nextY］ = effortToNextNode;

pq.offer（new State（nextX， nextY， effortToNextNode））;

}

}

}

// 正常情況不會達(dá)到這個 return

return -1;

}

你看，稍微改一改代碼模板，這道題就解決了。

最后看一道題吧，力扣第 1514 題「概率最大的路徑」，看下題目：

函數(shù)簽名如下：

// 輸入一幅無向圖，邊上的權(quán)重代表概率，返回從 start 到達(dá) end 最大的概率double maxProbability（int n， int［］［］ edges， double［］ succProb， int start， int end）

我說這題一看就是 Dijkstra 算法，但聰明的你肯定會反駁我：

1、這題給的是無向圖，也可以用 Dijkstra 算法嗎？

2、更重要的是，Dijkstra 算法計算的是最短路徑，計算的是最小值，這題讓你計算最大概率是一個最大值，怎么可能用 Dijkstra 算法呢？

問得好！

首先關(guān)于有向圖和無向圖，前文 圖算法基礎(chǔ) 說過，無向圖本質(zhì)上可以認(rèn)為是「雙向圖」，從而轉(zhuǎn)化成有向圖。

重點(diǎn)說說最大值和最小值這個問題，其實(shí) Dijkstra 和很多最優(yōu)化算法一樣，計算的是「最優(yōu)值」，這個最優(yōu)值可能是最大值，也可能是最小值。

標(biāo)準(zhǔn) Dijkstra 算法是計算最短路徑的，但你有想過為什么 Dijkstra 算法不允許存在負(fù)權(quán)重邊么？

因?yàn)?Dijkstra 計算最短路徑的正確性依賴一個前提：路徑中每增加一條邊，路徑的總權(quán)重就會增加。

這個前提的數(shù)學(xué)證明大家有興趣可以自己搜索一下，我這里只說結(jié)論，其實(shí)你把這個結(jié)論反過來也是 OK 的：

如果你想計算最長路徑，路徑中每增加一條邊，路徑的總權(quán)重就會減少，要是能夠滿足這個條件，也可以用 Dijkstra 算法。

你看這道題是不是符合這個條件？邊和邊之間是乘法關(guān)系，每條邊的概率都是小于 1 的，所以肯定會越乘越小。

只不過，這道題的解法要把優(yōu)先級隊列的排序順序反過來，一些 if 大小判斷也要反過來，我們直接看解法代碼吧：

double maxProbability（int n， int［］［］ edges， double［］ succProb， int start， int end） {

List《double［］》［］ graph = new LinkedList［n］;

for （int i = 0; i 《 n; i++） {

graph［i］ = new LinkedList《》（）;

}

// 構(gòu)造鄰接表結(jié)構(gòu)表示圖

for （int i = 0; i 《 edges.length; i++） {

int from = edges［i］［0］;

int to = edges［i］［1］;

double weight = succProb［i］;

// 無向圖就是雙向圖；先把 int 統(tǒng)一轉(zhuǎn)成 double，待會再轉(zhuǎn)回來

graph［from］.add（new double［］{（double）to， weight}）;

graph［to］.add（new double［］{（double）from， weight}）;

}

return dijkstra（start， end， graph）;

}

class State {

// 圖節(jié)點(diǎn)的 id

int id;

// 從 start 節(jié)點(diǎn)到達(dá)當(dāng)前節(jié)點(diǎn)的概率

double probFromStart;

State（int id， double probFromStart） {

this.id = id;

this.probFromStart = probFromStart;

}

}

double dijkstra（int start， int end， List《double［］》［］ graph） {

// 定義：probTo［i］ 的值就是節(jié)點(diǎn) start 到達(dá)節(jié)點(diǎn) i 的最大概率

double［］ probTo = new double［graph.length］;

// dp table 初始化為一個取不到的最小值

Arrays.fill（probTo， -1）;

// base case，start 到 start 的概率就是 1

probTo［start］ = 1;

// 優(yōu)先級隊列，probFromStart 較大的排在前面

Queue《State》 pq = new PriorityQueue《》（（a， b） -》 {

return Double.compare（b.probFromStart， a.probFromStart）;

}）;

// 從起點(diǎn) start 開始進(jìn)行 BFS

pq.offer（new State（start， 1））;

while （！pq.isEmpty（）） {

State curState = pq.poll（）;

int curNodeID = curState.id;

double curProbFromStart = curState.probFromStart;

// 遇到終點(diǎn)提前返回

if （curNodeID == end） {

return curProbFromStart;

}

if （curProbFromStart 《 probTo［curNodeID］） {

// 已經(jīng)有一條概率更大的路徑到達(dá) curNode 節(jié)點(diǎn)了

continue;

}

// 將 curNode 的相鄰節(jié)點(diǎn)裝入隊列

for （double［］ neighbor ： graph［curNodeID］） {

int nextNodeID = （int）neighbor［0］;

// 看看從 curNode 達(dá)到 nextNode 的概率是否會更大

double probToNextNode = probTo［curNodeID］ * neighbor［1］;

if （probTo［nextNodeID］ 《 probToNextNode） {

probTo［nextNodeID］ = probToNextNode;

pq.offer（new State（nextNodeID， probToNextNode））;

}

}

}

// 如果到達(dá)這里，說明從 start 開始無法到達(dá) end，返回 0

return 0.0;

}

好了，到這里本文就結(jié)束了，總共 6000 多字，這三道例題都是比較困難的，如果你能夠看到這里，真得給你鼓掌。

還是那句話，做題在質(zhì)不在量，希望大家能夠透徹理解最基本的數(shù)據(jù)結(jié)構(gòu)，以不變應(yīng)萬變。

責(zé)任編輯：haq