一、引言
有限元法是求解復(fù)雜工程問(wèn)題的一種近似數(shù)值解法,現(xiàn)已廣泛應(yīng)用到力學(xué)、熱學(xué)、電磁學(xué)等各個(gè)學(xué)科,主要分析工作環(huán)境下物體的線性和非線性靜動(dòng)態(tài)特性等性能。
有限元法求解問(wèn)題的基本過(guò)程主要包括:分析對(duì)象的離散化,有限元求解和計(jì)算結(jié)果的處理三部分。
曾經(jīng)有人做過(guò)統(tǒng)計(jì):三個(gè)階段所用的時(shí)間分別占總時(shí)間的40%~50%、5%及50%~55%。也就是說(shuō),當(dāng)利用有限元分析對(duì)象時(shí),主要時(shí)間是用于對(duì)象的離散及結(jié)果的處理。如果采用人工方法離散對(duì)象和處理計(jì)算結(jié)果,勢(shì)必費(fèi)力、費(fèi)時(shí)且極易出錯(cuò),尤其當(dāng)分析模型復(fù)雜時(shí),采用人工方法甚至很難進(jìn)行,這將嚴(yán)重影響高級(jí)有限元分析程序的推廣和使用。因此,開(kāi)展自動(dòng)離散對(duì)象及結(jié)果的計(jì)算機(jī)可視化顯示的研究是一項(xiàng)重要而緊迫的任務(wù)。
可喜的是,隨著計(jì)算機(jī)及計(jì)算技術(shù)的飛速發(fā)展,出現(xiàn)了開(kāi)發(fā)對(duì)象的自動(dòng)離散及有限元分析結(jié)果的計(jì)算機(jī)可視化顯示的熱潮,使有限元分析的“瓶頸”現(xiàn)象得以逐步解決,對(duì)象的離散從手工到半自動(dòng)到全自動(dòng),從簡(jiǎn)單對(duì)象的單維單一網(wǎng)格到復(fù)雜對(duì)象的多維多種網(wǎng)格單元,從單材料到多種材料,從單純的離散到自適應(yīng)離散,從對(duì)象的性能校核到自動(dòng)自適應(yīng)動(dòng)態(tài)設(shè)計(jì)、分析,這些重大發(fā)展使有限元分析擺脫了僅為性能校核工具的原始階段,計(jì)算結(jié)果的計(jì)算機(jī)可視化顯示從簡(jiǎn)單的應(yīng)力、位移和溫度等場(chǎng)的靜動(dòng)態(tài)顯示、彩色調(diào)色顯示,一躍成為對(duì)受載對(duì)象可能出現(xiàn)缺陷(裂紋等)的位置、形狀、大小及其可能波及區(qū)域的顯示等,這種從抽象數(shù)據(jù)到計(jì)算機(jī)形象化顯示的飛躍是現(xiàn)在甚至將來(lái)計(jì)算機(jī)集成設(shè)計(jì)、分析的重要組成部分。
二、有限元分析對(duì)網(wǎng)格剖分的要求
有限元網(wǎng)格生成就是將工作環(huán)境下的物體離散成簡(jiǎn)單單元的過(guò)程,常用的簡(jiǎn)單單元包括:一維桿元及集中質(zhì)量元、二維三角形、四邊形元和三維四面體元、五面體元和六面體元。他們的邊界形狀主要有直線型、曲線型和曲面型。對(duì)于邊界為曲線(面)型的單元,有限元分析要求各邊或面上有若干點(diǎn),這樣,既可保證單元的形狀,又可提高求解精度、準(zhǔn)確性及加快收斂速度。不同維數(shù)的同一物體可以剖分為由多種單元混合而成的網(wǎng)格。網(wǎng)格剖分應(yīng)滿足以下要求:
合法性。一個(gè)單元的結(jié)點(diǎn)不能落入其他單元內(nèi)部,在單元邊界上的結(jié)點(diǎn)均應(yīng)作為單元的結(jié)點(diǎn),不可丟棄。
相容性。單元必須落在待分區(qū)域內(nèi)部,不能落入外部,且單元并集等于待分區(qū)域。
逼近精確性。待分區(qū)域的頂點(diǎn)(包括特殊點(diǎn))必須是單元的結(jié)點(diǎn),待分區(qū)域的邊界(包括特殊邊及面)被單元邊界所逼近。
良好的單元形狀。單元最佳形狀是正多邊形或正多面體。
良好的剖分過(guò)渡性。單元之間過(guò)渡應(yīng)相對(duì)平穩(wěn),否則,將影響計(jì)算結(jié)果的準(zhǔn)確性甚至使有限元計(jì)算無(wú)法計(jì)算下去。
三、現(xiàn)有有限元網(wǎng)格剖分方法
K. Ho-Le 對(duì)網(wǎng)格生成算法進(jìn)行了系統(tǒng)分類(lèi),該分類(lèi)方法可沿用至今,它們是拓?fù)浞纸夥ā⒔Y(jié)點(diǎn)連元法、網(wǎng)格模板法、映射法和幾何分解法五種。目前,主要是上述方法的混合使用及現(xiàn)代技術(shù)的綜合應(yīng)用。
1. 映射法
映射法是一種半自動(dòng)網(wǎng)格生成方法,根據(jù)映射函數(shù)的不同,主要可分為超限映射和等參映射。因前一種映射在幾何逼近精度上比后一種高,故被廣泛采用。
映射法的基本思想是:在簡(jiǎn)單區(qū)域內(nèi)采用某種映射函數(shù)構(gòu)造簡(jiǎn)單區(qū)域的邊界點(diǎn)和內(nèi)點(diǎn),并按某種規(guī)則連接結(jié)點(diǎn)構(gòu)成網(wǎng)格單元。這種方法可以很方便地生成四邊形和六面體單元,若需要,也很容易轉(zhuǎn)換成三角形和四面體單元。
該法的主要缺點(diǎn):首先必須將待分區(qū)域子劃分為所要求的簡(jiǎn)單區(qū)域,這是一個(gè)十分復(fù)雜且很難實(shí)現(xiàn)自動(dòng)化的過(guò)程。對(duì)復(fù)雜域采用手工方法劃分甚至不可能,通常各簡(jiǎn)單區(qū)域邊界采用等份劃分。另外,該法在控制單元形狀及網(wǎng)格密度方面是困難的。鑒于簡(jiǎn)單區(qū)域自動(dòng)劃分的困難性,Blacker試圖采用知識(shí)系統(tǒng)和聯(lián)合體素方法解決,但在復(fù)雜多孔域上仍難以處理,主要是體素?cái)?shù)量和形狀有限,將待分區(qū)域全自動(dòng)劃分為有限的預(yù)定體素并集是很難完全實(shí)現(xiàn)的。
2. 拓?fù)浞纸夥?/p>
在不考慮網(wǎng)格單元大小和形狀情況下,Wordenweber提出了使用三種算子連接多邊形各頂點(diǎn)形成粗三角形的二維拓?fù)浞纸夥ǎ缓蠹?xì)化粗單元至預(yù)定規(guī)定的網(wǎng)格密度為止。三種算子使用順序?yàn)椋簅pj、opl、op0 。同時(shí),Wordenweber也提出了在三維域使用opj(i=0,1,2,3) 和opp五種算子剖分實(shí)體。Woo、Thomasma和Saxena等擴(kuò)充了該法,并將其有效地應(yīng)用到多面體實(shí)體有限元自動(dòng)網(wǎng)格生成中。Saxena稱(chēng)該法為EE法,并已與RSD法混合使用構(gòu)成RSD/EE法。單一的拓?fù)浞纸夥ㄒ蛑灰蕾囉趲缀误w的拓?fù)浣Y(jié)構(gòu)使網(wǎng)格剖分不理想,有時(shí)甚至很差。
3. 幾何分解法
凡在產(chǎn)生結(jié)點(diǎn)的同時(shí)也確定結(jié)點(diǎn)間連接關(guān)系的方法均稱(chēng)為幾何分解法,常用的有兩種:遞歸法和迭代法。
遞歸法:Tracy、左建政和Chae等先離散二維物體邊界,然后沿離散邊界向物體內(nèi)挖掉一個(gè)、兩個(gè)或三個(gè)三角形,重復(fù)此操作直到區(qū)域挖空為止。Lindhom、Blacker和B.P. Johnston等使用的迭代法不同于前者,首先從物體中挖掉邊界層而不是單元,然后三角化邊界層。上述為二維迭代法,Chae在此基礎(chǔ)上發(fā)展了三維迭代幾何分解法,主要分兩步:采用二維迭代幾何分解法生成表面三角形,然后采用三種算子挖切凸體為四面體。在挖切時(shí),突出的特點(diǎn)在于采用新方法生成關(guān)鍵點(diǎn)。關(guān)鍵點(diǎn)的生成分兩步考慮:一是考慮新點(diǎn)對(duì)周?chē)婧瓦叺挠绊懀峭ㄟ^(guò)調(diào)整比例因子來(lái)確定新點(diǎn)位置。Chae也將所提出的算法成功地應(yīng)用于自適應(yīng)網(wǎng)格生成中,但由于被剖分物體形狀必須是單連通凸域,因此,不能實(shí)現(xiàn)全自動(dòng)網(wǎng)格生成。
迭代法:Bykat采用該法。他首先將物體劃分為凸體(手工或自動(dòng)),隨后根據(jù)網(wǎng)格密度分布,在每個(gè)凸體邊界上插入結(jié)點(diǎn),然后將物體中間“最長(zhǎng)軸”一分為二,在該軸上插入結(jié)點(diǎn),繼續(xù)對(duì)兩部分做遞歸分割直到最后子域均為三角形為止。商業(yè)網(wǎng)格生成軟件Triquamesh仍采用該法,只是分割線的選取與Bykat不同。幾何分解法的最大優(yōu)點(diǎn)是在離散物體時(shí)考慮網(wǎng)格單元的形狀和大小,因此,所生成的網(wǎng)格單元形狀和分布均較好。最大缺點(diǎn)是自動(dòng)化程度低,不利于復(fù)雜件網(wǎng)格生成。
4. 網(wǎng)格模板法(RSD法)
Shephard、Perucchio、Saxena、Sapidis和Yerry等,是這種方法成功運(yùn)用的主要代表。網(wǎng)格模板法生成有限元網(wǎng)格主要分兩步(以介紹三維實(shí)體為主):
第一,將待分實(shí)體用適當(dāng)大小的立方體箱(樹(shù)根)完全包容,按“一化八”原則遞歸離散,然后對(duì)每個(gè)八分塊按如下方法進(jìn)行分類(lèi):Procedure ModClassCell(Cell,S)=(‘IN’,‘OUT’,‘NIO’) If (八分塊中至少有一個(gè)頂點(diǎn)為‘OUT’且至少有一個(gè)頂點(diǎn)為‘IN’) then ‘NIO’ Else if (Cell (*S=() then ‘OUT’ Else if (Cell (*S=Cell) the ‘IN’ Else ‘NIO’ End; {procedure} 對(duì)于IN的八分塊繼續(xù)遞歸離散直到預(yù)定水平級(jí)為止,OUT的八分塊不再劃分,NIO的八分塊進(jìn)一步子劃分,且分類(lèi)直到預(yù)定水平級(jí)為止。稱(chēng)終了IN和NIO八分塊的并集為RSD模型。
第二,對(duì)已經(jīng)形成的RSD模型,目前已有多種生成網(wǎng)格的處理方法,主要有RSD/GDT法、RSD/EE法和RSD/DDT法。它們主要有以下特點(diǎn):
RSD/EE法不能處理曲面實(shí)體、非流形體和不連通實(shí)體。與此相反,RSD/DDT法卻能處理有孔的任意曲面實(shí)體、非流形體和不連通實(shí)體,而且所形成四面體形狀質(zhì)量良好。
RSD/DDT法根據(jù)需要以滿足條件為準(zhǔn)則插入新點(diǎn),因此所插入的新點(diǎn)數(shù)量少,而RSD/GDT法則會(huì)插入許多冗余點(diǎn)。
RSD/GDT法使用點(diǎn)/實(shí)體分類(lèi),使時(shí)間復(fù)雜性至少大一個(gè)數(shù)量級(jí),而RSD/DDT法不使用點(diǎn)/實(shí)體分類(lèi),因此,RSD/DDT法平均時(shí)間復(fù)雜性為O(N2),N為實(shí)體S的總表面數(shù)。RSD/EE法具有不確定的時(shí)間復(fù)雜性。
RSD/DDT法完全建立網(wǎng)格圖素拓?fù)湟灰粚?duì)應(yīng),因此拓?fù)涫墙∪模c此相反,RSD/GDT法是拓?fù)洳唤∪摹8鞣NRSD法的優(yōu)點(diǎn)是網(wǎng)格生成完全自動(dòng),網(wǎng)格剖分速度快,非常適用于自適應(yīng)網(wǎng)格生成。主要缺點(diǎn)是邊界單元形狀難于完全保證。另外,RSD法對(duì)物體的方向特別敏感。
5. 結(jié)點(diǎn)連元法
結(jié)點(diǎn)連元法是先生成結(jié)點(diǎn),然后連接結(jié)點(diǎn)構(gòu)成單元。最常用的是DT法和AFM法。
DT法的基本原理:任意給定N個(gè)平面點(diǎn)Pi(i=1,2,…,N) 構(gòu)成的點(diǎn)集為S,稱(chēng)滿足下列條件的點(diǎn)集Vi 為Voronoi多邊形。其中,Vi 滿足下列條件:Vi={ X:|X- Pi|(|X- Pj|,X(R2,i(j,j=1,2,…,N }Vi為凸多邊形,稱(chēng){Vi}mi=1為Dirichlet Tesselation 圖或?qū)ε嫉腣oronoi 圖。連接相鄰Voronoi 多邊形的內(nèi)核點(diǎn)可構(gòu)成三角形Tk,稱(chēng)集合{Tk} 為Delaunay 三角剖分。DT法的最大優(yōu)點(diǎn)是遵循“最小角最大”和“空球”準(zhǔn)則。因此,在各種二維三角剖分中,只有Delaunay三角剖分才同時(shí)滿足全局和局部最優(yōu)。“最小角最大”準(zhǔn)則是在不出現(xiàn)奇異性的情況下,Delaunay三角剖分最小角之和均大于任何非Delaunay剖分所形成三角形最小角之和。“空球”準(zhǔn)則是Delaunay三角剖分中任意三角形的外接圓(四面體為外接球)內(nèi)不包括其他結(jié)點(diǎn)。實(shí)現(xiàn)Delaunay三角剖分有多鐘方法,Lee和Schachter操作很有效,但很難實(shí)現(xiàn);而Watson、Cline和Renka、Sloan因操作容易、時(shí)間效率較好等優(yōu)點(diǎn)而被廣泛采用。為了進(jìn)一步提高效率,Sloan研究其算法操作,提出了時(shí)間復(fù)雜性為O(N)(N為結(jié)點(diǎn)總數(shù))的操作方法,從而為快速Delaunay 三角剖分提供了有效途徑。雖然DT法既適用于二維域也適用于三維域,但直接的Delaunay 三角剖分只適用于凸域,不適用于非凸域,因此發(fā)展了多種非凸域的Delaunay剖分。
AFM法的基本原理:設(shè)區(qū)域的有向離散外邊界集和邊界前沿點(diǎn)集已經(jīng)確定,按某種條件沿區(qū)域邊界向區(qū)域內(nèi)部扣除三角形(四面體)直到區(qū)域?yàn)榭占?/p>
AFM法的關(guān)鍵技術(shù)有兩個(gè):一是區(qū)域的邊界離散和和內(nèi)點(diǎn)的合理生成,二是扣除三角形條件。目前,扣除三角形的條件有多種。
最短距離條件。選取到該區(qū)域邊界前沿垂直距離最短的點(diǎn)或到邊界前沿端點(diǎn)距離平方和最小的點(diǎn)構(gòu)成三角形(四面體)。
最大角條件。在平面區(qū)域選與有向邊界前沿BC邊構(gòu)成角BAC最大的A點(diǎn))。實(shí)體區(qū)域選與有向邊界前沿三角形ABC構(gòu)成的四面體ABCD在D點(diǎn)實(shí)體角最大的點(diǎn)。這種選取點(diǎn)構(gòu)成三角形(四面體)方法可靠,但由于對(duì)應(yīng)于同一邊界前沿可能存在多個(gè)最大角情況,我們稱(chēng)這種現(xiàn)象為奇異現(xiàn)象。
最大形狀質(zhì)量條件。選取與邊界前沿所構(gòu)成的三角形(四面體)形狀質(zhì)量最大的點(diǎn)構(gòu)成有效剖分。
最小外接圓(球)條件,即空球條件。選取與邊界前沿構(gòu)成的三角形(四面體)中外接圓(球)半徑最小的點(diǎn)構(gòu)成有效剖分。即在所形成的三角形(四面體)中不包含任何其他邊界前沿點(diǎn)集。單一使用上述四種四面體扣除條件均會(huì)出現(xiàn)奇異情況。使用后兩者扣除單元都將可能引起剖分不可靠,如不可剖分及單元相交等。
AFM法最大優(yōu)點(diǎn)是,不僅在區(qū)域內(nèi)部而且在區(qū)域邊界所生成的網(wǎng)格單元形狀均優(yōu)良,網(wǎng)格生成全自動(dòng),可剖分任意實(shí)體。如果將板/殼、實(shí)體和梁采用統(tǒng)一的數(shù)據(jù)結(jié)構(gòu),則可采用該原理實(shí)現(xiàn)不同維數(shù)和多種材料等混合工況結(jié)構(gòu)件的網(wǎng)格自動(dòng)剖分。若配合誤差估計(jì),則這種方法在自適應(yīng)網(wǎng)格再生技術(shù)中使用效果甚佳。目前的發(fā)展趨勢(shì)是采用AFM/DT混合法。在平面域已得到了成功地實(shí)現(xiàn),但三維實(shí)體區(qū)域仍存在多種問(wèn)題,例如:可能出現(xiàn)剖分不可靠和奇異等現(xiàn)象。
四、自動(dòng)自適應(yīng)網(wǎng)格剖分
有限元的自適應(yīng)性就是在現(xiàn)有網(wǎng)格基礎(chǔ)上,根據(jù)有限元計(jì)算結(jié)果估計(jì)計(jì)算誤差、重新剖分網(wǎng)格和再計(jì)算的一個(gè)閉路循環(huán)過(guò)程。當(dāng)誤差達(dá)到預(yù)規(guī)定值時(shí),自適應(yīng)過(guò)程結(jié)束。因此,有效的誤差估計(jì)和良好的自適應(yīng)網(wǎng)格生成是自適應(yīng)有限元分析兩大關(guān)鍵技術(shù)。就目前國(guó)外研究來(lái)看,自動(dòng)自適應(yīng)網(wǎng)格生成從大的方面可分為:網(wǎng)格增加技術(shù)和網(wǎng)格再生技術(shù)。
1. 網(wǎng)格增加技術(shù)
該法主要依靠增加自由度總數(shù)來(lái)提高有限元分析的精度。目前主要采用三種類(lèi)型方法提高有限元分析精度:h-型、p-型和h-p-型。
h-型,采用有選擇地進(jìn)一步子劃分網(wǎng)格單元來(lái)細(xì)化網(wǎng)格以提高自由度。該法使用特別廣泛,RSD模型的網(wǎng)格改進(jìn)正是利用該法。
p-型,在保持網(wǎng)格劃分不變的情況下,通過(guò)提高插值函數(shù)的階數(shù)獲得高的求解精度。
h-p-型,是將h-型和p-型兩種結(jié)合的一種方法。該法雖然實(shí)現(xiàn)不容易,但它卻可使收斂速率明顯加快。
實(shí)踐表明,在獲得同一精度時(shí),上述三種類(lèi)型收斂速率是按h-型、p-型、h-p-型順序增加的。
2. 網(wǎng)格再生技術(shù)
根據(jù)現(xiàn)有網(wǎng)格并配合誤差估計(jì)確定新的結(jié)點(diǎn)密度分布,然后重新劃分網(wǎng)格,再計(jì)算并重復(fù)上述過(guò)程直到求解精度達(dá)到預(yù)定目標(biāo)為止。目前,網(wǎng)格再生技術(shù)在平面區(qū)域已得到了較好地實(shí)現(xiàn),現(xiàn)概括如下:
確定結(jié)點(diǎn)密度的最大和最小值。
按等比數(shù)列計(jì)算等值線分段總數(shù)N和每一條等值線結(jié)點(diǎn)密度值。
用N+1個(gè)結(jié)點(diǎn)密度將區(qū)域劃分為相應(yīng)的等值線。
光順每條等值線。消除等值線與區(qū)域邊界及等值線之間的尖角,并沿等值線生成結(jié)點(diǎn)。
形成封閉環(huán)。從內(nèi)部等值線和區(qū)域邊界中獲得邊界鏈,并按正確順序連接邊界鏈和內(nèi)部等值線鏈構(gòu)成封閉環(huán)。
形成子區(qū)域。子區(qū)域的結(jié)點(diǎn)密度等于區(qū)域邊界結(jié)點(diǎn)密度的平均值。
網(wǎng)格生成。采用二維平面網(wǎng)格生成方法構(gòu)成三角形。
從理論上講,該原理可擴(kuò)充到三維實(shí)體域,但由于三維實(shí)體域難以完全自動(dòng)用等結(jié)點(diǎn)密度曲面來(lái)分割任意實(shí)體,因此在三維域的擴(kuò)充至今仍未實(shí)現(xiàn)。實(shí)踐表明,網(wǎng)格再生技術(shù)比網(wǎng)格增加技術(shù)具有更大的優(yōu)點(diǎn),主要表現(xiàn)在前者收斂速度快、網(wǎng)格單元形狀穩(wěn)定。
另外,還有兩種自適應(yīng)網(wǎng)格生成類(lèi)型,它們是r-型和h-r-型。
r-型,是保持網(wǎng)格劃分和插值函數(shù)階數(shù)不變情況下,通過(guò)調(diào)整結(jié)點(diǎn)位置以改善求解精度。該法收斂速度低,因此,目前很少直接使用這種類(lèi)型。
h-r-型是上述r-型和h-型兩種方法的綜合。
事實(shí)上,在h-型網(wǎng)格改進(jìn)中所使用的光順技術(shù)就是一種r-型,所以可以把h-r-型看成是h-型。
編輯:fqj
-
網(wǎng)格
+關(guān)注
關(guān)注
0文章
139瀏覽量
16015 -
CAE
+關(guān)注
關(guān)注
0文章
76瀏覽量
23444
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
利用自適應(yīng)網(wǎng)格細(xì)化功能自動(dòng)生成最佳網(wǎng)格

鴻蒙原生開(kāi)發(fā)手記:01-元服務(wù)開(kāi)發(fā)
服務(wù)網(wǎng)格DPU卸載解決方案
使用FEMM(有限元法磁性學(xué))對(duì)電感式傳感器進(jìn)行仿真

導(dǎo)彈電磁彈射器有限元仿真及分析
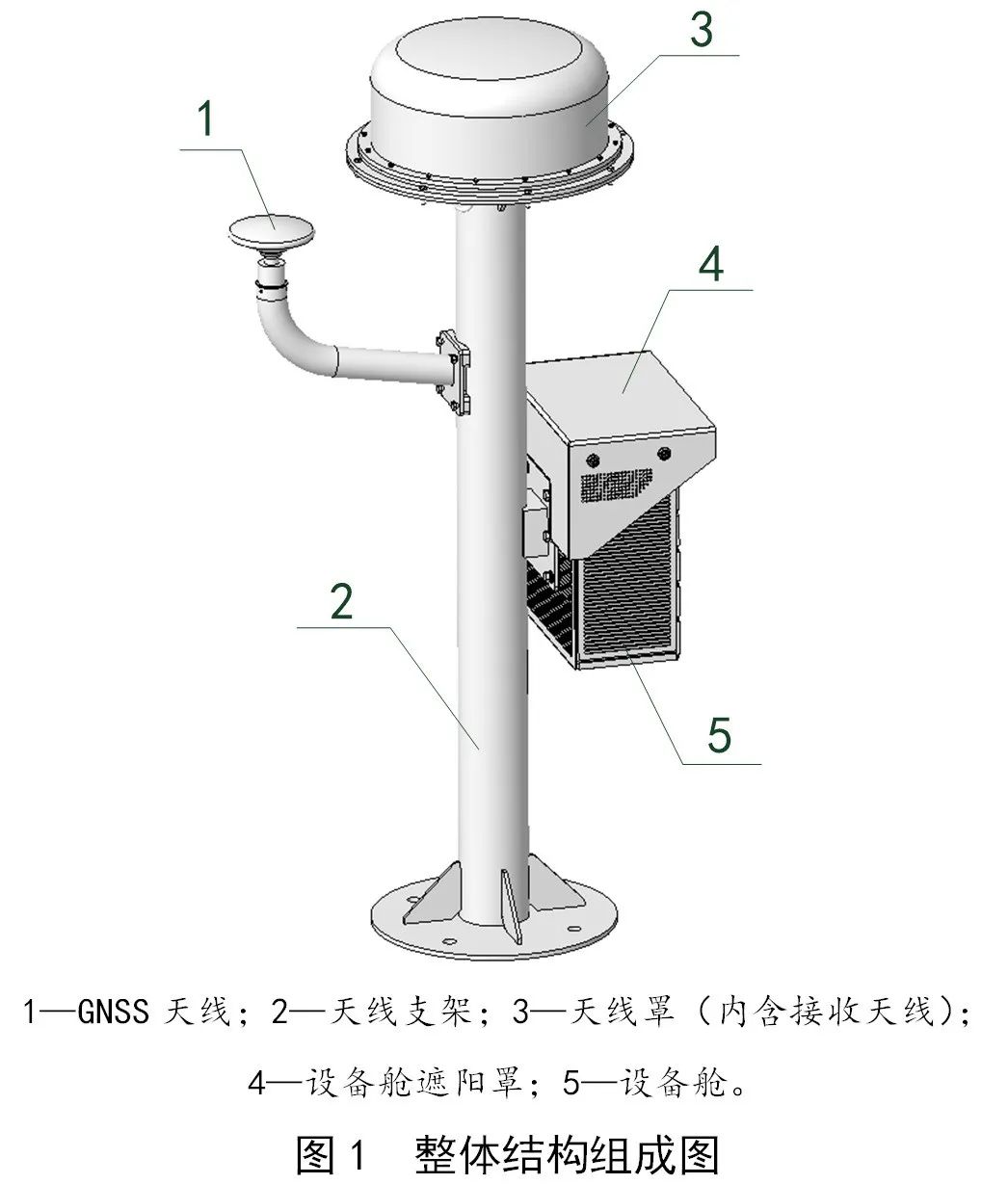
一種天線支架的結(jié)構(gòu)設(shè)計(jì)及有限元分析
電磁仿真軟件有哪些常用的方法
開(kāi)源!1000多元的高壓差分探頭,我花50元搞定了

Ansys Motion等速萬(wàn)向節(jié)剛?cè)狁詈蟿?dòng)力學(xué)仿真方案
基于有限元模型的IC 卡芯片受力分析研究

基于有限元模型的IC卡芯片受力分析研究

戴西軟件公司收購(gòu)PRESYS全球知識(shí)產(chǎn)權(quán):以通用有限元仿真軟件撬動(dòng)工業(yè)未來(lái)
Fidelity Pointwise中的自動(dòng)自適應(yīng)網(wǎng)格加密功能介紹




 有限元網(wǎng)格剖分原理的詳細(xì)介紹
有限元網(wǎng)格剖分原理的詳細(xì)介紹










評(píng)論