在播放視頻時,常遇到視頻尺寸與畫布尺寸不一致的情況。為了讓視頻按比例填充畫布,需要對視頻中的每一幀圖像做縮放處理。
縮放就是在原圖的基礎上做插值計算,從而增加或減少像素點的數量。常見的插值方式有最近點插值,線性插值,蘭索斯插值。
下面簡要介紹,并對比三種插值方式的結果。
最近點插值
在一維空間中,最近點插值就相當于四舍五入取整。在二維圖像中,像素點的坐標都是整數,該方法就是選取離目標點最近的點。計算方式如下:
假設原圖為A[aw,ah],寬度為aw,高度為ah。目標圖為B[bw,bh],寬度為bw,高度為bh。已知A[aw,ah]的寬度,高度及其中每個點的顏色值,B[bw,bh]中每個點像素值的計算方式如下:
for(int i=0; i<bh; ++i){
for(int j=0; j<bw; ++j){
int posX = floor(j/(float)bw * aw + 0.5f);
int posY = floor(i/(float)bh * ah + 0.5f);
B[i,j] = A[posY, posX];
}
}
線性插值
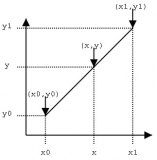
線性插值是以距離為權重的一種插值方式。在一維空間中,假設有點A,B,其距離為LAB。A,B之間任意一點C的值為A*LBC/LAB+B*LAC/LAB。在二維空間中,需要在兩個方向上做插值。
已知Q11,Q21,Q12,Q22,計算P點的值時,需要先由Q11和Q21插值得到R1,由Q12和Q22插值得到R2,再由R1和R2插值得到P。
詳情可參考:
https://zh.wikipedia.org/wiki/%E5%8F%8C%E7%BA%BF%E6%80%A7%E6%8F%92%E5%80%BC
該方法生成的圖像比較平滑
蘭索斯插值(lanczos)
一維的線性插值,是在目標點的左邊和右邊各取一個點做插值,這兩個點的權重是由線性函數計算得到。而一維的蘭索斯插值是在目標點的左邊和右邊各取四個點做插值,這八個點的權重是由高階函數計算得到。
詳細原理可查閱:
https://en.wikipedia.org/wiki/Lanczos_resampling
二維的蘭索斯插值在x,y方向分別對相鄰的八個點進行插值,也就是計算加權和,所以它是一個8x8的描述子。
網上目前可找到蘭索斯算法有兩份:GPUImage和OpenCV。其中GPUImage中是用GLSL實現,其算法有誤,并不能得到正確的結果。OpenCV中是用C++實現的CPU端代碼。
我參考OpenCV中的實現方式,實現了一份GPU上的蘭索斯插值算法,該算法在GPU上運行,并不額外消耗CPU資源。其對應的GLSL為
uniform int ssize;
uniform int tsize;
uniform int flag;
uniform float scale;
uniform sampler2D inputImageTexture;
void interpolateLanczos4(in float fx, inout float rate[8]) {
const float s45 = 0.70710678118654752440084436210485;
const float PI = 3.1415926535897932384626433832795;
float cs[] = float[16]( ,1.0, 0.0, -s45, -s45, 0.0, 1.0, s45, -s45, -1.0, 0.0, s45, s45, 0.0, -1.0, -s45, s45);
if( fx < 0.0000000001 ) {
for( int i = 0; i < 8; i++ ) {
rate[i] = 0.0;
}
rate[3] = 1.0;
return;
}
float sum = 0.0;
float y0 = -(fx+3.0)*PI*0.25;
float s0 = sin(y0);
float c0 = cos(y0);
for(int i = 0; i < 8; i++ ) {
float y = -(fx+float(3-i))*PI*0.25;
int index = i*2;
rate[i] = (cs[index]*s0 + cs[index+1]*c0) g (y*y);
sum += rate[i];
}
sum = 1.0gsum;
for(int i = 0; i < 8; i++ ) {
rate[i] *= sum;
}
}
void main() {
vec4 fragmentColor = vec4(0);
float curPos = float(tsize);
if( flag == 0 ) {
curPos = fragTexCoord.x * float(tsize);
} else {
curPos = fragTexCoord.y * float(tsize);
}
float fx = (curPos + 0.5) * scale - 0.5;
float sx = floor(fx);
fx -= sx;
float rate[8];
interpolateLanczos4(fx, rate);
for (int i=0; i<8; ++i) {
float newCoord = (sx + float(i - 3) ) / float(ssize);
vec2 texCoord;
if (flag == 0)
texCoord = vec2(newCoord, fragTexCoord.y);
else
texCoord = vec2(fragTexCoord.x, newCoord);
fragmentColor += texture2D(inputImageTexture, texCoord) * rate[i];
}
gl_FragColor = fragmentColor;
}
上述代碼需要執行兩遍:
第一遍的輸入為原圖,縮放寬度方向。ssize為原圖寬度,tsize為目標圖寬度。執行完畢后,把結果存到紋理中,作為第二遍的輸入;
第二遍縮放高度方向,ssize為原圖高度,tsize為目標圖高度。執行完畢后,把結果顯示到屏幕上。
結果對比
將上面的對比圖放大后可以發現,線性插值的結果較最近點插值更平滑,蘭索斯插值的結果較線性插值更清晰。
性能對比
運行環境:iphone5s,ios8.3
運行程序:自研播放器demo
以上三種插值算法渲染每幀圖像時,占用CPU時間都是40ms左右。由于這三種算法都是在GPU上實現,其對應的CPU代碼相同,結果與預期相符。
占用GPU時間如下所示:
| 插值方式 | 最近點插值 | 線性插值 | 蘭索斯插值 |
| 每幀圖像平均占用的GPU時間(ms) | 6 | 6 | 12 |
蘭索斯插值算法占用GPU的平均時間為12ms,是其它兩種算法的兩倍,由于該算法中shader代碼執行了兩遍,結果也與預期相符。
由于GPU與CPU是異步執行,大部分視頻幀率不超過30,因此GPU上多出的6ms不會造成性能瓶頸。
注:GPUImage中的蘭索斯插值實現有誤,本文是參考OpenCV實現的。
作者:梧桐光影
鏈接:https://www.jianshu.com/p/8ae52a88ca61
責任編輯:haq
-
視頻
+關注
關注
6文章
1942瀏覽量
72885 -
圖像
+關注
關注
2文章
1083瀏覽量
40449
原文標題:三種圖像插值方式對比
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于OpenCV的拆分和合并圖像通道實驗案例分享_基于RK3568教學實驗箱
DAC39J84使用插值模式遇到的疑問求解
DSP教學實驗箱_數字圖像處理操作_案例分享:5-13 灰度圖像二值化
基于FPGA的實時邊緣檢測系統設計,Sobel圖像邊緣檢測,FPGA圖像處理
如何在labview FPGA端實現二維插值的功能?
FPGA驅動下的視頻圖像拼接融合技術革新
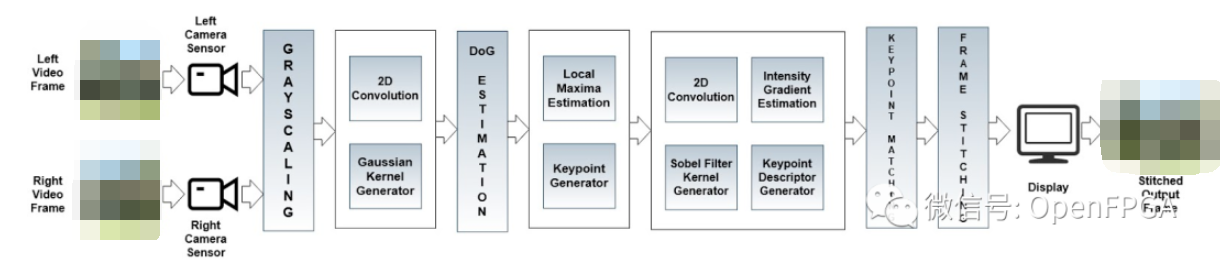




 視頻圖像三插值方式的結果
視頻圖像三插值方式的結果











評論