二叉樹上應該怎么求,二叉搜索樹上又應該怎么求?
在求眾數集合的時候有一個技巧,因為題目中眾數是可以有多個的,所以一般的方法需要遍歷兩遍才能求出眾數的集合。
但可以遍歷一遍就可以求眾數集合,使用了適時清空結果集的方法,這個方法還是很巧妙的。相信仔細讀了文章的同學會驚呼其巧妙!
501.二叉搜索樹中的眾數
題目鏈接:https://leetcode-cn.com/problems/find-mode-in-binary-search-tree/solution
給定一個有相同值的二叉搜索樹(BST),找出 BST 中的所有眾數(出現頻率最高的元素)。
假定 BST 有如下定義:
- 結點左子樹中所含結點的值小于等于當前結點的值
- 結點右子樹中所含結點的值大于等于當前結點的值
- 左子樹和右子樹都是二叉搜索樹
例如:
給定 BST [1,null,2,2],
返回[2].
提示:如果眾數超過1個,不需考慮輸出順序
進階:你可以不使用額外的空間嗎?(假設由遞歸產生的隱式調用棧的開銷不被計算在內)
思路
這道題目呢,遞歸法我從兩個維度來講。
首先如果不是二叉搜索樹的話,應該怎么解題,是二叉搜索樹,又應該如何解題,兩種方式做一個比較,可以加深大家對二叉樹的理解。
遞歸法
如果不是二叉搜索樹
如果不是二叉搜索樹,最直觀的方法一定是把這個樹都遍歷了,用map統計頻率,把頻率排個序,最后取前面高頻的元素的集合。
具體步驟如下:
- 這個樹都遍歷了,用map統計頻率
至于用前中后序那種遍歷也不重要,因為就是要全遍歷一遍,怎么個遍歷法都行,層序遍歷都沒毛病!
這里采用前序遍歷,代碼如下:
//mapkey:元素,value:出現頻率
voidsearchBST(TreeNode*cur,unordered_map<int,int>&map){//前序遍歷
if(cur==NULL)return;
map[cur->val]++;//統計元素頻率
searchBST(cur->left,map);
searchBST(cur->right,map);
return;
}
- 把統計的出來的出現頻率(即map中的value)排個序
有的同學可能可以想直接對map中的value排序,還真做不到,C++中如果使用std::map或者std::multimap可以對key排序,但不能對value排序。
所以要把map轉化數組即vector,再進行排序,當然vector里面放的也是pair類型的數據,第一個int為元素,第二個int為出現頻率。
代碼如下:
boolstaticcmp(constpair&a,constpair&b){
returna.second>b.second;//按照頻率從大到小排序
}
vector>vec(map.begin(),map.end());
sort(vec.begin(),vec.end(),cmp);//給頻率排個序
- 取前面高頻的元素
此時數組vector中已經是存放著按照頻率排好序的pair,那么把前面高頻的元素取出來就可以了。
代碼如下:
result.push_back(vec[0].first);
for(inti=1;i//取最高的放到result數組中
if(vec[i].second==vec[0].second)result.push_back(vec[i].first);
elsebreak;
}
returnresult;
整體C++代碼如下:
classSolution{
private:
voidsearchBST(TreeNode*cur,unordered_map<int,int>&map){//前序遍歷
if(cur==NULL)return;
map[cur->val]++;//統計元素頻率
searchBST(cur->left,map);
searchBST(cur->right,map);
return;
}
boolstaticcmp(constpair<int,int>&a,constpair<int,int>&b){
returna.second>b.second;
}
public:
vector<int>findMode(TreeNode*root){
unordered_map<int,int>map;//key:元素,value:出現頻率
vector<int>result;
if(root==NULL)returnresult;
searchBST(root,map);
vectorint ,int>>vec(map.begin(),map.end());
sort(vec.begin(),vec.end(),cmp);//給頻率排個序
result.push_back(vec[0].first);
for(inti=1;i//取最高的放到result數組中
if(vec[i].second==vec[0].second)result.push_back(vec[i].first);
elsebreak;
}
returnresult;
}
};
所以如果本題沒有說是二叉搜索樹的話,那么就按照上面的思路寫!
是二叉搜索樹
既然是搜索樹,它中序遍歷就是有序的。
中序遍歷代碼如下:
voidsearchBST(TreeNode*cur){
if(cur==NULL)return;
searchBST(cur->left);//左
(處理節點)//中
searchBST(cur->right);//右
return;
}
遍歷有序數組的元素出現頻率,從頭遍歷,那么一定是相鄰兩個元素作比較,然后就把出現頻率最高的元素輸出就可以了。
關鍵是在有序數組上的話,好搞,在樹上怎么搞呢?
這就考察對樹的操作了。
在二叉樹:搜索樹的最小絕對差中我們就使用了pre指針和cur指針的技巧,這次又用上了。
弄一個指針指向前一個節點,這樣每次cur(當前節點)才能和pre(前一個節點)作比較。
而且初始化的時候pre = NULL,這樣當pre為NULL時候,我們就知道這是比較的第一個元素。
代碼如下:
if(pre==NULL){//第一個節點
count=1;//頻率為1
}elseif(pre->val==cur->val){//與前一個節點數值相同
count++;
}else{//與前一個節點數值不同
count=1;
}
pre=cur;//更新上一個節點
此時又有問題了,因為要求最大頻率的元素集合(注意是集合,不是一個元素,可以有多個眾數),如果是數組上大家一般怎么辦?
應該是先遍歷一遍數組,找出最大頻率(maxCount),然后再重新遍歷一遍數組把出現頻率為maxCount的元素放進集合。(因為眾數有多個)
這種方式遍歷了兩遍數組。
那么我們遍歷兩遍二叉搜索樹,把眾數集合算出來也是可以的。
但這里其實只需要遍歷一次就可以找到所有的眾數。
那么如何只遍歷一遍呢?
如果 頻率count 等于 maxCount(最大頻率),當然要把這個元素加入到結果集中(以下代碼為result數組),代碼如下:
if(count==maxCount){//如果和最大值相同,放進result中
result.push_back(cur->val);
}
是不是感覺這里有問題,result怎么能輕易就把元素放進去了呢,萬一,這個maxCount此時還不是真正最大頻率呢。
所以下面要做如下操作:
頻率count 大于 maxCount的時候,不僅要更新maxCount,而且要清空結果集(以下代碼為result數組),因為結果集之前的元素都失效了。
if(count>maxCount){//如果計數大于最大值
maxCount=count;//更新最大頻率
result.clear();//很關鍵的一步,不要忘記清空result,之前result里的元素都失效了
result.push_back(cur->val);
}
關鍵代碼都講完了,完整代碼如下:(只需要遍歷一遍二叉搜索樹,就求出了眾數的集合)
classSolution{
private:
intmaxCount;//最大頻率
intcount;//統計頻率
TreeNode*pre;
vector<int>result;
voidsearchBST(TreeNode*cur){
if(cur==NULL)return;
searchBST(cur->left);//左
//中
if(pre==NULL){//第一個節點
count=1;
}elseif(pre->val==cur->val){//與前一個節點數值相同
count++;
}else{//與前一個節點數值不同
count=1;
}
pre=cur;//更新上一個節點
if(count==maxCount){//如果和最大值相同,放進result中
result.push_back(cur->val);
}
if(count>maxCount){//如果計數大于最大值頻率
maxCount=count;//更新最大頻率
result.clear();//很關鍵的一步,不要忘記清空result,之前result里的元素都失效了
result.push_back(cur->val);
}
searchBST(cur->right);//右
return;
}
public:
vector<int>findMode(TreeNode*root){
count=0;
maxCount=0;
TreeNode*pre=NULL;//記錄前一個節點
result.clear();
searchBST(root);
returnresult;
}
};
迭代法
只要把中序遍歷轉成迭代,中間節點的處理邏輯完全一樣。
二叉樹前中后序轉迭代,傳送門:
下面我給出其中的一種中序遍歷的迭代法,其中間處理邏輯一點都沒有變(我從遞歸法直接粘過來的代碼,連注釋都沒改,哈哈)
代碼如下:
classSolution{
public:
vector<int>findMode(TreeNode*root){
stackst;
TreeNode*cur=root;
TreeNode*pre=NULL;
intmaxCount=0;//最大頻率
intcount=0;//統計頻率
vector<int>result;
while(cur!=NULL||!st.empty()){
if(cur!=NULL){//指針來訪問節點,訪問到最底層
st.push(cur);//將訪問的節點放進棧
cur=cur->left;//左
}else{
cur=st.top();
st.pop();//中
if(pre==NULL){//第一個節點
count=1;
}elseif(pre->val==cur->val){//與前一個節點數值相同
count++;
}else{//與前一個節點數值不同
count=1;
}
if(count==maxCount){//如果和最大值相同,放進result中
result.push_back(cur->val);
}
if(count>maxCount){//如果計數大于最大值頻率
maxCount=count;//更新最大頻率
result.clear();//很關鍵的一步,不要忘記清空result,之前result里的元素都失效了
result.push_back(cur->val);
}
pre=cur;
cur=cur->right;//右
}
}
returnresult;
}
};
總結
本題在遞歸法中,我給出了如果是普通二叉樹,應該怎么求眾數。
知道了普通二叉樹的做法時候,我再進一步給出二叉搜索樹又應該怎么求眾數,這樣鮮明的對比,相信會對二叉樹又有更深層次的理解了。
在遞歸遍歷二叉搜索樹的過程中,我還介紹了一個統計最高出現頻率元素集合的技巧, 要不然就要遍歷兩次二叉搜索樹才能把這個最高出現頻率元素的集合求出來。
為什么沒有這個技巧一定要遍歷兩次呢?因為要求的是集合,會有多個眾數,如果規定只有一個眾數,那么就遍歷一次穩穩的了。
最后我依然給出對應的迭代法,其實就是迭代法中序遍歷的模板加上遞歸法中中間節點的處理邏輯,分分鐘就可以寫出來,中間邏輯的代碼我都是從遞歸法中直接粘過來的。
求二叉搜索樹中的眾數其實是一道簡單題,但大家可以發現我寫了這么一大篇幅的文章來講解,主要是為了盡量從各個角度對本題進剖析,幫助大家更快更深入理解二叉樹。
需要強調的是 leetcode上的耗時統計是非常不準確的,看個大概就行,一樣的代碼耗時可以差百分之50以上,所以leetcode的耗時統計別太當回事,知道理論上的效率優劣就行了。
其他語言版本
Java
暴力法
classSolution{
publicint[]findMode(FindModeInBinarySearchTree.TreeNoderoot){
Mapmap=newHashMap<>();
Listlist=newArrayList<>();
if(root==null)returnlist.stream().mapToInt(Integer::intValue).toArray();
//獲得頻率Map
searchBST(root,map);
List>mapList=map.entrySet().stream()
.sorted((c1,c2)->c2.getValue().compareTo(c1.getValue()))
.collect(Collectors.toList());
list.add(mapList.get(0).getKey());
//把頻率最高的加入list
for(inti=1;iif(mapList.get(i).getValue()==mapList.get(i-1).getValue()){
list.add(mapList.get(i).getKey());
}else{
break;
}
}
returnlist.stream().mapToInt(Integer::intValue).toArray();
}
voidsearchBST(FindModeInBinarySearchTree.TreeNodecurr,Mapmap) {
if(curr==null)return;
map.put(curr.val,map.getOrDefault(curr.val,0)+1);
searchBST(curr.left,map);
searchBST(curr.right,map);
}
}
classSolution{
ArrayListresList;
intmaxCount;
intcount;
TreeNodepre;
publicint[]findMode(TreeNoderoot){
resList=newArrayList<>();
maxCount=0;
count=0;
pre=null;
findMode1(root);
int[]res=newint[resList.size()];
for(inti=0;ireturnres;
}
publicvoidfindMode1(TreeNoderoot){
if(root==null){
return;
}
findMode1(root.left);
introotValue=root.val;
//計數
if(pre==null||rootValue!=pre.val){
count=1;
}else{
count++;
}
//更新結果以及maxCount
if(count>maxCount){
resList.clear();
resList.add(rootValue);
maxCount=count;
}elseif(count==maxCount){
resList.add(rootValue);
}
pre=root;
findMode1(root.right);
}
}
Python
遞歸法
classSolution:
deffindMode(self,root:TreeNode)->List[int]:
ifnotroot:return
self.pre=root
self.count=0//統計頻率
self.countMax=0//最大頻率
self.res=[]
deffindNumber(root):
ifnotroot:returnNone//第一個節點
findNumber(root.left)//左
ifself.pre.val==root.val://中:與前一個節點數值相同
self.count+=1
else://與前一個節點數值不同
self.pre=root
self.count=1
ifself.count>self.countMax://如果計數大于最大值頻率
self.countMax=self.count//更新最大頻率
self.res=[root.val]//更新res
elifself.count==self.countMax://如果和最大值相同,放進res中
self.res.append(root.val)
findNumber(root.right)//右
return
findNumber(root)
returnself.res
迭代法-中序遍歷-不使用額外空間,利用二叉搜索樹特性
classSolution:
deffindMode(self,root:TreeNode)->List[int]:
stack=[]
cur=root
pre=None
maxCount,count=0,0
res=[]
whilecurorstack:
ifcur:#指針來訪問節點,訪問到最底層
stack.append(cur)
cur=cur.left
else:#逐一處理節點
cur=stack.pop()
ifpre==None:#第一個節點
count=1
elifpre.val==cur.val:#與前一個節點數值相同
count+=1
else:
count=1
ifcount==maxCount:
res.append(cur.val)
ifcount>maxCount:
maxCount=count
res.clear()
res.append(cur.val)
pre=cur
cur=cur.right
returnres
-
SQL
+關注
關注
1文章
768瀏覽量
44175 -
二叉樹
+關注
關注
0文章
74瀏覽量
12348
原文標題:二叉搜索樹中的眾數是多少?
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
ATA-2041高壓放大器在叉指形電極管狀壓電元件電極制備中的應用

鐳神智能機器人三向叉式3D SLAM無人叉車:重塑高位堆垛與窄通道倉儲新境界

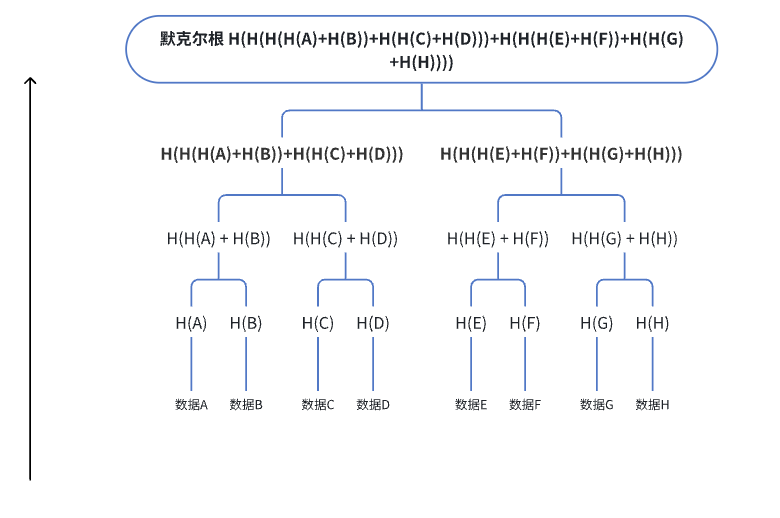
什么是默克爾樹(Merkle Tree)?如何計算默克爾根?
二極管電路求輸出電壓不用管電阻嗎
海康機器人推出全新一代潛伏叉取式機器人
多叉指MOSFET器件靜電防護魯棒性提升技巧
esp32c3運行examples/wifi/getting_started/softAP例子,設置密碼后WIFI標志上顯示一個叉,為什么?
求遠電子推出一款基于MC33774的ESS工商儲BMS方案




 二叉樹上應該怎么求
二叉樹上應該怎么求












評論