原文來自公眾號：工程師看海

調制與解調是通訊中非常常見的技術，其實在微弱信號采集中也會用到此技術，那么調制與解調究竟是怎么一回事呢？關注公眾號：工程師看海，讓我帶你慢慢研究。

調制與解調，可以用四個字概括其原理：頻譜搬移。

公眾號后臺回復：調制解調

可獲得基于matlab的仿真代碼

1. 讓我們先建立直觀應用概念，以調幅調制為例，理解調制解調的作用結果，然后再來從原理進行分析。

例1：微弱信號放大。

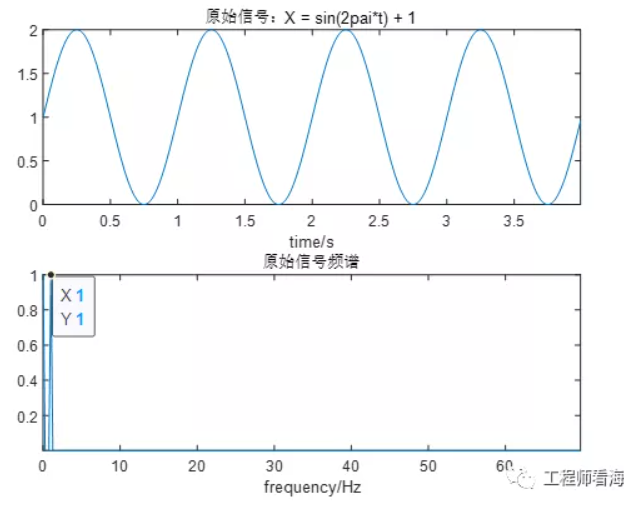
假如當前有一信號X = sin(2πt)+ 1；其包含了一個1V的直流成分，時域、頻域波形見下圖。

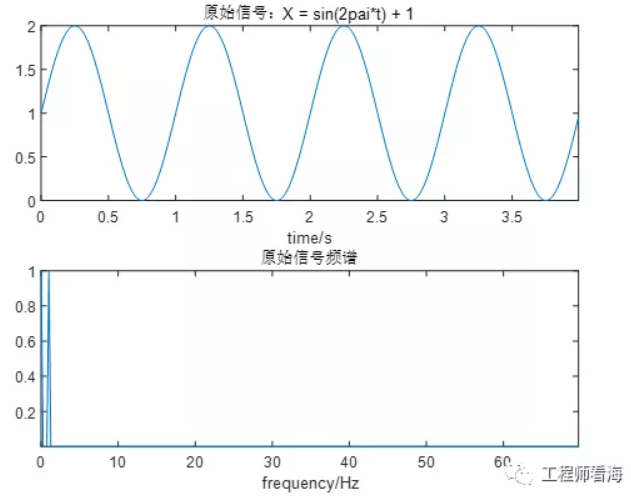
如果想去直接放大原始信號，那么它包含的直流信號也會被直接放大，后續電路可能主要處理放大后的直流，甚至會進入非線性區域，影響后續電路正常工作。

我們可以加一個隔直電容，或高通電路，來抑制這個直流，然后在進行交流放大，然而這個缺點是對于有一定帶寬的信號，在去除直流成分的同時，也去除了一部分有用的低頻信號，傷敵1000自損800，這是我們不希望看到的。

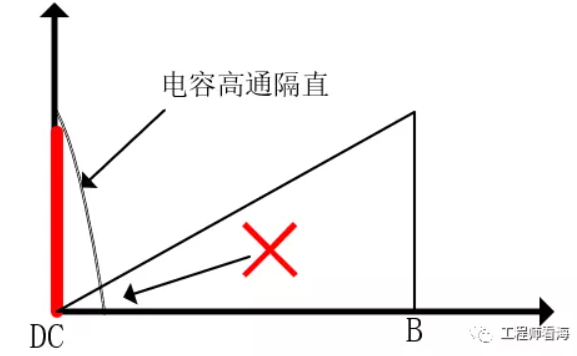
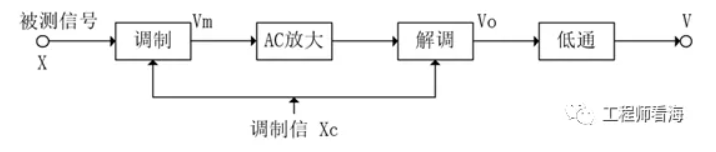
調制與解調為此給出了一種解決方案，其思路是用一個高頻信號去調制我們采集的原始信號，把原始信號的頻譜搬移到高頻去，經過AC放大后，再把頻譜搬移回去，實現放大的目的，一箭雙雕。

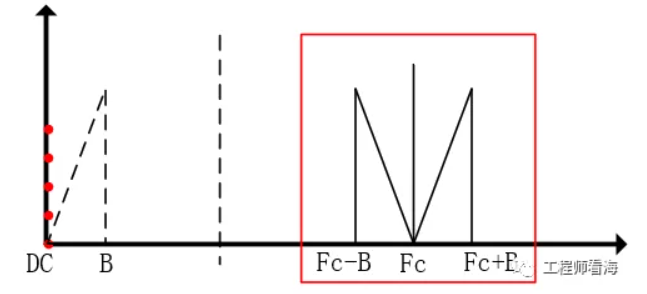
現在我們用一個高頻信號去調制原始信號，其過程就是用頻率為Fc的高頻信號Xc去乘原始信號X，這個高頻Fc的頻率要遠大于原始信號的頻率。

從下圖可以看出，調制后的信號以Fc為載波，頻譜被搬移到了高頻，我們此時可以對其進行放大。如果電路里又引入低頻干擾，此時就可以用隔直電容，因為此時低頻直流與目標信號頻帶（Fc±B）已經分離，對引入的直流隔直，就不會造成影響。

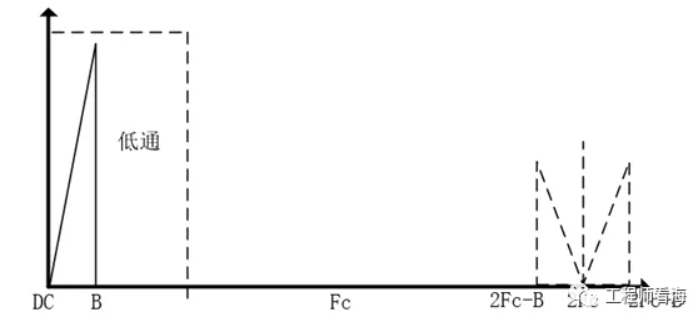
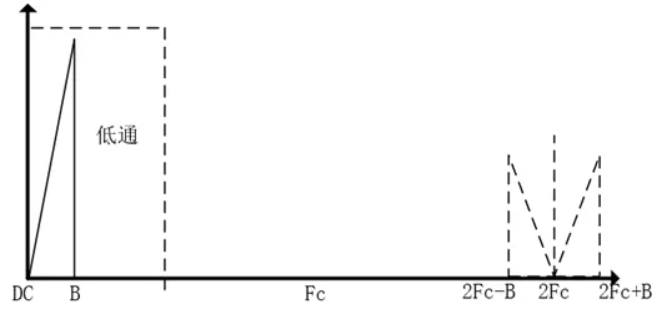
經過調制->AC放大->隔直后的信號，再經過解調，也就是再次頻譜搬移后，就又回到原始的頻帶，雖然增加了（2Fc±B）的成分，只要對其進行低通濾波去除新增的高頻部分，就可以實現放大的初衷了。

2. 原理解析。

設目標信號為X = cos(2πB*t)，其頻率為B，調制信號Xc=cos(2πFc*t)，其頻率為Fc。

二者調制后

Vm = X*Xc = cos(2πB*t)*cos(2πFc*t) = 0.5cos(2π(Fc+B)t)+ 0.5cos(2π(Fc-B)t)，(高中知識哦，不要說以前的知識沒用哦)，我們觀察Vm中信號的頻帶是Fc+B與Fc-B。

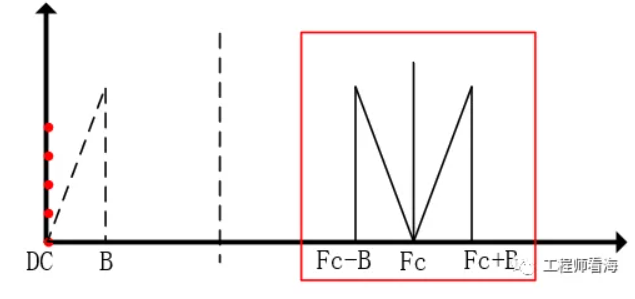
對Vm進行A倍AC放大后，就可以用隔直電容或高通濾除低頻部分。然后再對Vm進行解調，即再乘下調制信號Xc，得到輸出Vo，解調過程為:

Vo = Vm * Xc = A*[0.5cos(2π(Fc+B)t) + 0.5cos(2π(Fc-B)t) ] * cos(2πFc*t) = 0.25A[cos(2π(2Fc+B)t) + cos(2π(2Fc-B)t) + 2cos(2πB*t)]

Vo包含了高頻也包含了原始頻帶，對其進行低通后，就可以得到放大后的信號啦。

總結調制與解調過程如下：

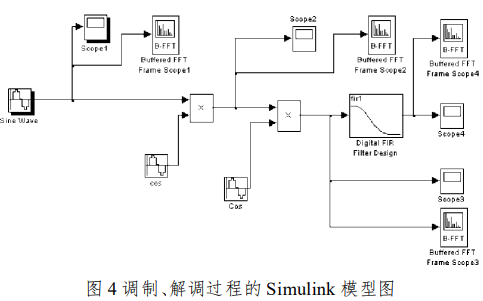
3.Matlab 仿真

公眾號后臺回復：調制解調

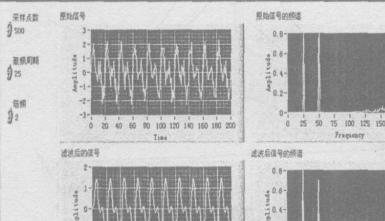
仿真原始信號是(AC1V+DC1V)&1Hz的交流信號

用頻率為30Hz的載波調至后，頻率被搬移到30Hz±1Hz的位置了，對其進行5倍放大，調制并放大后的時域波形看，其幅值比原始信號要小。

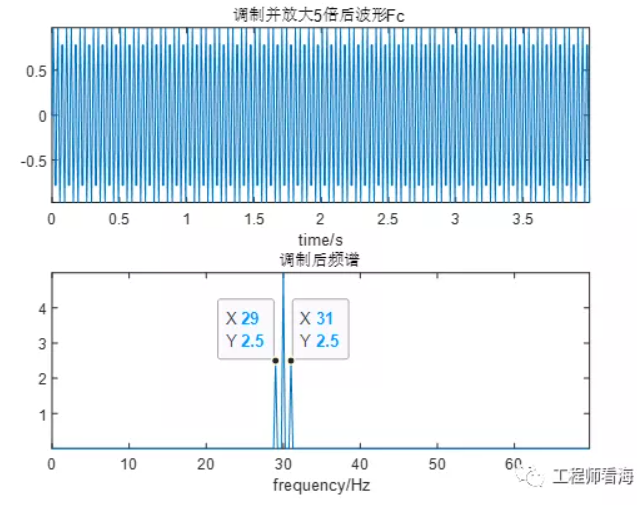
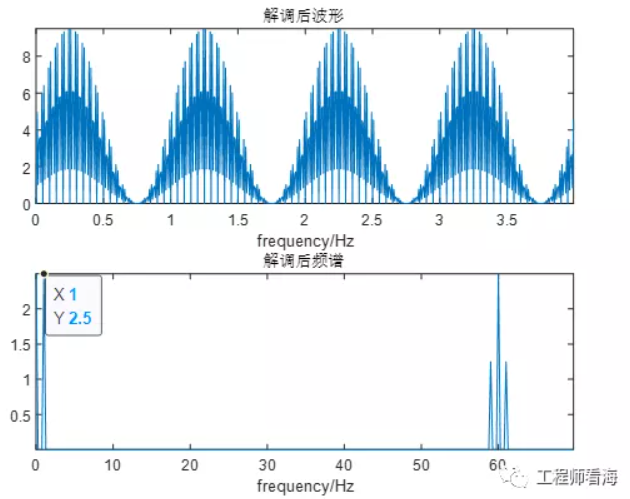
然后對信號解調，再次頻譜搬移。原始(AC1V+DC1V)&1Hz的信號，在低頻處變為1Hz&(0.25*5*2)=2.5V，與前文理論分析結果一致。

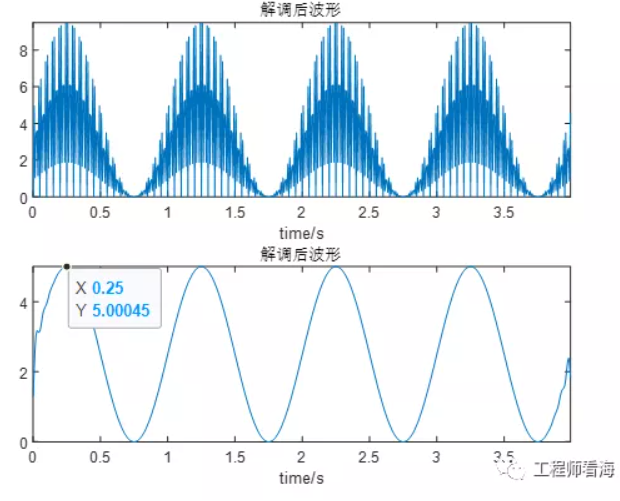
經過低通濾波后的波形如下：

以上就是調制解調的原理介紹，感謝點贊、在看、分享，讓知識變得更簡單。

歡迎加入工程師看海技術交流群添加小編微信：chunhou0820（備注：進群）

推薦閱讀▼

電池、電源

硬件文章精選

華為海思軟硬件開發資料