本文將從通俗的角度看待拉普拉斯變換。
發明者
奧列弗.赫維賽德,維多利亞時期英國人,全靠自學,聽力殘疾。很多人熟悉赫維賽德是因為MATLAB有一個赫維賽德(Heaviside)函數。
赫維賽德簡化了麥克斯韋方程組:即變化的電場產生磁場,變化的磁場產生電場。讓20個方程組便成了4個。
**赫維賽德另一個貢獻就是我們今天要說的運算微積分-它可以將常微分方程轉換為普通代數方程。**赫維賽德是怎么解微分方程的呢?他把微分、積分運算用一個簡單的算子來代替。

也就是說,在某種算子下,積分和微分對應的是倒數關系,至于算子 p 代表什么,赫維賽德也沒有多解釋,在缺乏嚴密數學基礎的情況下,人家直接放在文章就用了,還發表了。比如常見的一個二階常微分方程,
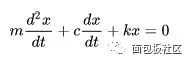
如果用赫維賽德的微分算子變換一下,就變成了代數表達式。
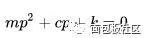
赫維賽德之所以這么做,是因為他的“物理直覺”告訴他這么做,就是這么硬。這顯然是一種開外掛的行為,因此也受到當時的主流數學家們們的攻訐,他們認為赫維賽德就是十足的“民科”,文章沒什么理論依據,自己在那空想呢。當然,赫維賽德也不是弱雞,科學家懟起人來,也是毫不含糊:“因為我不能理解消化過程就拒絕晚餐嗎?不,只要我滿意這個結果。”
好了,扯了那么遠,有童鞋已經不耐心了:這些和拉普拉斯變換有什么關系?謎底就是:赫維賽德的微積分算子,就是拉普拉斯變換的前身。
傅里葉變換(輕量版拉普拉斯變換)
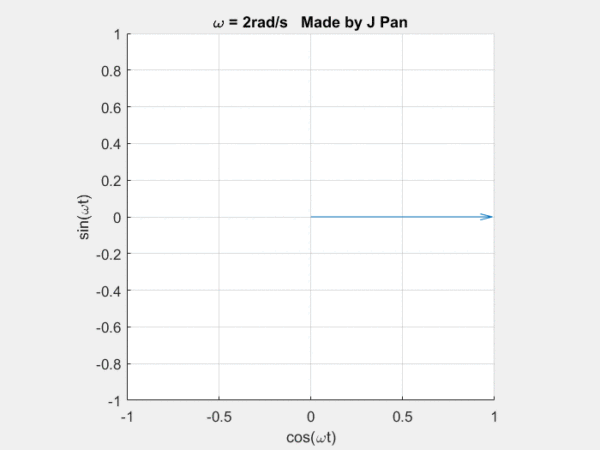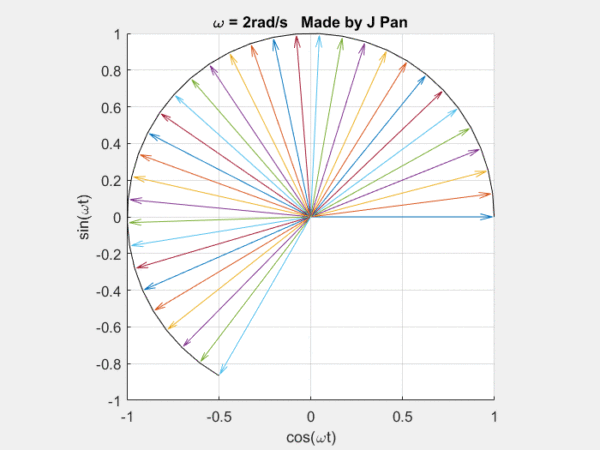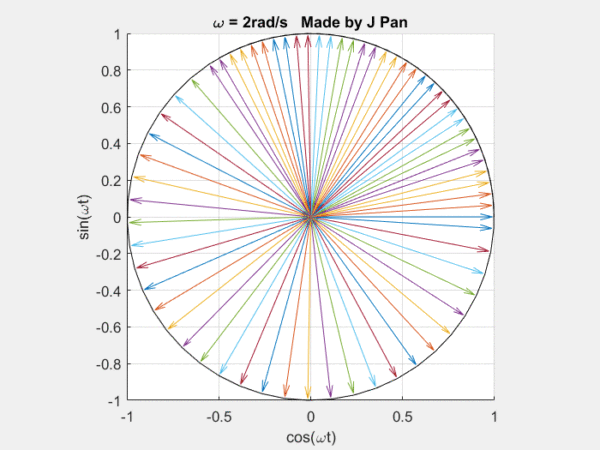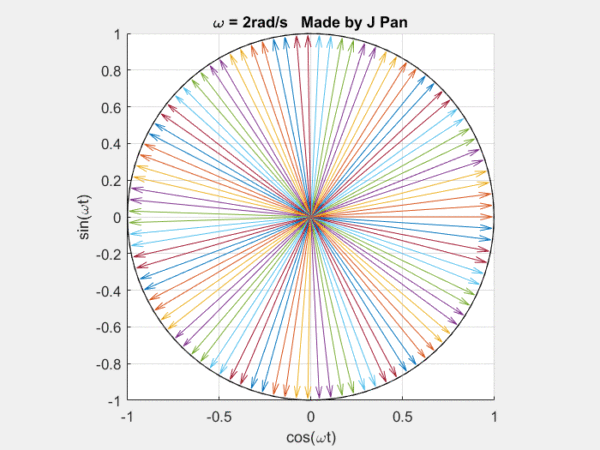
在說拉普拉斯變換以前,我們要先提一下傅里葉變換,這可以看成是輕量版的拉普拉斯變換。傅里葉變換說的是什么事?說的是自然界的很多現象,都可以用三角函數進行分解。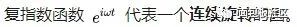
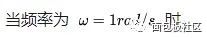
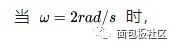
clc;clear;
h = animatedline;
xl=xlabel('cos(omegat)');%
yl=ylabel('sin(omegat)');%
grid on;
title('omega = 1rad/s Made by J Pan')
axis([-1,1,-1,1]);
axis square;
N = 100;
t=linspace(0,2*pi,N);
w=1;
x=cos(w*t);
y=sin(w*t);
a = tic; % start timer
for k = 1:N
addpoints(h,x(k),y(k));
hold on
quiver(0,0,x(k)*1.1,y(k)*1.1)
b = toc(a); % check timer
if b > (1/90)
drawnow % update screen every 1/30 seconds
a = tic; % reset timer after updating
end
end

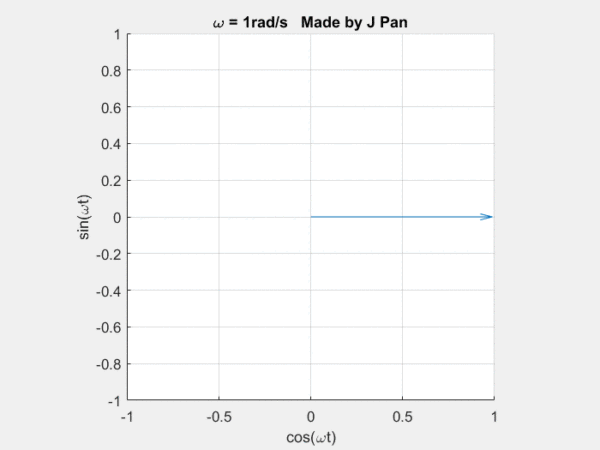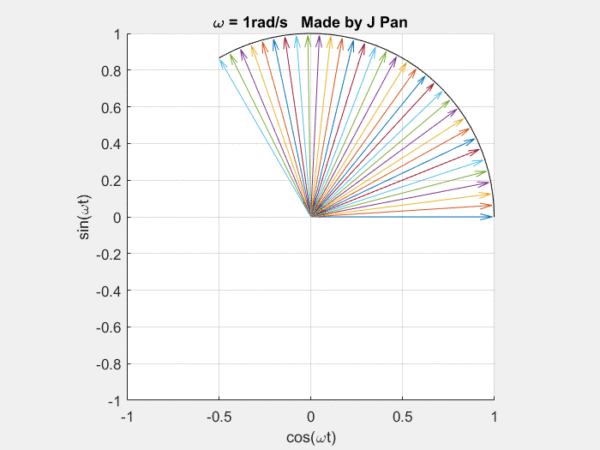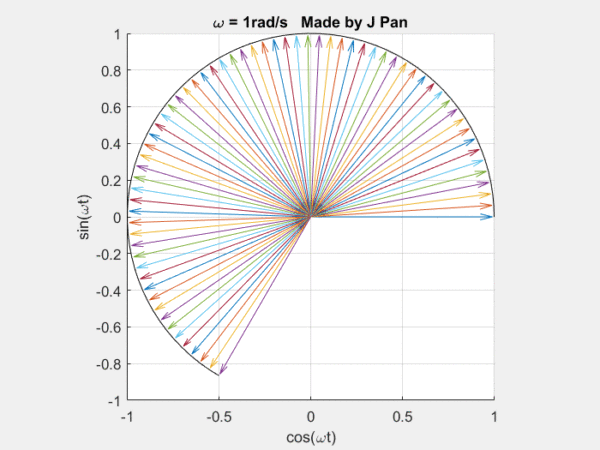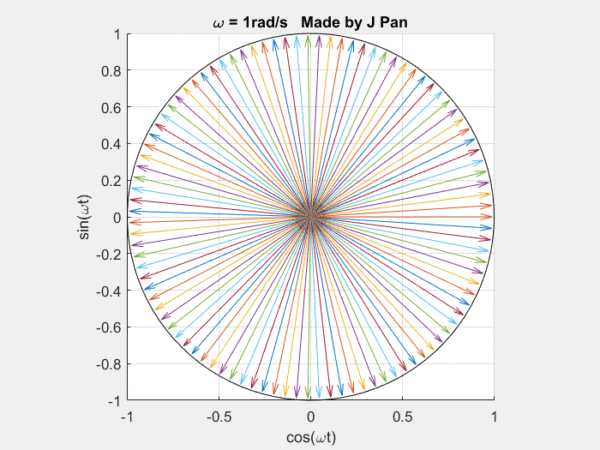
你能想象到很多曲線,都可以用這些不同頻率,連續旋轉的圓,通過線性疊加得到,而傅里葉定律,就是對這個結論的數學描述。
傅里葉定律說:只要一個函數滿足如狄利赫里條件,都能分解為復指數函數之和,哪怕是如拉格朗日提到的帶有棱角的方波函數。狄利赫里條件為:

其中可去間斷點和跳躍間斷點屬于第一類間斷點
于是就可以很好的解釋拉格朗日和傅里葉之間的爭論了——拉格朗日是對的:正弦曲線無法組合成一個帶有棱角的信號,棱角處會有很小高頻波動(吉布斯現象)。但是,我們可以用正弦曲線來非常逼近地表示它,逼近到兩種表示方法不存在能量差別,基于此,傅里葉也是對的。一個從數學家的角度,一個從工程師的角度。
拉普拉斯變換-原來就是這么回事
傅里葉變換能幫我們解決很多問題,一經問世后便受到廣大工程師們的喜愛,因為它給人們提供了一扇不同的窗戶來觀察世界,從這個窗戶來看,很多事情往往變得簡單多了。但是,別忘了,傅里葉變換有一個很大局限性,那就是信號必須滿足狄利赫里條件才行,特別是那個絕對可積的條件,一下子就攔截掉了一大批函數。比如函數 f(t)=t^2 就無法進行傅里葉變換。這點難度當然拿不到聰明的數學家們,他們想到了一個絕佳的主意:把不滿足絕對的可積的函數乘以一個快速衰減的函數,這樣在趨于無窮 時原函數也衰減到零了,從而滿足絕對可積。
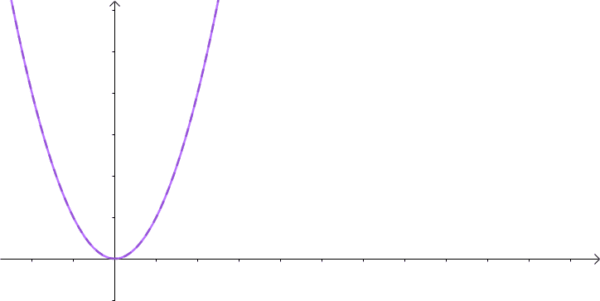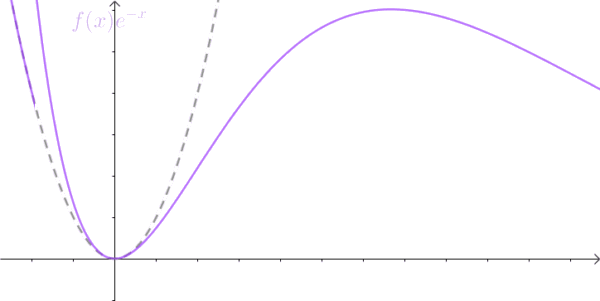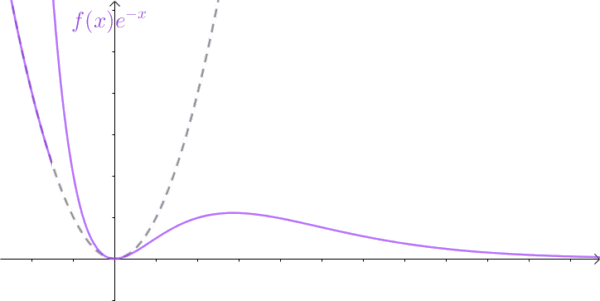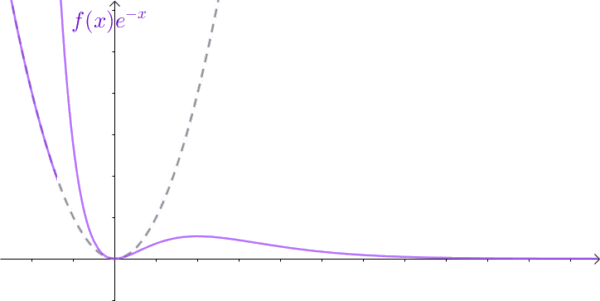

這里我要補充一下,不是為了保證一直為衰減,指數函數,要衰減,在負半軸也是衰減的,要增加,在正負半軸都是增加的。是因為在我們關心的系統中,不對時間的負半軸作分析。因此,我們更多使用單邊的拉普拉斯變換,而不是使用雙邊的拉普拉斯變換,這樣的系統稱之為因果系統不需要考慮 t=0 時的系統初始條件。
我知道大部分人前面的數學推導沒什么興趣,接下來就是放彩蛋的時刻了,很多童鞋會說不管傅里葉變換或者拉普拉斯變換是什么細節,你能說點有意思的,讓人能記憶深刻的信息嗎?

clc;clear;
h = animatedline;
h1=gcf;
view(3);
xl=xlabel('cos(omegat)');%
yl=ylabel('sin(omegat)');%
zl=zlabel('t');%
set(xl,'Rotation',30);%
set(yl,'Rotation',-30);%
grid on;
title('omega = 1rad/s Made by J Pan')
axis([-1,1,-1,1,0,4*pi])
N = 200;
t=linspace(0,4*pi,N);
w=1;
x=cos(w*t);
y=sin(w*t);
a = tic; % start timer
for k = 1:N
addpoints(h,x(k),y(k),t(k));
hold on
line([0 x(k)],[0 y(k)],[t(k) t(k)],'Color','red')
b = toc(a); % check timer
if b > (1/90)
drawnow % update screen every 1/30 seconds
a = tic; % reset timer after updating
end
end
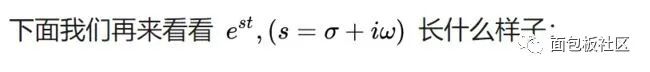
clc;clear;
h = animatedline;
h1=gcf;
view(3);
xl=xlabel('cos(omegat)');%
yl=ylabel('sin(omegat)');%
zl=zlabel('t');%
set(xl,'Rotation',30);%
set(yl,'Rotation',-30);%
grid on;
title('omega = 1rad/s Made by J Pan')
axis([-1,1,-1,1,0,4*pi])
N = 200;
t=linspace(0,4*pi,N);
w=1;sig=-0.2;
x=exp(sig*t).*cos(w*t);
y=exp(sig*t).*sin(w*t);
a = tic; % start timer
for k = 1:N
addpoints(h,x(k),y(k),t(k));
hold on
line([0 x(k)],[0 y(k)],[t(k) t(k)],'Color','red')
b = toc(a); % check timer
if b > (1/90)
drawnow % update screen every 1/30 seconds
a = tic; % reset timer after updating
end
end
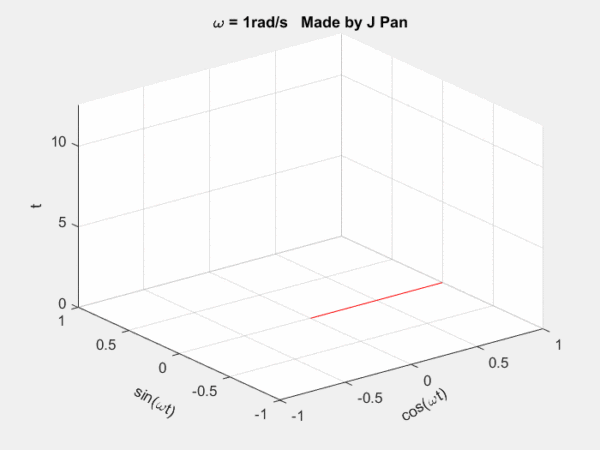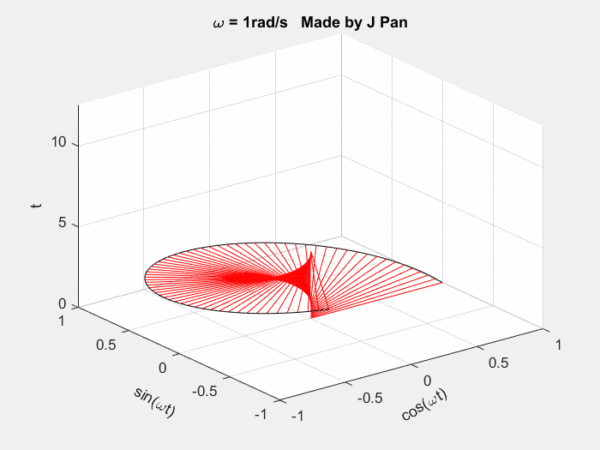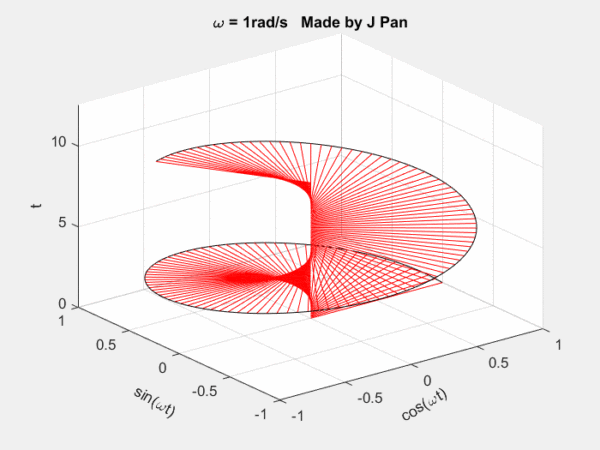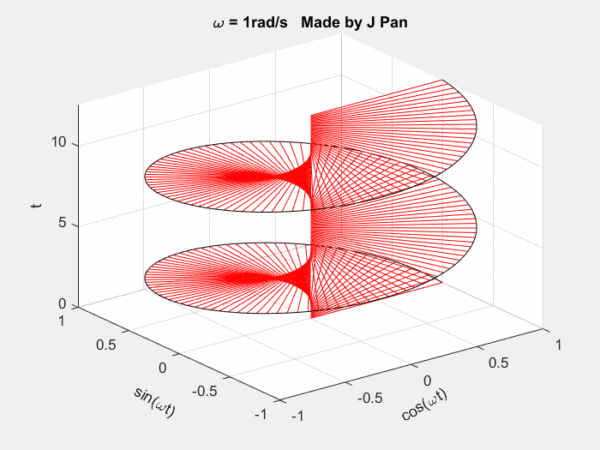
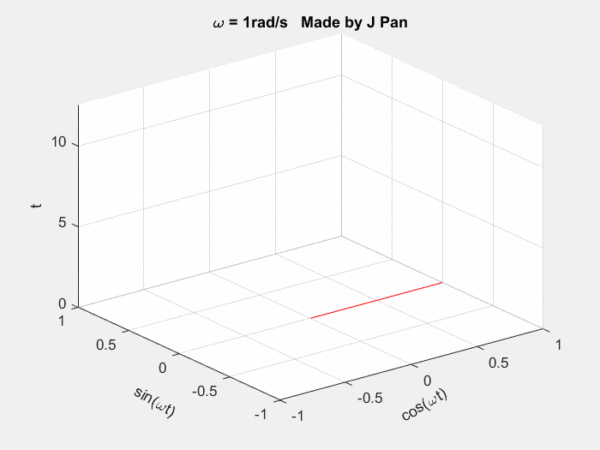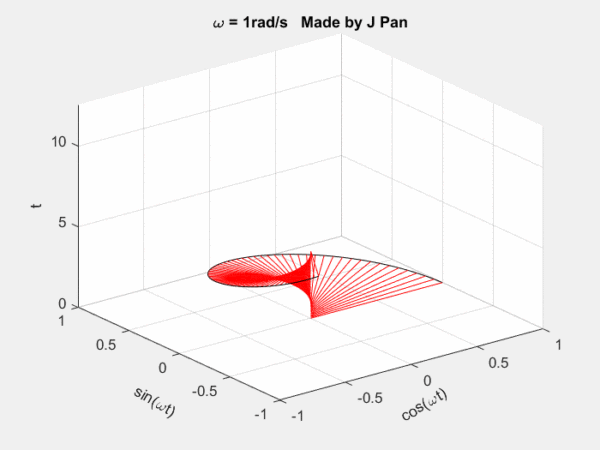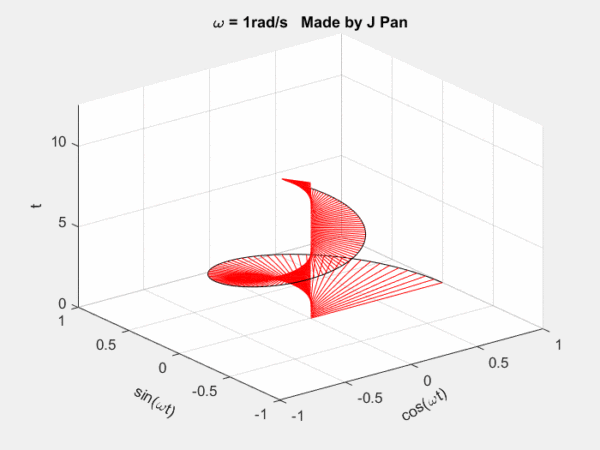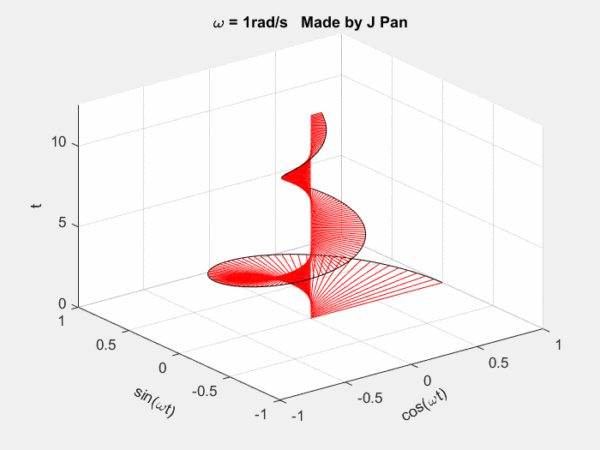
螺旋曲線和衰減函數的乘積:一個半徑不斷減小的螺旋曲線。從不同的平面看,就是不斷衰減的正弦或者余弦曲線,從復平面來看,是一個半徑不斷減小的圓。
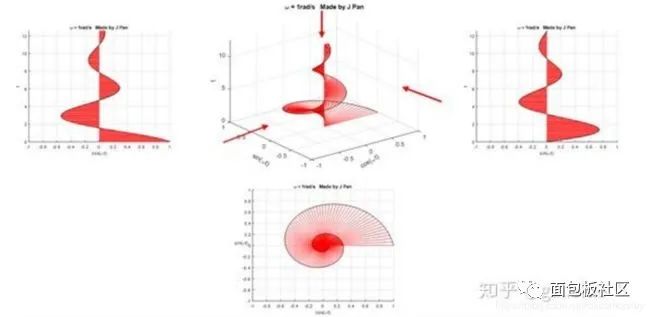
總結一下:傅里葉變換是將函數分解到頻率不同、幅值恒為1的單位圓上;拉普拉斯變換是將函數分解到頻率幅值都在變化的圓上。因為拉普拉斯變換的基有兩個變量,因此更靈活,適用范圍更廣。
審核編輯 :李倩
-
拉普拉斯
+關注
關注
0文章
35瀏覽量
9666 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42636
原文標題:拉普拉斯變換的本質意義(通俗易懂的好文)
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
拉普拉斯、傅里葉及各種變換的原理和意義
拉普拉斯變換及其逆變換表拉普拉斯變換及其逆變換表





 拉普拉斯變換的本質意義
拉普拉斯變換的本質意義
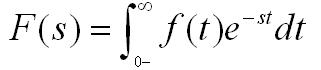










評論