轉眼間已到了畢業第八個年頭,一直在學習、一直在鉆研、也一直在成長,只因這是自己喜歡的工作。以技術立身,累并快樂著。
最近一段時間因為工作需要開始研究SVPWM調制,有了一些心得給大家分享。SVPWM比較難以理解,個人認為公式的推導過程是理解SVPWM的關鍵,扇區分配一定要親自去畫矢量圖,對理解很有幫助。
1、旋轉矢量的合成
為什么要進行矢量合成?正常來說三相就應該控制三個量,三個量很難控制,但是三個量之間存在關系,所以我們可以把它們合成一個量控制。
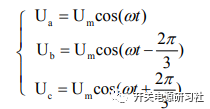
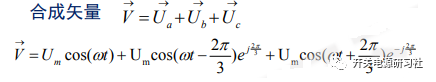
根據歐拉公式: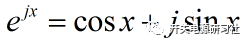 帶入上式得
帶入上式得
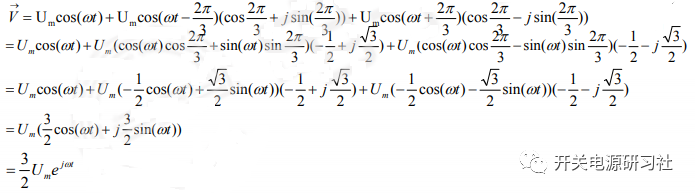
這個公式會在各種相關論文上重復出現。三相合成矢量角速度為wt,幅值為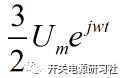 .
.
2、Clark變換與Park變換
逆變器三相輸出電壓為:
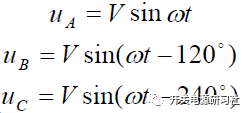
將上面式子展開可以得到:
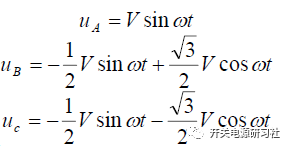
如果是在靜止坐標系的情況下,那么在中間旋轉的電壓矢量V在靜止坐標系αβ 里面的投影分別為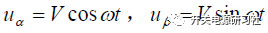 ,
,
進行矩陣變換:
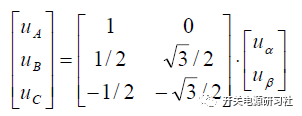
進行矩陣逆變換:
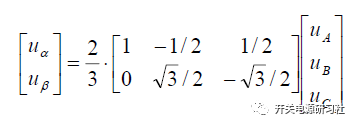
將dq 旋轉坐標系轉換到靜止坐標系αβ 之中:
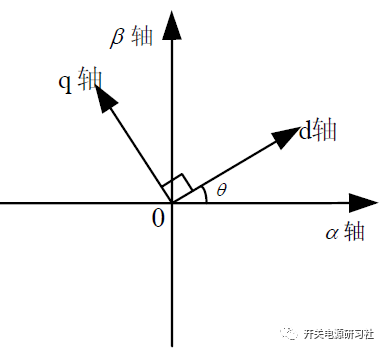
在兩相旋轉坐標系的情況下,中間旋轉的電壓矢量V在兩相同步旋轉坐標系dq 里面的投影分別為:
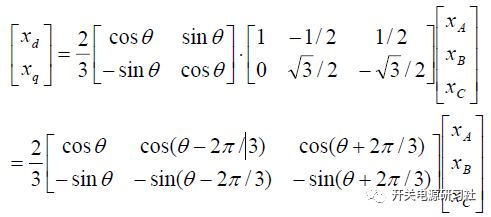
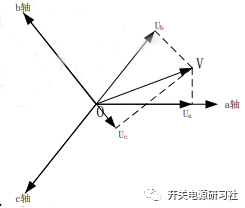
空間電壓矢量V的頂點的軌跡是一個圓,圓相應的半徑為相電壓幅值的1.5 倍。那么空間電壓矢量的軌跡越接近圓,也就意味著三相輸出相電壓越接近于三相對稱正弦波,所以使逆變器輸出的空間電壓矢量頂點的運動軌跡越接近一個標準圓,輸出相電壓的波形也就越好。通過空間矢量變換,使三個標量的控制問題轉化成了一個矢量的控制問題。
3、扇區劃分
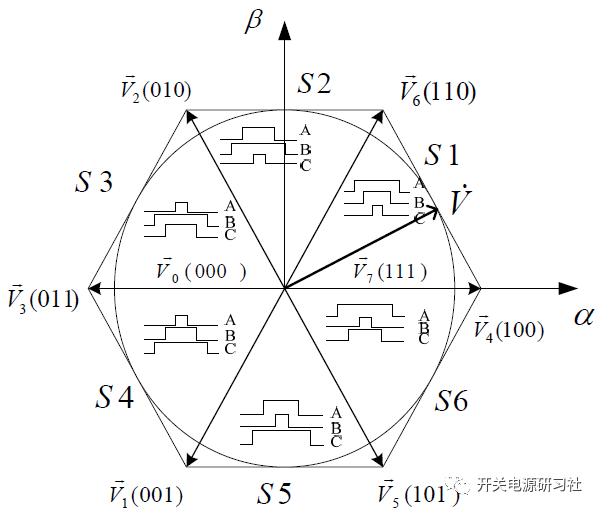
先來看第一扇區滿足的條件,首先是在第一象限,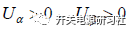 ,其次
,其次
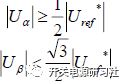
其中 ,進一步簡化關系,這個公式可以簡化成,
,進一步簡化關系,這個公式可以簡化成,
其它扇區依此類推,可以得到相應關系如下:
在第二扇區的時候:
在第三扇區的時候:
在第四扇區的時候:
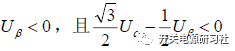
在第五扇區的時候:
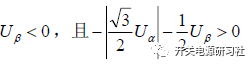
在第六扇區的時候:
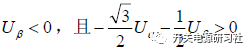
分析上面的結果,可以很明顯的看出來,如果想知道在哪個扇區,我們完全可以根據上面三個式子與零的關系來推理得到。
如果他們大于零的話,用1來表示,小于零的話用0來表示。并且用A、B、C 來對應相應的邏輯值,即如下所示:
如果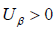 ,那么A =1,否則A = 0
,那么A =1,否則A = 0
如果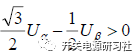 ,那么B = 1,否則B = 0
,那么B = 1,否則B = 0
如果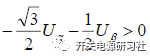 ,那么C = 1,否則C = 0
,那么C = 1,否則C = 0
令N = A + 2B + 4C,這個也好理解,對應著二進制001、010、100,
這樣每一個N 就對應著一個扇區,計算出相應結果,對應的表格如下所示:

這種方法判斷扇區比較簡單,具體分配扇區的時候將計算出來的N 值與實際扇區號對應起來就可以了。
4、扇區矢量時間計算
以第一扇區為例:
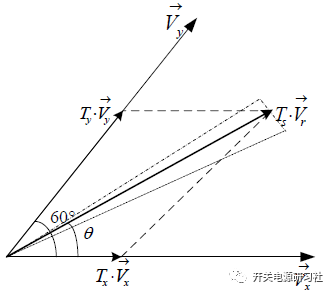
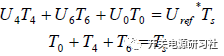
用αβ 坐標系來描述上面的公式,那么可以得到:
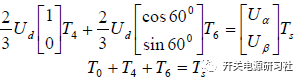
解出上面的關系式可以得到:
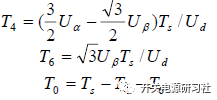
用同樣的方法可以得到在其它扇區各個適量的作用時間:

我們定義:
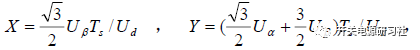
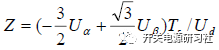
那么相關的賦值可以單獨算出 X,Y,Z 既可,然后給他們分配給相應的扇區。時間分配就變為:

最終得到每個采樣周期中各矢量切換點的數值,將他們與一定頻率和幅度的三角載波進行相應的比較,這樣就完成了SVPWM變換。
審核編輯:何安
-
調制
+關注
關注
0文章
157瀏覽量
29664 -
PWM
+關注
關注
114文章
5181瀏覽量
213799
原文標題:SVPWM三相調制
文章出處:【微信號:gh_c09253ac0c9c,微信公眾號:開關電源研習社】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
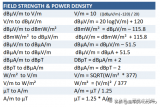
EMC常見公式大全
云端彈性計算公式有哪些內容?
buck電路穩態電壓推導過程
級聯噪聲系數公式的推導
神經網絡反向傳播算法的推導過程
半導體器件基礎公式全解析:為高性能器件設計鋪路





 公式推導過程是理解SVPWM的關鍵
公式推導過程是理解SVPWM的關鍵











評論