之前經常講涉及遞歸的算法題，我說過寫遞歸算法的一個技巧就是不要試圖跳進遞歸細節，而是從遞歸框架上思考，從函數定義去理解遞歸函數到底該怎么實現。

而且我們前文學習數據結構和算法的框架思維特別強調過，練習遞歸的框架思維最好方式就是從二叉樹相關題目開始刷，前文也有好幾篇手把手帶你刷二叉樹和二叉搜索樹的文章：

• 手把手帶你刷二叉樹（第一期）

• 手把手帶你刷二叉樹（第二期）

• 手把手帶你刷二叉樹（第三期）

• 手把手帶你刷二叉搜索樹（第一期）

• 手把手帶你刷二叉搜索樹（第二期）

• 手把手帶你刷二叉搜索樹（第三期）

之前的文章全部都是運用二叉樹的遞歸框架，幫你透過現象看本質，明白二叉樹的各種題目本質都是前中后序遍歷衍生出來的。

前文BFS 算法框架詳解是利用隊列迭代地遍歷二叉樹，不過使用的是層級遍歷，沒有遞歸遍歷中的前中后序之分。

由于現在面試越來越卷，很多讀者在后臺問我如何將前中后序的遞歸框架改寫成迭代形式。

首先我想說，遞歸改迭代從實用性的角度講是沒什么意義的，明明可以寫遞歸解法，為什么非要改成迭代的方式？

對于二叉樹來說，遞歸解法是最容易理解的，非要讓你改成迭代，頂多是考察你對遞歸和棧的理解程度，架不住大家問，那就總結一下吧。

我以前見過一些迭代實現二叉樹前中后序遍歷的代碼模板，比較短小，容易記，但通用性較差。

通用性較差的意思是說，模板只是針對「用迭代的方式返回二叉樹前/中/后序的遍歷結果」這個問題，函數簽名類似這樣，返回一個TreeNode列表：

Listtraverse(TreeNoderoot);

如果給一些稍微復雜的二叉樹問題，比如最近公共祖先，二叉搜索子樹的最大鍵值和，想把這些遞歸解法改成迭代，就無能為力了。

而我想要的是一個萬能的模板，可以把一切二叉樹遞歸算法都改成迭代。

換句話說，類似二叉樹的遞歸框架：

voidtraverse(TreeNoderoot){
if(root==null)return;
/*前序遍歷代碼位置*/
traverse(root.left);
/*中序遍歷代碼位置*/
traverse(root.right);
/*后序遍歷代碼位置*/
}

迭代框架也應該有前中后序代碼的位置：

voidtraverse(TreeNoderoot){
while(...){
if(...){
/*前序遍歷代碼位置*/
}
if(...){
/*中序遍歷代碼位置*/
}
if(...){
/*后序遍歷代碼位置*/
}
}
}

我如果想把任何一道二叉樹遞歸解法改成迭代，直接把遞歸解法中前中后序對應位置的代碼復制粘貼到迭代框架里，就可以直接運行，得到正確的結果。

理論上，所有遞歸算法都可以利用棧改成迭代的形式，因為計算機本質上就是借助棧來迭代地執行遞歸函數的。

所以本文就來利用「棧」模擬函數遞歸的過程，總結一套二叉樹通用迭代遍歷框架。

遞歸框架改為迭代

參加過我的二叉樹專項訓練的讀者應該知道，二叉樹的遞歸框架中，前中后序遍歷位置就是幾個特殊的時間點：

前序遍歷位置的代碼，會在剛遍歷到當前節點root，遍歷root的左右子樹之前執行；

中序遍歷位置的代碼，會在在遍歷完當前節點root的左子樹，即將開始遍歷root的右子樹的時候執行；

后序遍歷位置的代碼，會在遍歷完以當前節點root為根的整棵子樹之后執行。

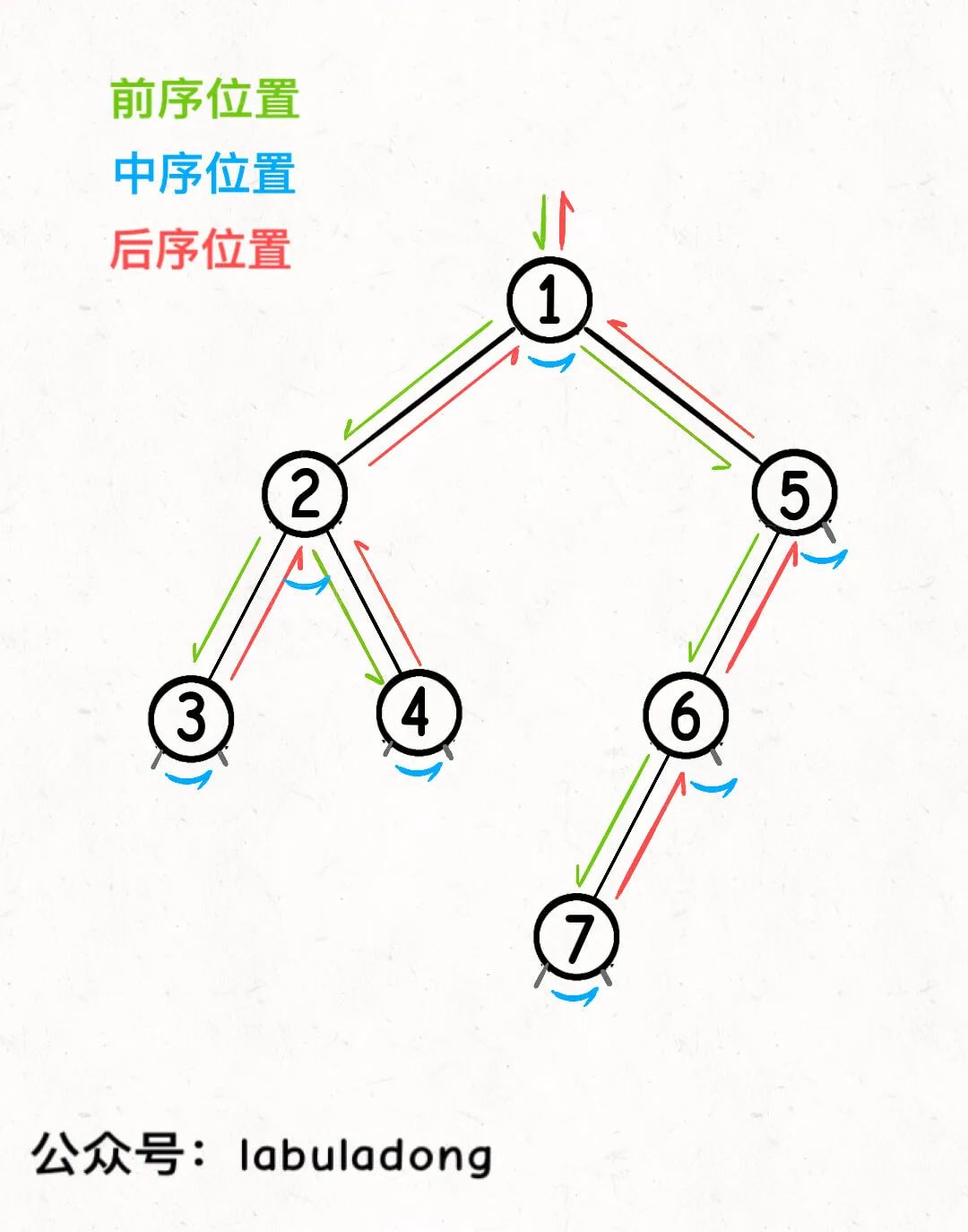
如果從遞歸代碼上來看，上述結論是很容易理解的：

voidtraverse(TreeNoderoot){
if(root==null)return;
/*前序遍歷代碼位置*/
traverse(root.left);
/*中序遍歷代碼位置*/
traverse(root.right);
/*后序遍歷代碼位置*/
}

不過，如果我們想將遞歸算法改為迭代算法，就不能從框架上理解算法的邏輯，而要深入細節，思考計算機是如何進行遞歸的。

假設計算機運行函數A，就會把A放到調用棧里面，如果A又調用了函數B，則把B壓在A上面，如果B又調用了C，那就再把C壓到B上面……

當C執行結束后，C出棧，返回值傳給B，B執行完后出棧，返回值傳給A，最后等A執行完，返回結果并出棧，此時調用棧為空，整個函數調用鏈結束。

我們遞歸遍歷二叉樹的函數也是一樣的，當函數被調用時，被壓入調用棧，當函數結束時，從調用棧中彈出。

那么我們可以寫出下面這段代碼模擬遞歸調用的過程：

//模擬系統的函數調用棧
Stackstk=newStack<>();

voidtraverse(TreeNoderoot){
if(root==null)return;
//函數開始時壓入調用棧
stk.push(root);
traverse(root.left);
traverse(root.right);
//函數結束時離開調用棧
stk.pop();
}

如果在前序遍歷的位置入棧，后序遍歷的位置出棧，stk中的節點變化情況就反映了traverse函數的遞歸過程（綠色節點就是被壓入棧中的節點，灰色節點就是彈出棧的節點）：

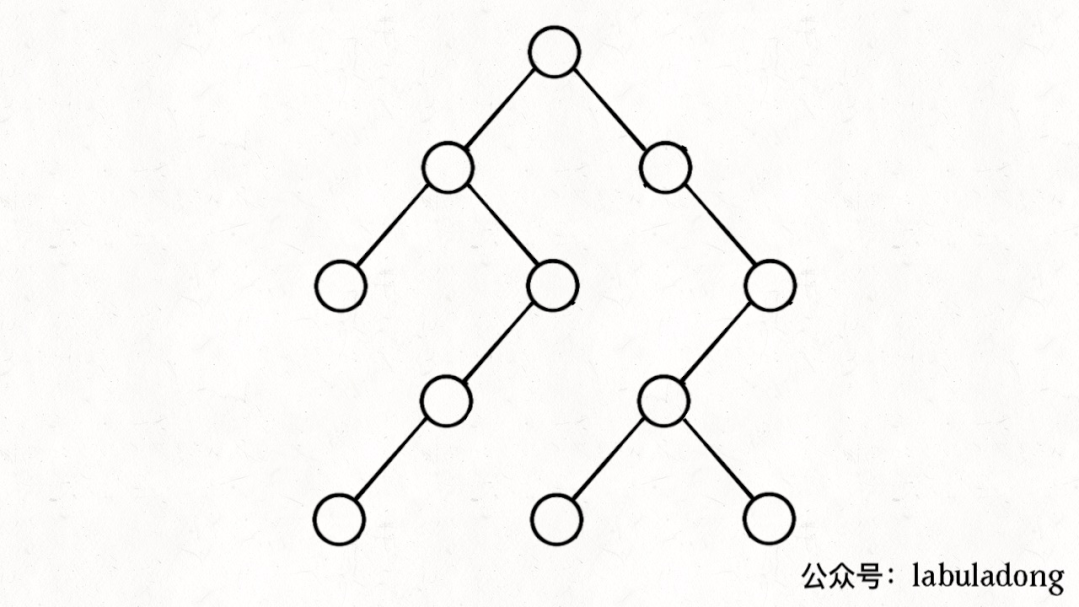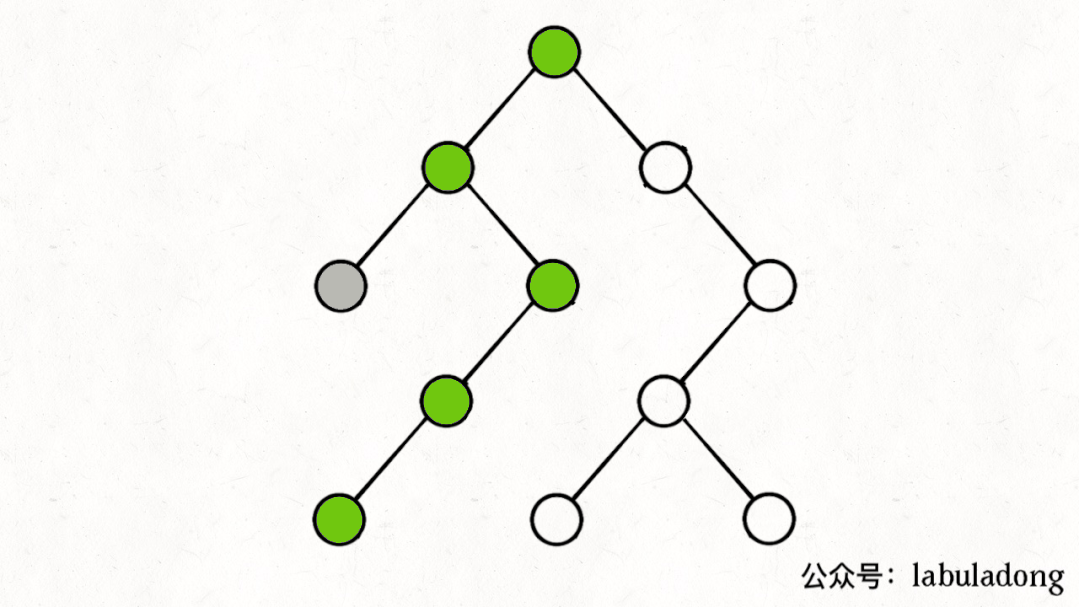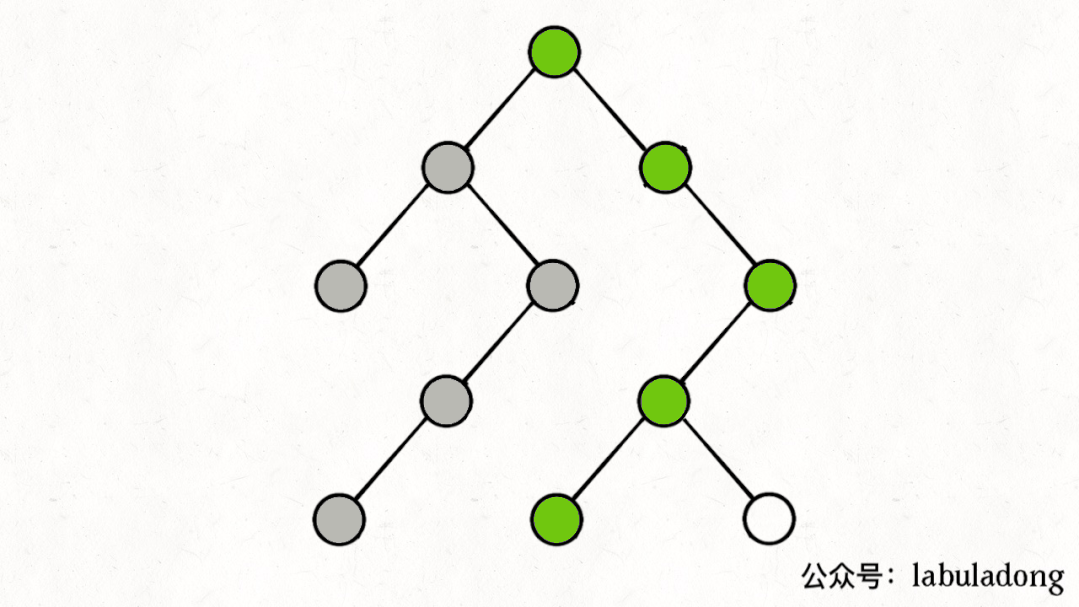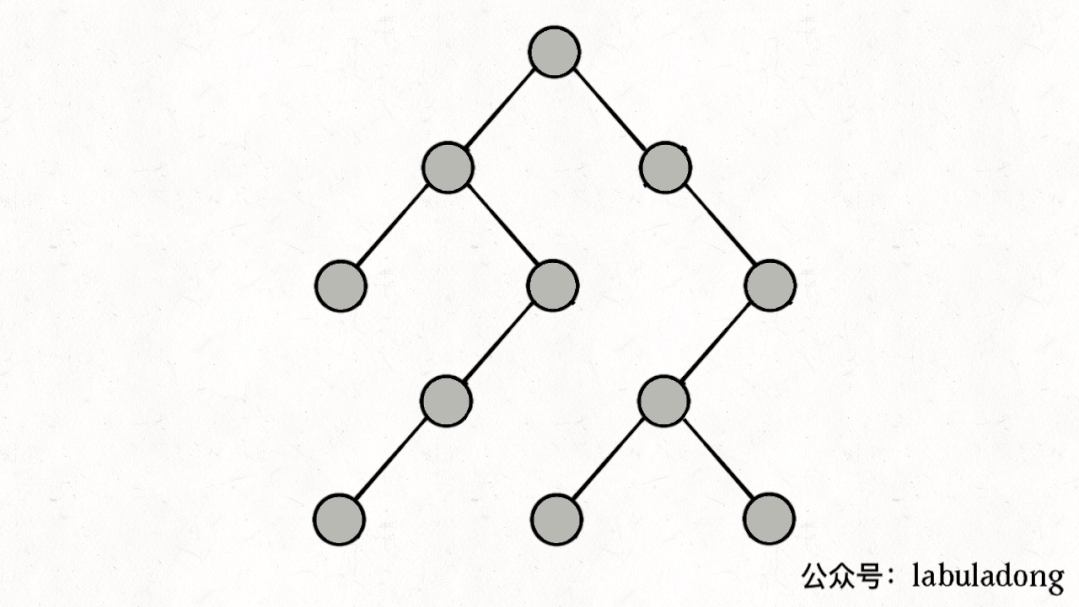
簡單說就是這樣一個流程：

1、拿到一個節點，就一路向左遍歷（因為traverse(root.left)排在前面），把路上的節點都壓到棧里。

2、往左走到頭之后就開始退棧，看看棧頂節點的右指針，非空的話就重復第 1 步。

寫成迭代代碼就是這樣：

privateStackstk=newStack<>();

publicListtraverse(TreeNoderoot){
pushLeftBranch(root);

while(!stk.isEmpty()){
TreeNodep=stk.pop();
pushLeftBranch(p.right);
}
}

//左側樹枝一擼到底，都放入棧中
privatevoidpushLeftBranch(TreeNodep){
while(p!=null){
stk.push(p);
p=p.left;
}
}

上述代碼雖然已經可以模擬出遞歸函數的運行過程，不過還沒有找到遞歸代碼中的前中后序代碼位置，所以需要進一步修改。

迭代代碼框架

想在迭代代碼中體現前中后序遍歷，關鍵點在哪里？

當我從棧中拿出一個節點p，我應該想辦法搞清楚這個節點p左右子樹的遍歷情況。

如果p的左右子樹都沒有被遍歷，那么現在對p進行操作就屬于前序遍歷代碼。

如果p的左子樹被遍歷過了，而右子樹沒有被遍歷過，那么現在對p進行操作就屬于中序遍歷代碼。

如果p的左右子樹都被遍歷過了，那么現在對p進行操作就屬于后序遍歷代碼。

上述邏輯寫成偽碼如下：

privateStackstk=newStack<>();

publicListtraverse(TreeNoderoot){
pushLeftBranch(root);

while(!stk.isEmpty()){
TreeNodep=stk.peek();

if(p的左子樹被遍歷完了){
/*******************/
/**中序遍歷代碼位置**/
/*******************/
//去遍歷p的右子樹
pushLeftBranch(p.right);
}

if(p的右子樹被遍歷完了){
/*******************/
/**后序遍歷代碼位置**/
/*******************/
//以p為根的樹遍歷完了，出棧
stk.pop();
}
}
}

privatevoidpushLeftBranch(TreeNodep){
while(p!=null){
/*******************/
/**前序遍歷代碼位置**/
/*******************/
stk.push(p);
p=p.left;
}
}

有剛才的鋪墊，這段代碼應該是不難理解的，關鍵是如何判斷p的左右子樹到底被遍歷過沒有呢？

其實很簡單，我們只需要維護一個visited指針，指向「上一次遍歷完成的根節點」，就可以判斷p的左右子樹遍歷情況了

下面是迭代遍歷二叉樹的完整代碼框架：

//模擬函數調用棧
privateStackstk=newStack<>();

//左側樹枝一擼到底
privatevoidpushLeftBranch(TreeNodep){
while(p!=null){
/*******************/
/**前序遍歷代碼位置**/
/*******************/
stk.push(p);
p=p.left;
}
}

publicListtraverse(TreeNoderoot){
//指向上一次遍歷完的子樹根節點
TreeNodevisited=newTreeNode(-1);
//開始遍歷整棵樹
pushLeftBranch(root);

while(!stk.isEmpty()){
TreeNodep=stk.peek();

//p的左子樹被遍歷完了，且右子樹沒有被遍歷過
if((p.left==null||p.left==visited)
&&p.right!=visited){
/*******************/
/**中序遍歷代碼位置**/
/*******************/
//去遍歷p的右子樹
pushLeftBranch(p.right);
}
//p的右子樹被遍歷完了
if(p.right==null||p.right==visited){
/*******************/
/**后序遍歷代碼位置**/
/*******************/
//以p為根的子樹被遍歷完了，出棧
//visited指針指向p
visited=stk.pop();
}
}
}

代碼中最有技巧性的是這個visited指針，它記錄最近一次遍歷完的子樹根節點（最近一次pop出棧的節點），我們可以根據對比p的左右指針和visited是否相同來判斷節點p的左右子樹是否被遍歷過，進而分離出前中后序的代碼位置。

PS：visited指針初始化指向一個新 new 出來的二叉樹節點，相當于一個特殊值，目的是避免和輸入二叉樹中的節點重復。

只需把遞歸算法中的前中后序位置的代碼復制粘貼到上述框架的對應位置，就可以把任意遞歸的二叉樹算法改寫成迭代形式了。

比如，讓你返回二叉樹后序遍歷的結果，你就可以這樣寫：

privateStackstk=newStack<>();

publicListpostorderTraversal(TreeNoderoot){
//記錄后序遍歷的結果
Listpostorder=newArrayList<>();
TreeNodevisited=newTreeNode(-1);

pushLeftBranch(root);
while(!stk.isEmpty()){
TreeNodep=stk.peek();

if((p.left==null||p.left==visited)
&&p.right!=visited){
pushLeftBranch(p.right);
}

if(p.right==null||p.right==visited){
//后序遍歷代碼位置
postorder.add(p.val);
visited=stk.pop();
}
}

returnpostorder;
}

privatevoidpushLeftBranch(TreeNodep){
while(p!=null){
stk.push(p);
p=p.left;
}
}

當然，任何一個二叉樹的算法，如果你想把遞歸改成迭代，都可以套用這個框架，只要把遞歸的前中后序位置的代碼對應過來就行了。

迭代解法到這里就搞定了，不過我還是想強調，除了 BFS 層級遍歷之外，二叉樹的題目還是用遞歸的方式來做，因為遞歸是最符合二叉樹結構特點的。

說到底，這個迭代解法就是在用棧模擬遞歸調用，所以對照著遞歸解法，應該不難理解和記憶。