理論力學、材料力學與結構力學合稱“工程力學”,是工程學科力學基礎中的三門主要學科。
理論力學的研究內容包括靜力學、運動學與動力學,有很多內容與《物理學》中的力學部分相重復,當然也有深化的內容。在工程學科中,尤其在建筑結構設計中,其靜力學部分用到的更多一些。
實際上,在機械工程與航空航天工程中,運動學是很重要的一個內容。以機械工程為例,機構的設計首先需要分析其運動狀態,求出各組成部分的速度與加速度,然后才能借助動力學方程進行力的分析,其中當然離不開靜力學知識。在流體力學中也是如此,以壓力管道彎頭鎮墩計算為例,在分析其受力狀態時,需要利用動力學中的動量方程來計算水的沖擊力。
所以,在建筑結構中,相對而言其靜力學部分的應用更多一些。動力學計算中的擬靜力法(如抗震計算中基于反應譜理論的方法),實際上源自于理論力學中的達朗貝爾原理(亦稱動靜法,就是把動力學問題轉化為靜力學問題來處理)。可以說,理論力學是力學學科群的基礎,在材料力學、結構力學,乃至彈塑性力學等等,都涉及到力的平衡關系,而這正是靜力學研究的內容。
材料力學研究桿件的受力與變形,其基本變形包括軸向拉壓、剪切、扭轉與彎曲,更復雜的變形無非是這些基本變形的組合而已(如壓桿穩定就是彎曲與軸向受壓的組合),與之相應的內力包括軸力、剪力、扭矩與彎矩。從微觀角度看,基本變形可歸結為正應變與切應變,基本內力可歸結為正應力與切應力,而聯系應力與應變的橋梁就是胡克定律。
材料力學的研究方法從宏觀上看就是取隔離體,然后研究力的平衡關系。其中用到三個基本方程:靜力平衡方程、幾何方程和物理方程。靜力平衡方程是理論力學中靜力學的內容;幾何方程是桿件變形后基本尺寸之間空間關系的度量;物理方程也稱本構方程,就是描述應力與應變之間的關系,也即上述胡克定律(考慮復雜應力狀態時也就是廣義胡克定律)。當然在上述研究過程中需要幾個基本假定:線彈性、連續均勻、各向同性及小變形。若超過一定限度,就會產生很大的誤差,此時需要用彈塑性力學、斷裂損傷力學等進行研究。
在材料力學中,還會研究截面的一些幾何性質:面積、靜矩、慣性矩、慣性積、極慣性矩、慣性半徑,等等。既然是幾何性質,那就純粹是一個數學問題,實際上大多也是用積分的方法進行計算的。這里并不存在大的難度,只是如組合截面等其計算繁瑣一些而已。
結構力學研究桿系結構的受力與變形問題,研究的是具體的實用的結構,如框架、排架、拱、桁架等結構。桿系結構是由桿件組成的,拆開來就是一根根桿件。所以結構力學的基礎是材料力學,因為說到底其基本變形與內力完全與材料力學研究的相同。由于組成了桿件體系,所以就有不同的研究方法。
其基本的方法就是力法與位移法,從實用性出發,又衍生出一些迭代解法,如彎矩(力矩)分配法,剪力分配法,框架結構分析中的反彎點法與D值法,拱結構分析中的彈性中心法,等等。進一步離散后,就是矩陣位移法,再進一步延伸與擴展到目前應用廣泛的有限元法,只不過一個只適用于桿件結構(又可稱作“桿件結構有限元分析”),一個更適用于連續介質(包括固體與流體),故其適用范圍更廣。
所以,力學的發展都是一步一步地由淺入深、由易到難、由簡到繁而來。沒有理論力學作為基礎,就無法分析結構的力學平衡關系,就無法計算出支座反力與結構內力。沒有材料力學作為鋪墊,就無法進行結構的內力與變形分析。因此,這就很難說哪個比哪個更重要,而是一個循序漸進的過程。
我覺得力學的學習與數學的學習具有可比性,不能因為高等數學的應用范圍更廣、解決問題更深入、有時甚至于更簡潔,就可以忽視初等數學的學習,因為數學中的一些基本運算法則(如結合律、交換律、分配律等),一般同樣適用于高等與初等數學,而且是在總結初等數學運算規律基礎之上得來的(當然,在高等數學中也存在如不適用交換律這樣的情況,這是與初等數學的重大區別)。因此,學科中存在的這種繼承性與擴展性,是一門學科發展中的基本的內在規律,也是其不斷走向成熟與完善的重要標志。
審核編輯 :李倩
-
結構
+關注
關注
1文章
119瀏覽量
22004 -
材料力學
+關注
關注
0文章
9瀏覽量
7662
原文標題:理論力學、材料力學與結構力學的關系
文章出處:【微信號:AMTBBS,微信公眾號:世界先進制造技術論壇】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
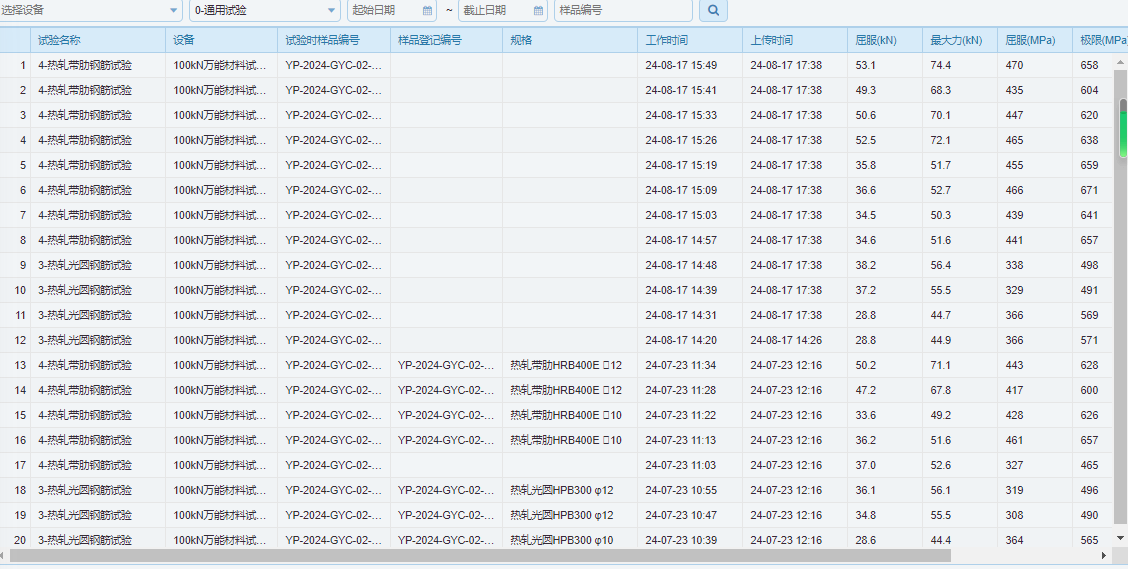
?力學試驗室數據采集系統在工程建設領域重要應用描述
《虛擬世界的力學交響曲:Adams如何重塑工業仿真邊界》
汽車物理按鍵力學檢測要點

拉力機:材料性能的 “質檢員”

Adams多體動力學仿真解決方案全面解析
輪轂電機驅動電動汽車垂向動力學控制研究綜述
航空發動機整機動力學有限元模型建立方法
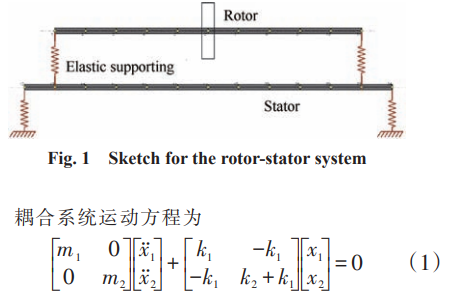
【Simcenter STAR-CCM+】通過快速準確的CFD仿真加速空氣動力學創新

使用Phase Lab鎳基動力學數據庫計算多組分合金的成分分布曲線






















評論