01 故事起源
有N個數排列成一排,給定一個區間,如何快速找出區間內最大的數是多少呢?
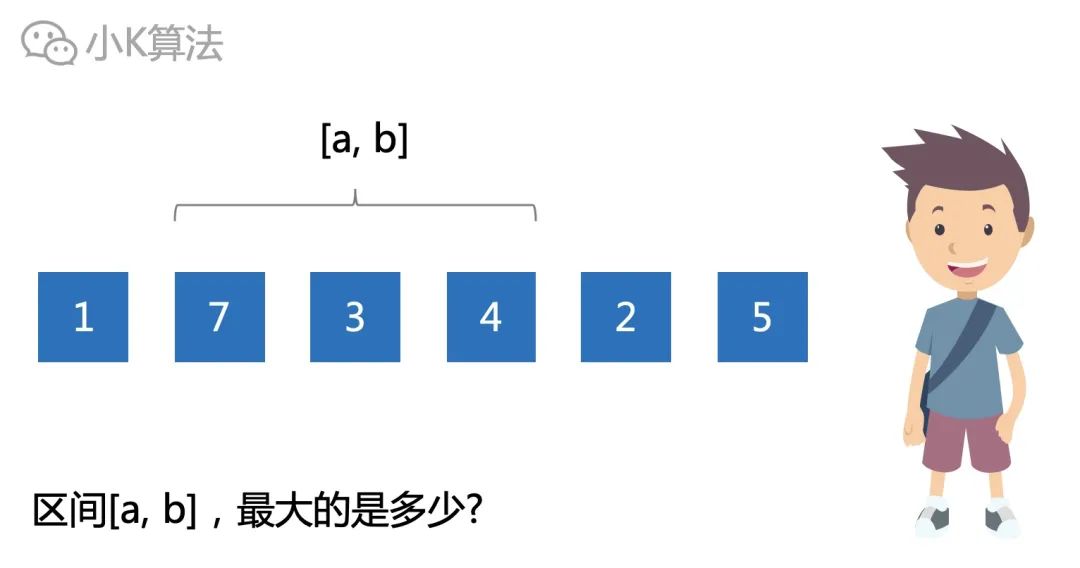
02 分析
首先想到的自然是從區間頭開始,依次遍歷完區間內的元素,這樣就可以找出結果了。但這個復雜度是O(n),肯定不是我們想要的。
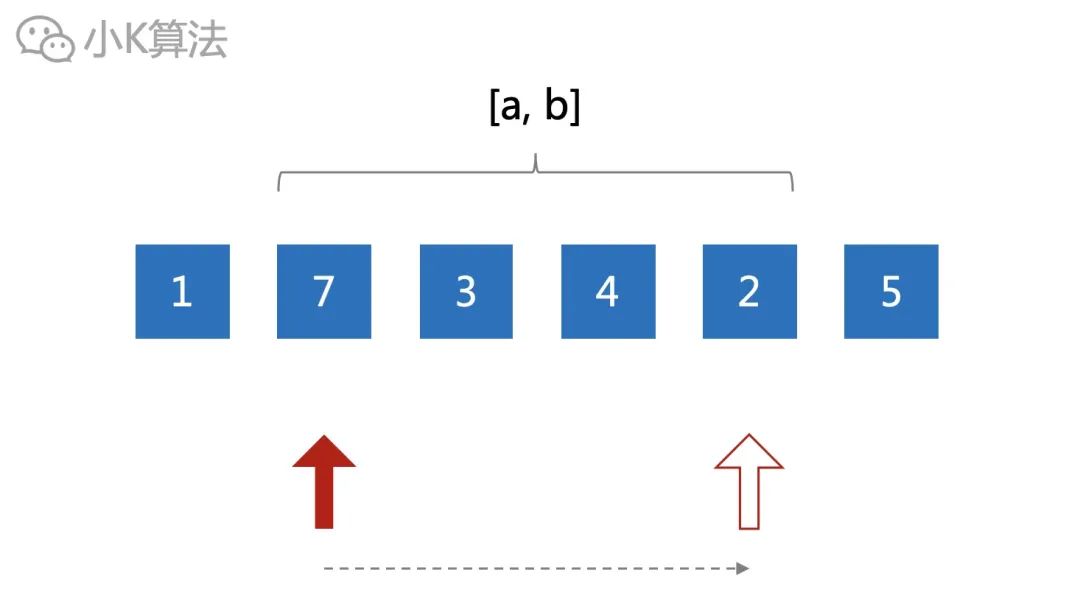
再來分析一下有什么特點呢?
這些數不會更改,所以每個區間的結果是不會變的,是否可以把所有的區間結果先計算出來?
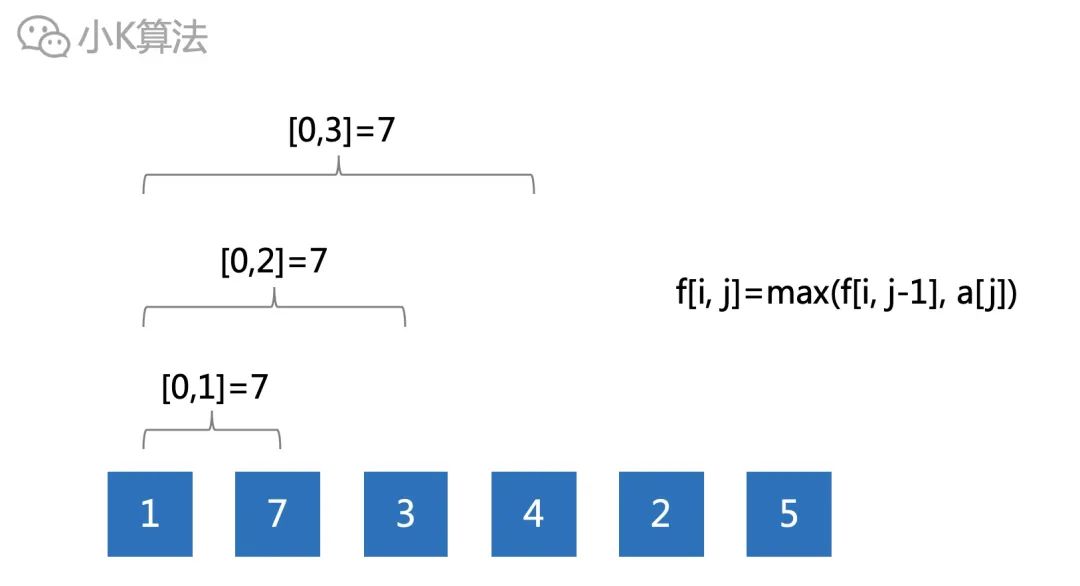
如果數據規模很小確實可以,一旦數據過大肯定就不行了,因為時間和空間都是O(n^2)。
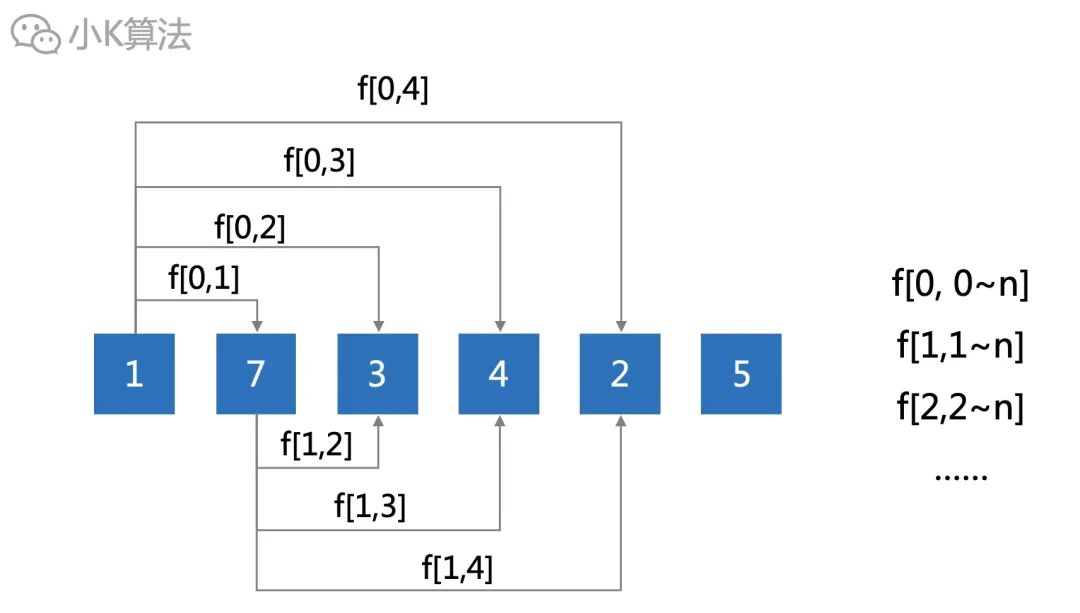
再考慮一下,區間的最值是有很強的傳遞關系,這就引導我們可以把大問題化為小問題。
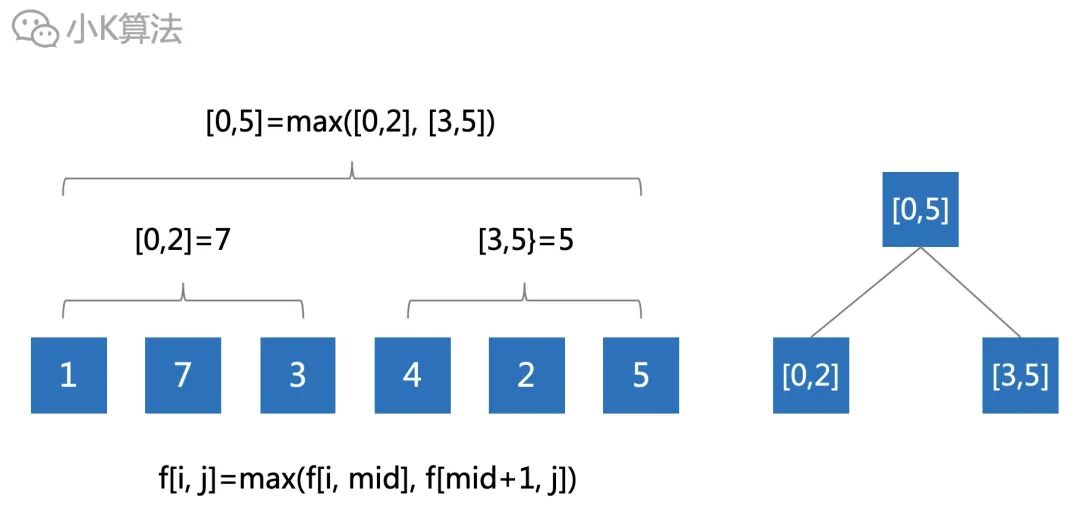
很顯然,這就是一個標準的線段樹模型,不過今天我們再換一個更加高效的算法,稀疏表。 03 稀疏表稀疏表的思想就是提前預處理數據,所以主要針對數據不變的情況,而線段樹更加靈活,可以動態維護數據的變化。
首先還是將區間劃分成很多的小區間。那如何劃分更合理?
第2章節中,我們枚舉了所有的區間情況,可以看出其實有很多重復的情況,比如下面[0,3]其實可以通過[0,1]和[2,3]組合出來。
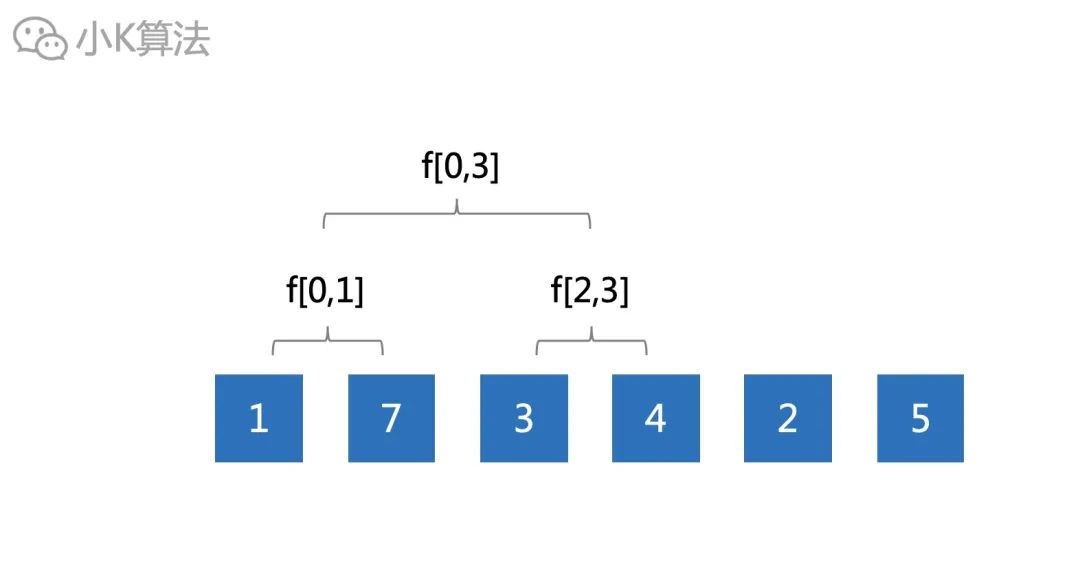
可以根據長度劃分區間。
設數組為a[i],f[i][j]表示區間[i,j]的最大值。
則長度為1的區間總共有n個,f[i][i]=a[i]。
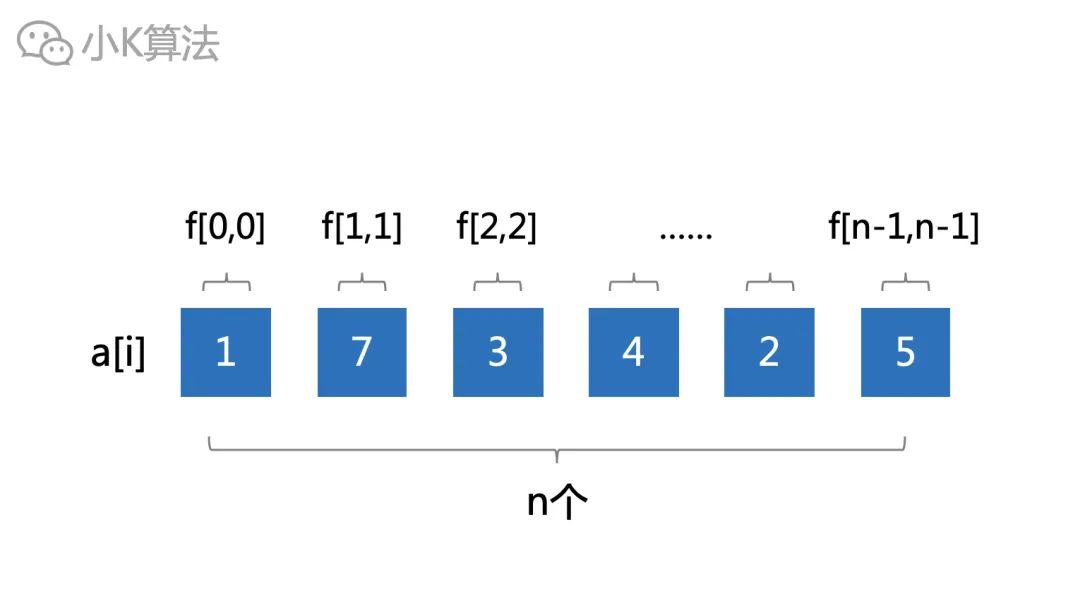
長度為2的區間總共有n-1個。
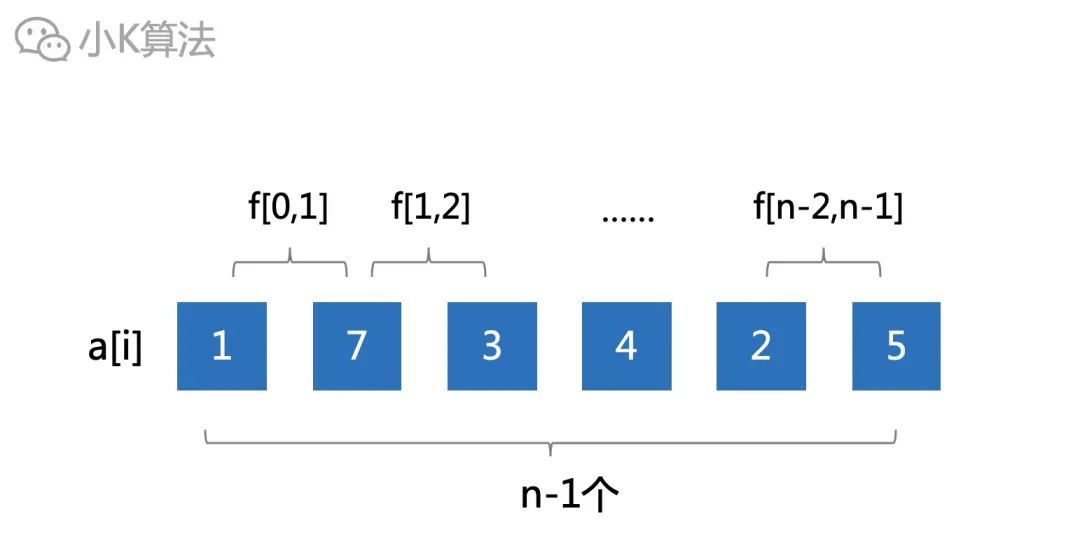
因為之前已經求出了長度為1的區間的最大值,所以區間長度為2的最大值可以通過區間長度為1的結果直接推出來。

接下來就考慮長度為3的區間了嗎?
其實并不是,因為前面已經有了長度為1和2的,所以可以組合出長度為3和4的。
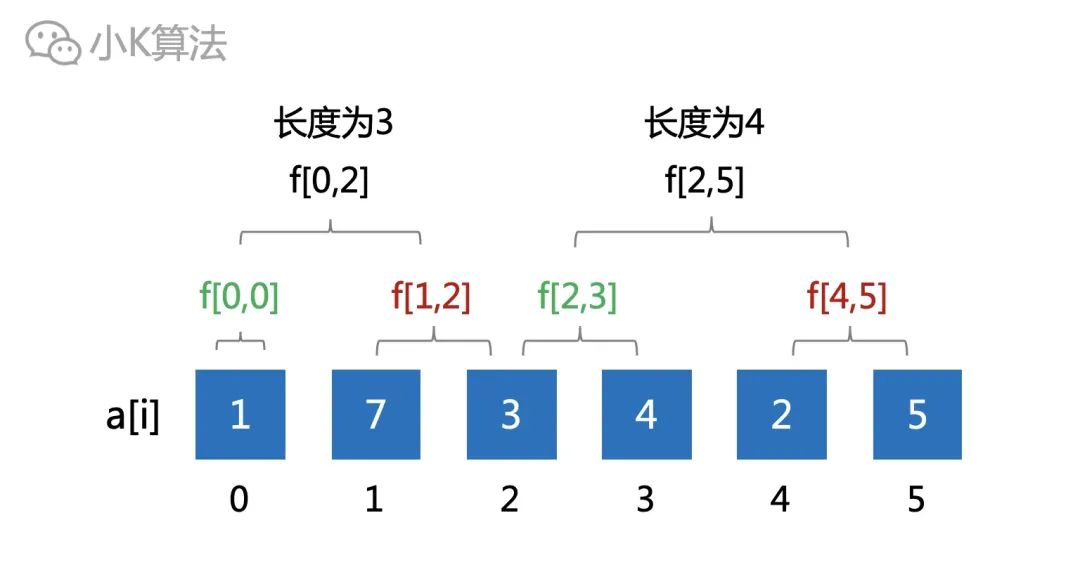
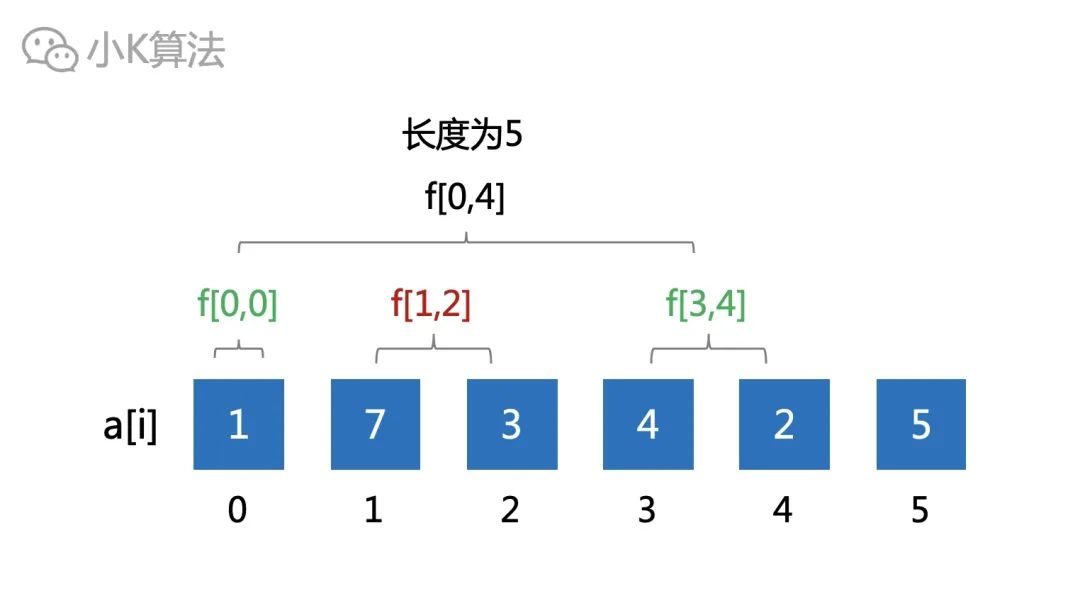
那就直接考慮長度為5的嗎?
如果考慮為5的,那你怎么計算呢,前面的也推不出長度為5的結果啊,至少得有3個區間才能推出來
。
所以接下來考慮長度為4的區間才是正解,總共有n-3個。
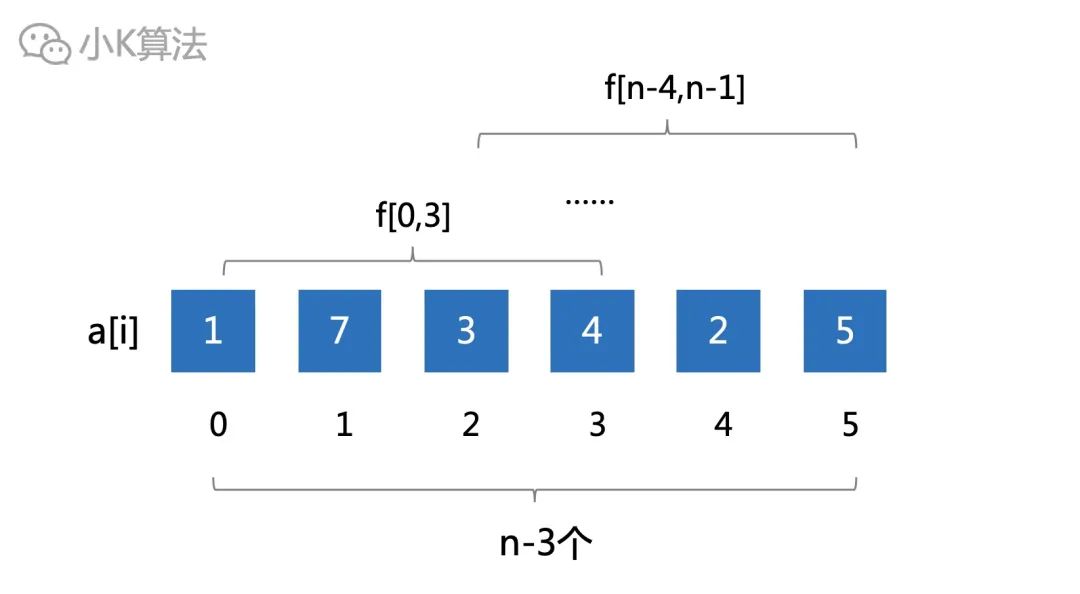
再接下來自然就是考慮長度為8的區間了,總共有n-7個。
但這里有個很明顯的問題,就是我們的數組f[i,j]定義的不合理,因為里面很多的小區間沒有用上,比如長度為3,5,6,7等,所以需要重新定義。 04 狀態壓縮可以將第二維用于表示區間長度,第一維表示區間起點,對第二維就可以進行狀態壓縮。
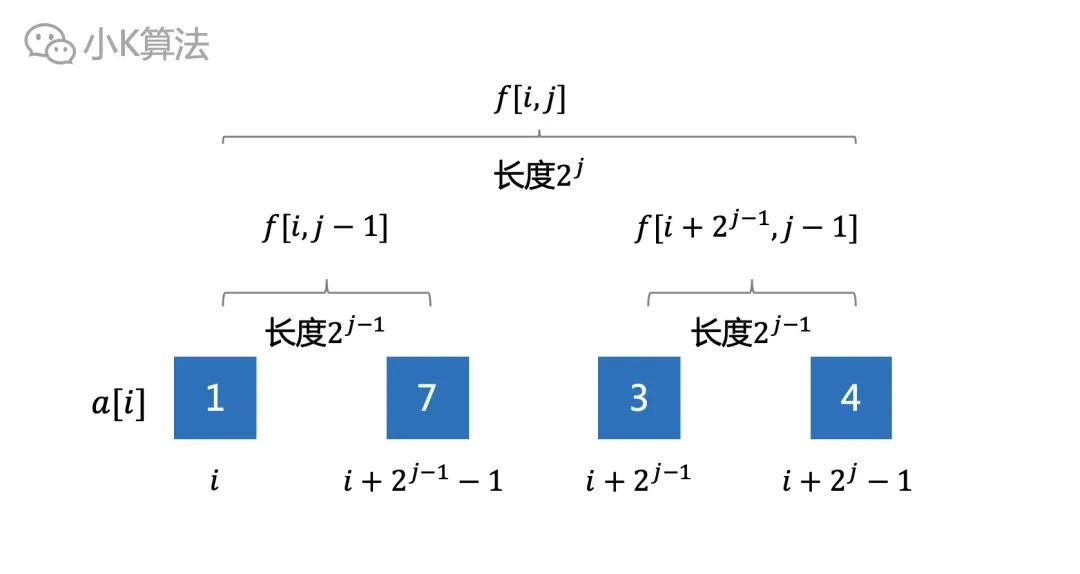
設f[i,j]表示從i開始,長度為2^j的區間的最大值,即區間[i,i+2^j-1]。
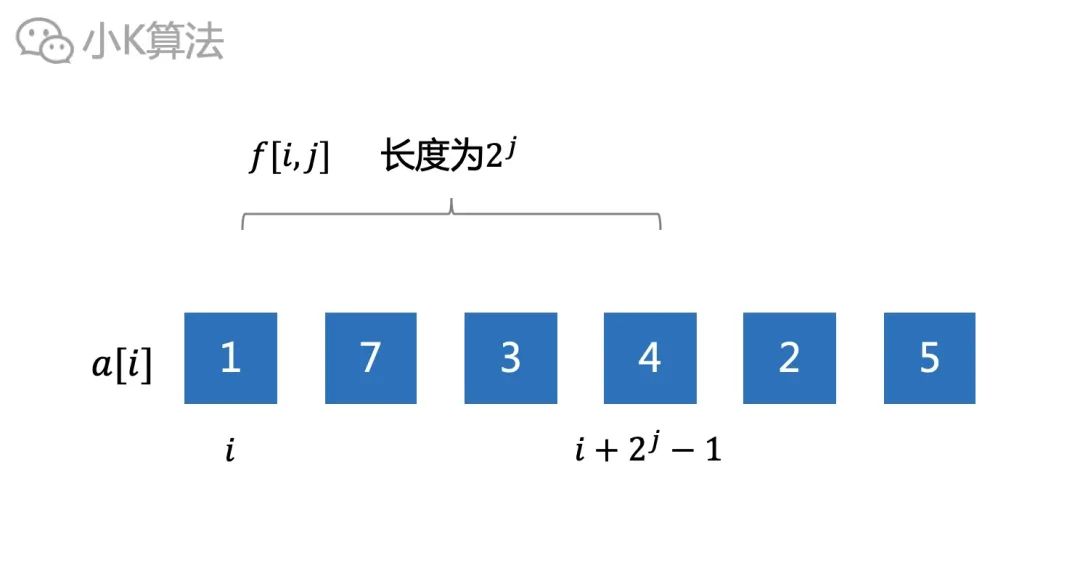
則長度為2^j的區間就可以通過左右2個長度為2^(j-1)的區間推出結果。時間和空間的復雜度都為O(nlogn)。
05 區間分解
那查詢結果的時候要怎么處理呢,我們只計算了長度為2^j的區間,并沒有計算長度為3、5、7等區間的結果。
所以這個處理和線段樹的思想也類似,需要進行區間分解。不過線段樹可能分解成很多個區間,而稀疏表只需要分解成2個區間就可以了。
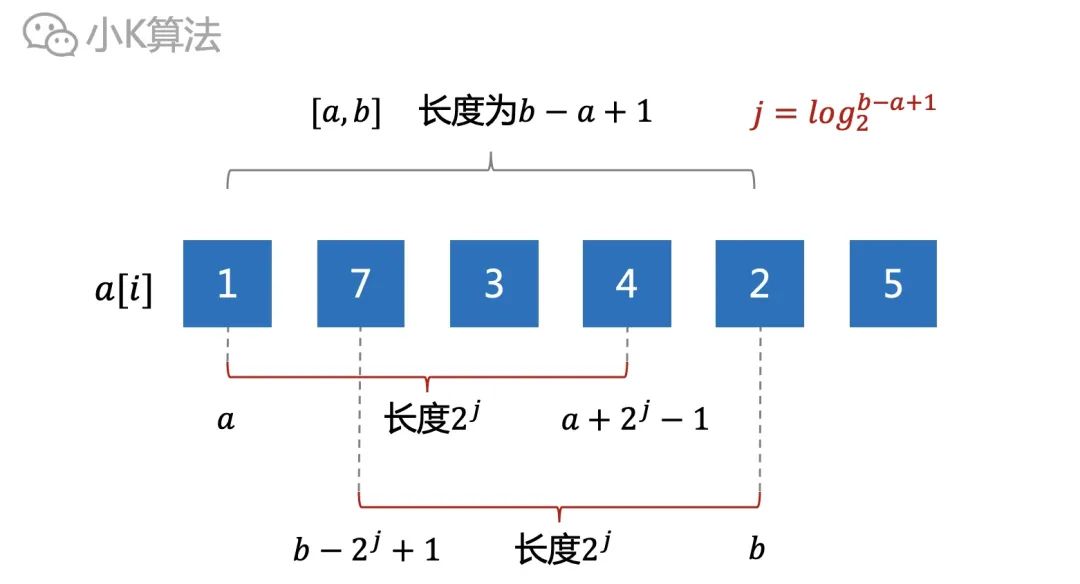
對于任意區間[a,b],長度為b-a+1,總可以找到2個長度為2^j的區間,這2個區間組合起來可以完全覆蓋[a,b],其中j的值為log(b-a+1)。
左邊的區間左端點從a開始,長度為2^j,即區間[a,a+2^j-1]。右邊的區間右端點從b開始,長度為2^j,即區間[b-2^j+1,b]。
則區間[a,b]的最大值就是這兩個區間中更大的那個,即max(f[a,j],f[b-2^j+1,j])。
06 代碼實現
代碼實現了最大值和最小值的獲取。
6.1變量定義
int high[50000][17], low[50000][17], n, q;
6.1預處理
void solve() {
// 枚舉區間長度,2^j《=n
for (int j = 1; (1 《《 j) 《= n; ++j) {
// 枚舉左端點i,右端點i+2^j-1《=n-1
for (int i = 0; i + (1 《《 j) 《= n; ++i) {
high[i][j] = max(high[i][j - 1], high[i + (1 《《 (j - 1))][j - 1]);
low[i][j] = min(low[i][j - 1], low[i + (1 《《 (j - 1))][j - 1]);
}
} }
6.1main函數
int main() {
cin 》》 n 》》 q;
for (int i = 0; i 《 n; ++i) {
cin 》》 high[i][0];
low[i][0] = high[i][0];
}
solve();
for (int i = 0; i 《 q; ++i) {
int a, b;
cin 》》 a 》》 b;
a--;
b--;
int j = (int) (log(b - a + 1.0) / log(2.0));
int minHeight = min(low[a][j], low[b - (1 《《 j) + 1][j]);
int maxHeight = max(high[a][j], high[b - (1 《《 j) + 1][j]);
cout 《《 maxHeight - minHeight 《《 endl;
}
return 0; }
07 總結
對于數據不變的情況,可以用稀疏表預處理,這種屬于離線算法。如果要動態維護變化,動態查詢,那就得用在線算法,比如線段樹。但稀疏表的效率確實高,有狀態壓縮和動態規劃的思想,值得深入研究學習。
--- EOF ---
審核編輯 :李倩
-
算法
+關注
關注
23文章
4608瀏覽量
92844 -
函數
+關注
關注
3文章
4329瀏覽量
62575
原文標題:一種比線段樹還高效的區間算法
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
一種混合顏料光譜分區間識別方法
【「從算法到電路—數字芯片算法的電路實現」閱讀體驗】+一本介紹基礎硬件算法模塊實現的好書
華納云:Chord算法如何管理節點間的聯系?
一種基于深度學習的二維拉曼光譜算法

Huffman壓縮算法概述和詳細流程
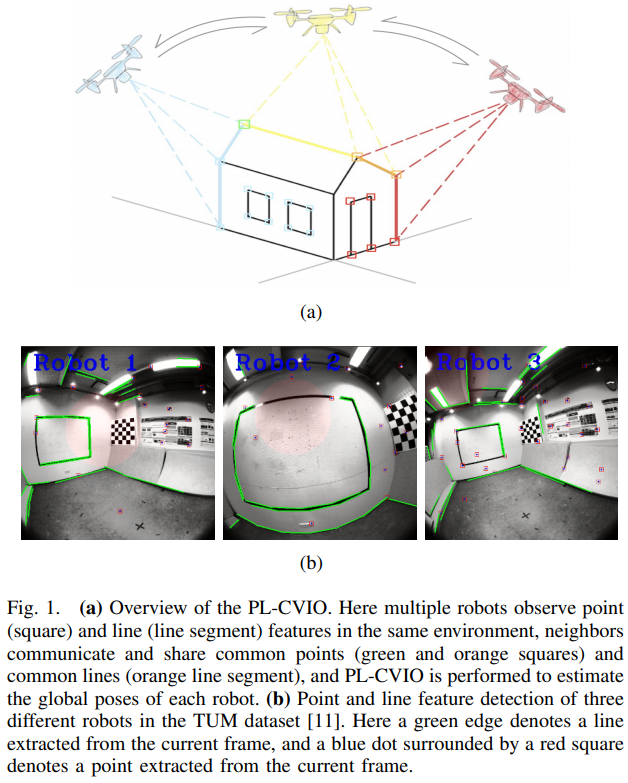
一種完全分布式的點線協同視覺慣性導航系統




 一種比線段樹還高效的區間算法
一種比線段樹還高效的區間算法










評論