在第一篇文章 時空藍色噪聲實時渲染,第 1 部分 中,我們將時間軸和重要性采樣引入藍色噪波紋理。在這篇文章中,我們將深入了解,展示一些擴展,并解釋一些最佳實踐。
藍色噪音是如何工作的,為什么?
藍色噪波紋理中的相鄰像素彼此具有非常不同的值,包括環繞相鄰像素,就像紋理是平鋪的一樣。假設您有一個渲染像素的函數
,在 x 中的小變化導致 y 中的小變化, x 中的大變化導致 y 中的大變化。
當為 x 輸入非常不同的鄰居值時,也會為 y 輸出非常不同的鄰居值,從而使渲染結果具有藍色噪波錯誤模式。除非像素渲染函數是散列函數,否則此假設通常適用于幾何體邊或著色不連續。
還值得注意的是,時空藍色噪聲中的每個像素都是隨時間推移的漸進藍色噪聲序列,但從序列中的任何一點開始都是漸進的。這可以在查看 DFT 時看到,并記住傅里葉變換假設被變換序列的無限重復。
藍色噪波中沒有會扭曲頻率內容的接縫。這意味著,當使用 TAA 時,每個像素在不同的時間線上拋出其歷史記錄,當拒絕歷史記錄時,每個像素立即處于良好的漸進采樣序列上,而不是處于較差的序列上,直到序列重新啟動,這在其他采樣策略中很常見。這樣,時空藍色噪聲中的每個像素都是環形漸進的。
值得一提的是,在 TAA 下運動的像素失去了時間上的好處,我們的噪聲就如同純粹的空間藍色噪聲。然而,在一瞬間仍然是偶數的像素獲得了時間穩定性和較低的誤差,當它們再次運動時,這將由 TAA 攜帶。在這些情況下,我們的噪聲并不比空間藍色噪聲差,因此應始終使用它,以在可用的情況下獲得好處,并在其他情況下不會更差。
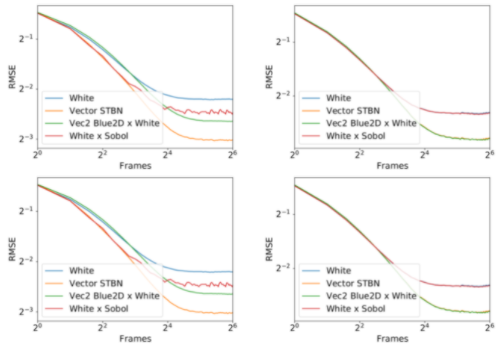
圖 1a 所有像素靜止時光線跟蹤 AO 的收斂速度
圖 1b 所有像素運動時光線跟蹤 AO 的收斂速度
藍色噪聲去噪
由于數字信號處理的原因,藍色噪聲比白色噪聲更容易從圖像中去除。白噪聲在所有頻率中具有隨機化,而藍噪聲僅在高頻中具有隨機化。
模糊(如長方體濾波器或高斯模糊)是一種低通濾波器,這意味著它可以去除高頻,但可以保持低頻。
當白噪聲模糊時,由于低通濾波器的低頻隨機化,它會變成噪聲斑點。
當藍色噪聲模糊時,高頻噪聲消失,圖像的低頻部分保持不變。
藍色噪聲在其創建過程中使用高斯能量函數,因此經過優化,可以通過高斯模糊去除。如果您使用高斯函數模糊藍色噪聲,并且看到噪聲斑點仍然存在,這意味著您必須在模糊中使用較大的 sigma ,因為藍色噪聲通過濾波器的頻率較低。在去除這些斑點和在去噪圖像中保留更多細節之間可能存在一種平衡。這取決于你的喜好。
圖 2 、 3 和 4 顯示了在使用原始噪聲和去噪時,藍色噪聲與白色噪聲的比較。
在圖 3 中,兩個圖像總共只有八種顏色,因為它們每個顏色通道只有 1 位。藍色噪聲 – 抖動圖像中有更多可識別和更精細的細節!
要了解為什么藍色噪聲比白色噪聲去噪效果更好,請在頻率空間中查看它們。通過卷積應用高斯模糊,這與頻率空間中的逐像素乘法相同。
如果你用高斯核頻率乘以藍色噪聲頻率,就什么都不剩了,而且全是黑色的;高斯模糊消除藍色噪聲。
如果你用高斯核頻率乘以白噪聲頻率,你會得到高斯核頻率的形狀(低頻),但它們是隨機的。這些是模糊白噪聲后留下的斑點。
圖 5 顯示了藍噪聲、白噪聲和高斯模糊核的頻率大小。

圖 5a 藍色噪音中出現的頻率 圖 5b 白噪聲中存在的頻率 圖 5c 高斯模糊低通濾波器中的頻率。
平鋪藍色噪音
由于沒有任何較大的比例(較低的頻率)內容,藍色噪聲平鋪良好。圖 6 顯示了這一點,但也顯示了藍色噪波平鋪在較低分辨率下變得更加明顯。這一點很重要,因為藍色噪波紋理通常在屏幕上平鋪,并在屏幕空間中使用。如果在使用藍色噪波時注意到平鋪,則應嘗試使用分辨率更高的藍色噪波紋理。

圖 6a 128 × 128 藍色噪波紋理平鋪 4 × 4 次 圖 6b 16 × 16 藍色噪波紋理平鋪 32 × 32 次
每像素獲取多個值
有時,您可能希望每個像素具有多個時空藍色噪波值,例如在渲染每個像素的多個采樣時。
一種方法是以固定的偏移量讀取紋理。例如,如果在(像素 x ,像素 y ) %textureSize 處讀取第一個值,則可能在(像素 x + 5 ,像素 y + 7 ) %textureSize 處讀取第二個值。這本質上為您提供了一個不相關的時空藍色噪波值,就像您有第二個正在讀取的時空藍色噪波紋理一樣。
之所以這樣做,是因為藍色噪波紋理僅在短距離內具有相關性。在長距離情況下,這些值是不相關的,如圖 7 所示。
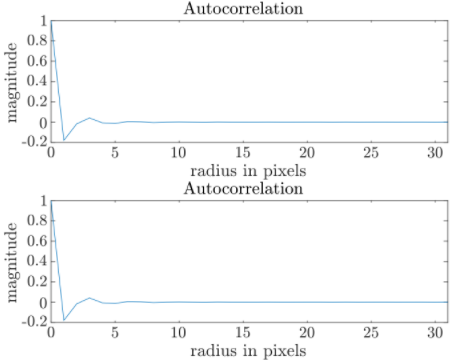
圖 7 。 64 × 64 藍色噪聲紋理的自相關。這表明,彼此相距約 7 個像素的像素可以具有相關性,而較大的距離是不相關的。
理想情況下,如果您想要 N 時空藍色噪波值,則應在彼此最大間隔的 N 偏移處讀取藍色噪波紋理。這樣做的一個好方法是有一個漸進的低差異序列,在其中插入隨機數索引,它會為您提供一個讀取紋理的偏移量。
我們已經非常成功地使用 馬丁·羅伯特的 R2 序列 插入索引,在[0 , 1]中獲得 2D 向量,然后乘以藍色噪波紋理大小以獲得要讀取的偏移量。
不過,還有另一種方法可以通過向每個像素添加秩 1 晶格來獲得每個像素的多個值。這樣做時,它類似于晶格上的 Cranley-Patterson 旋轉,但使用藍色噪聲而不是白色噪聲。
對于標量藍色噪聲,我們使用黃金比率或二的平方根得到了很好的結果。
對于非單位 vec2 藍色噪聲,我們使用 Martin Robert 的 R2 序列得到了很好的結果。
實際上,您可以使用相同的方法將 2D 藍色噪波紋理轉換為時空藍色噪波,但在該過程中會丟失一些質量。有關更多信息,請參閱 SIGGRAPH 2021 年關于此方法的論文 使用藍色噪聲誤差分布構建屏幕空間采樣器時的經驗教訓和改進 。
這種方法有時比時空藍噪聲收斂得更好,但誤差圖更不穩定,使其時間穩定性降低,并破壞藍噪聲頻譜。圖 8 顯示了頻率損傷,圖 8 顯示了一些收斂行為。有關收斂特性的更多信息,請參閱本文后面的簡單函數收斂部分。

圖 8 。黃金比例動畫藍色噪聲(頂部)和時空藍色噪聲(底部)的頻率構成。黃金比例動畫藍色噪波在不同幀上具有不均勻的頻率構成,這導致渲染在時間上不如時空藍色噪波穩定。
圖 9 顯示了將真實矢量時空藍色噪聲與 R2 低差異序列進行比較的圖表, R2 低差異序列使用單個矢量藍色噪聲紋理進行 Cransley-Patterson 旋轉。
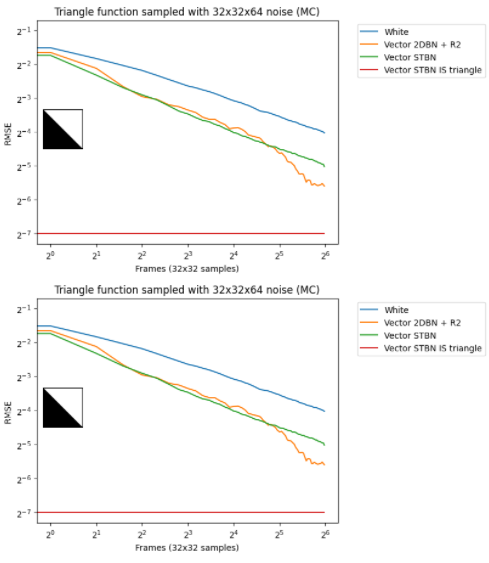
圖 9 。各種噪聲類型的收斂速度。白噪聲最差,重要采樣時空藍噪聲最好。在中間,從 2D 藍色噪聲開始的秩 1 晶格可以比均勻時空藍噪聲更好,但也更不穩定,并且在空間上破壞噪聲。
這兩種方法是其他方法之前設置藍色噪波動畫的方式。藍色噪波紋理在每幀上偏移,這使其在空間上為藍色噪波,在時間上為白色噪波,或者在低差異序列中播種藍色噪波值,使其在空間上為損壞的藍色噪波,但在時間上為良好的收斂序列。
通過曲線反演生成矢量值時空藍噪聲
如果你有一個標量時空藍色噪聲紋理,你可以把它通過一個倒置的莫頓或希爾伯特曲線,使它成為一個向量值時空藍色噪聲紋理。我們用希爾伯特曲線得到了更好的結果。雖然這些紋理的表現不如其他制造時空藍色噪聲的方法,但速度要快得多,甚至可以實時完成(圖 10 )。
這種方法的一個有趣之處是,我們發現它可以很好地處理各種抖動掩模或其他標量值(灰度)噪聲模式:拜耳矩陣 交錯梯度噪聲 ,甚至是樣式化的噪聲模式。
在所有這些情況下,當在渲染中使用向量時,會導致錯誤模式,這些錯誤模式采用源紋理的特性和外觀。這對于樣式化的噪波渲染可能很有趣,但也意味著將來,如果發現其他標量采樣遮罩,則可以使用此方法將它們轉換為具有相同屬性的向量值遮罩。
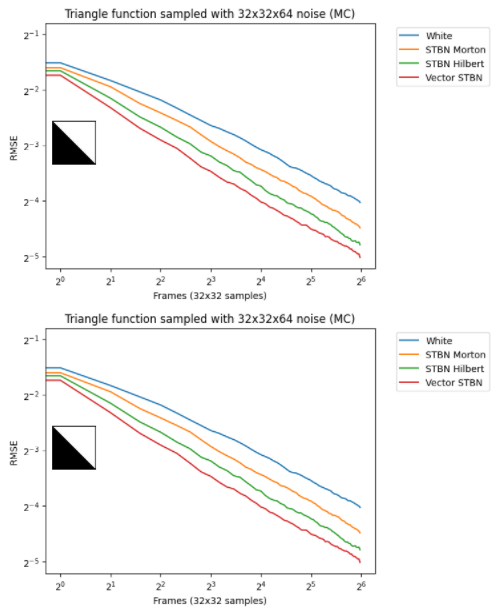
圖 10 。曲線反演可以產生比白噪聲更好的矢量值時空藍噪聲,但不如改進的 BNDS 算法產生的矢量值藍噪聲。
分層
只有在下列條件成立時,向量值時空藍色噪聲的能量函數才能修改為返回非零:
像素來自相同的切片(相同的 z 值)
交換中涉及的像素的時間直方圖不會變差
如果你這樣做,你最終會得到在空間上呈藍色,但隨著時間分層的噪音;分層順序是隨機的。因為分層不是漸進的,所以在采集所有樣本之前,它不會很好地收斂,但在這一點上效果很好(圖 11 )。
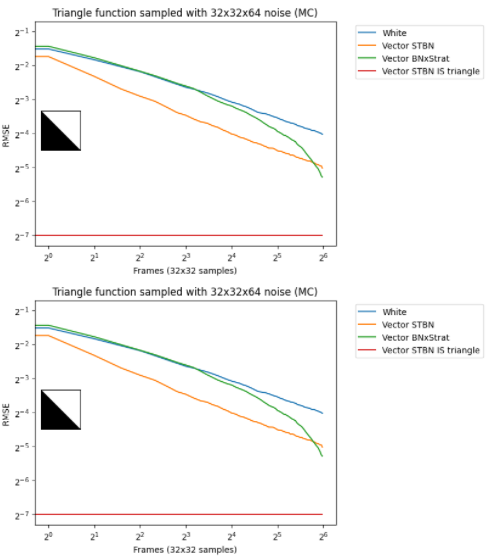
圖 11 。可以使用改進的 BNDS 算法產生在空間上呈藍色且隨時間分層的噪聲。收斂圖顯示它是非漸進的,但當所有樣本都被采集時,它的性能相當好。
高維藍噪聲
產生時空藍色噪聲的算法并不局限于 3D 。雖然到目前為止,我們還沒有找到這些算法的使用案例,但這些算法可以進行簡單的修改,以產生各種高維的藍色噪聲。如果時空藍色噪聲是 2Dx1D ,因為它在 XY 上是 2D 藍色噪聲,在 Z 上是 1D 藍色噪聲,圖 12 顯示了 4D 藍色噪聲的頻率大小,分別是 2Dx2D 和 2Dx1Dx1D ,尺寸為 64x64x16x16 。

圖 12 。 2Dx2D 和 2Dx1Dx1D 四維藍色噪聲在二維平面投影上的頻率構成。紋理為 64x64x16x16 。
點集
使用 void 和 cluster 算法生成的藍色噪波紋理可以閾值化為一個百分比值。許多像素在閾值化后存活下來,它們是藍色噪聲分布的。我們的標量值時空藍噪聲紋理具有相同的屬性,并產生時空藍噪聲點集。圖 13 顯示了標量時空藍色噪聲紋理的閾值點,以及這些閾值點的頻率振幅。

圖 13 。對時空藍色噪波紋理設置閾值,以生成時空藍色噪波點集。
這些點集使得每一幀的像素都以令人愉悅的空間藍色噪聲的方式分布,但每一幀也會得到不同的點集。這意味著,與白噪波或其他動畫藍噪波方法相比,隨著時間的推移,您可以獲得更多獨特的像素。圖 14 顯示了圖像的五幀累積樣本,使用重要性圖作為每像素藍色噪聲閾值。我們的噪波以最快的速度對最獨特的像素進行采樣,同時在空間上也提供了一個漂亮的藍色噪波圖案。

圖 14 。五幀累積樣本,使用重要性圖對每幀圖像進行隨機采樣。時空藍色噪聲以最快的速度對最獨特的像素進行采樣,從而在每一幀中提供最大數量的新信息。
單函數收斂
在本節中,我們將討論使用常見噪聲類型的簡單函數在蒙特卡羅積分和指數移動平均下的收斂性,以模擬 TAA 。
標量蒙特卡羅積分
圖 15 顯示了 Monte Carlo 積分下的收斂速度,就像您在每像素采集多個樣本時所做的一樣。 HB LDBN 來自 一種低偏差取樣器,將蒙特卡羅誤差作為藍色噪聲分布在屏幕空間中 。雖然低差異序列可以比 STBN 做得更好,但它在時間上更穩定,并且由于在空間上是藍色噪聲而產生良好的感知誤差。 STBN 偏移量 1 / 3 表明,如果從序列中的任意位置啟動 STBN ,它仍然保持良好的收斂特性。這表明 STBN 是環向漸進的。
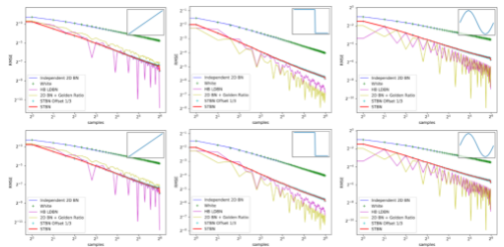
圖 15 。在蒙特卡羅積分下使用各種類型的噪聲進行標量函數收斂。時空藍噪聲并不總是最佳收斂,但它確實比白噪聲收斂得更好,并且在時間上是穩定的。
標量指數移動平均
圖 16 顯示了指數移動平均下的收斂速度。指數移動平均值以 0.1 的值從上一個值線性插值到下一個值。這模擬了無重投影或鄰域采樣拒絕的 TAA 。

圖 16 。利用指數移動平均下各種類型噪聲的標量函數收斂性來模擬 TAA 。時空藍色噪聲并不總是最佳收斂,但它確實比白色噪聲收斂得更好,并且在時間上是穩定的,同時也是環形漸進的,如與紅線幾乎匹配的藍色脈沖所示。
Vec2 蒙特卡羅積分
圖 17 顯示了蒙特卡羅積分下的收斂速度。標量 STBN 使用 R2 紋理偏移方法讀取此 2D 積分的兩個標量值。因此,它在階躍函數(最終是一個一維問題)和雙線性函數(最終是一個軸對齊問題)中的性能優于向量 STBN 。重要抽樣有任何錯誤的原因都是由于向量和 PDF 值的離散化。
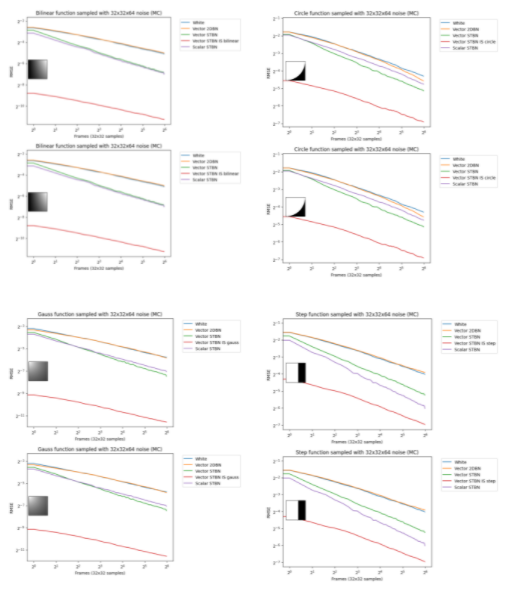
圖 17 。使用 vec2 噪聲的 vec2 函數的 Monte Carlo 收斂速度
指數移動平均數
圖 18 顯示了 EMA 下的收斂。指數移動平均值以 0.1 的值從上一個值線性插值到下一個值。這模擬了無重投影或鄰域采樣拒絕的 TAA 。
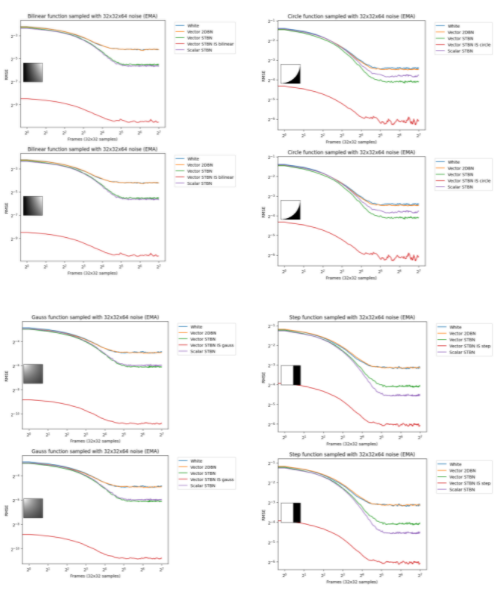
圖 18 。使用 vec2 噪聲的 vec2 函數的指數移動平均收斂速度。這將模擬 TAA 下的行為
結論
雖然藍色噪聲采樣點近年來取得了進步,但幾十年來,藍色噪聲紋理似乎在很大程度上被忽略了。如圖所示,時空藍色噪聲紋理對于實時渲染具有幾個理想的特性,在實時渲染中只能提供較低的采樣數:良好的空間誤差模式、更好的時間穩定性和收斂性,以及環形漸進性,僅舉幾例。
我們認為,這些紋理只是開始,因為還有其他幾種改進采樣紋理的可能性,無論它們是基于藍色噪波的、混合的還是完全其他的。
但值得注意的是,還有其他方法可以在樣本數最低的情況下獲得很好的結果。例如, NVIDIA RTXDI 也適用于這種情況,但使用不同的方法。
關于作者
Alan Wolfe 最初是一名自學成才的游戲編程愛好者,擁有超過 20 年的游戲開發經驗,擁有包括《星際爭霸 2 》、《風暴英雄》、《高譚市冒名頂替者》、《線騎士》和《瘋狂扭曲的陰影星球》在內的多部游戲。 Alan 對藍色噪音和其他隨機渲染方法有著不健康的迷戀。
Nathan Morrical 是博士。猶他大學的學生,來自NVIDIA OpTix 團隊的實習生和皮克斯的 RenderMan 集團,以及科學計算和成像研究所( SCI )的現任成員。他的研究興趣包括高性能光線跟蹤框架和計算、科學數據可視化、計算幾何和實時光線跟蹤。在加入 SCI 之前, Nate 在愛達荷州立大學獲得了計算機科學學士學位,在那里他研究了交互式計算機圖形學和計算幾何。
Tomas Akenine-Moller 是NVIDIA 杰出的研究科學家,目前正在休假,他是隆德大學計算機圖形學教授。托馬斯與人合著 Real-Time Rendering 、 浸入線性代數 并共同編輯 射線追蹤寶石 I 。
Ravi Ramamoorthi 是 Nvidia 的一名研究顧問,他是圣地亞哥加利福尼亞大學的教授,他擔任 Ronald L.Graham 計算機科學系的主席,也是 UCSD 視覺計算中心的創始主任。
審核編輯:郭婷
-
噪聲
+關注
關注
13文章
1121瀏覽量
47400 -
NVIDIA
+關注
關注
14文章
4981瀏覽量
102997
發布評論請先 登錄
相關推薦
維智科技亮相首屆時空智能國際學術研討會
低噪聲紋波探頭測量應用指南
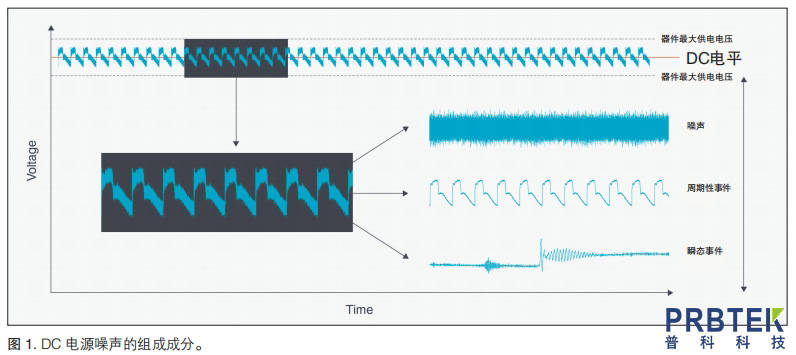
調試PCM3500E,DAC輸出噪聲紋波峰峰值居然高達600mV,為什么?
RT-Thread攜手進迭時空:共建RISC-V實時計算生態

VIVERSE 推行實時3D渲染: 探索Polygon Streaming技術力量與應用
CPU渲染和GPU渲染優劣分析

烘焙vs渲染:3D模型制作中的效率與質量之爭

HarmonyOS實戰開發-合理選擇條件渲染和顯隱控制
【RTC程序設計:實時音視頻權威指南】音頻采集與渲染
【RTC程序設計:實時音視頻權威指南】視頻采集與渲染
測電源噪聲紋波時為什么選無源探頭





 使用時空藍色噪聲紋理實時渲染二
使用時空藍色噪聲紋理實時渲染二










評論